The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
12MR2
MR2
72MR2
32MR2
The correct Answer is:d
To find the moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc, we can follow these steps:
Step 1: Identify the Moment of Inertia about the Center of Mass
The moment of inertia Icm of a uniform circular disc about an axis passing through its center and perpendicular to the plane of the disc is given by the formula:
Icm=12MR2
Step 2: Use the Parallel Axis Theorem
To find the moment of inertia about an axis that is parallel to the one through the center of mass but located at the edge of the disc, we can use the Parallel Axis Theorem. The theorem states:
I=Icm+Md2
where d is the distance between the two axes. In this case, the distance d is equal to the radius R of the disc.
Step 3: Substitute the Values
Substituting the values into the equation:
I=Icm+MR2
I=12MR2+MR2
Step 4: Combine the Terms
Now, we can combine the terms:
I=12MR2+22MR2=32MR2
Step 5: Final Result
Thus, the moment of inertia of the uniform circular disc about the axis passing from the edge of the disc and normal to the disc is:
I=32MR2
Summary
The final answer is:
32MR2
The moment of inertia Icm of a uniform circular disc about an axis passing through its center and perpendicular to the plane of the disc is given by the formula:
Icm=12MR2
To find the moment of inertia about an axis that is parallel to the one through the center of mass but located at the edge of the disc, we can use the Parallel Axis Theorem. The theorem states:
I=Icm+Md2
where d is the distance between the two axes. In this case, the distance d is equal to the radius R of the disc.
Substituting the values into the equation:
I=Icm+MR2
I=12MR2+MR2
Now, we can combine the terms:
I=12MR2+22MR2=32MR2
Thus, the moment of inertia of the uniform circular disc about the axis passing from the edge of the disc and normal to the disc is:
I=32MR2
The final answer is:
32MR2
Similar Questions
Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through -
View SolutionCalculate the moment of inertia of a.unifprm disc of mass 0.4 kg and radius 0.1m about an axis passing through its edge and perpendicular to the plane of die disc ?
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionThe moment of inertia of a disc of mass M and radius R about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
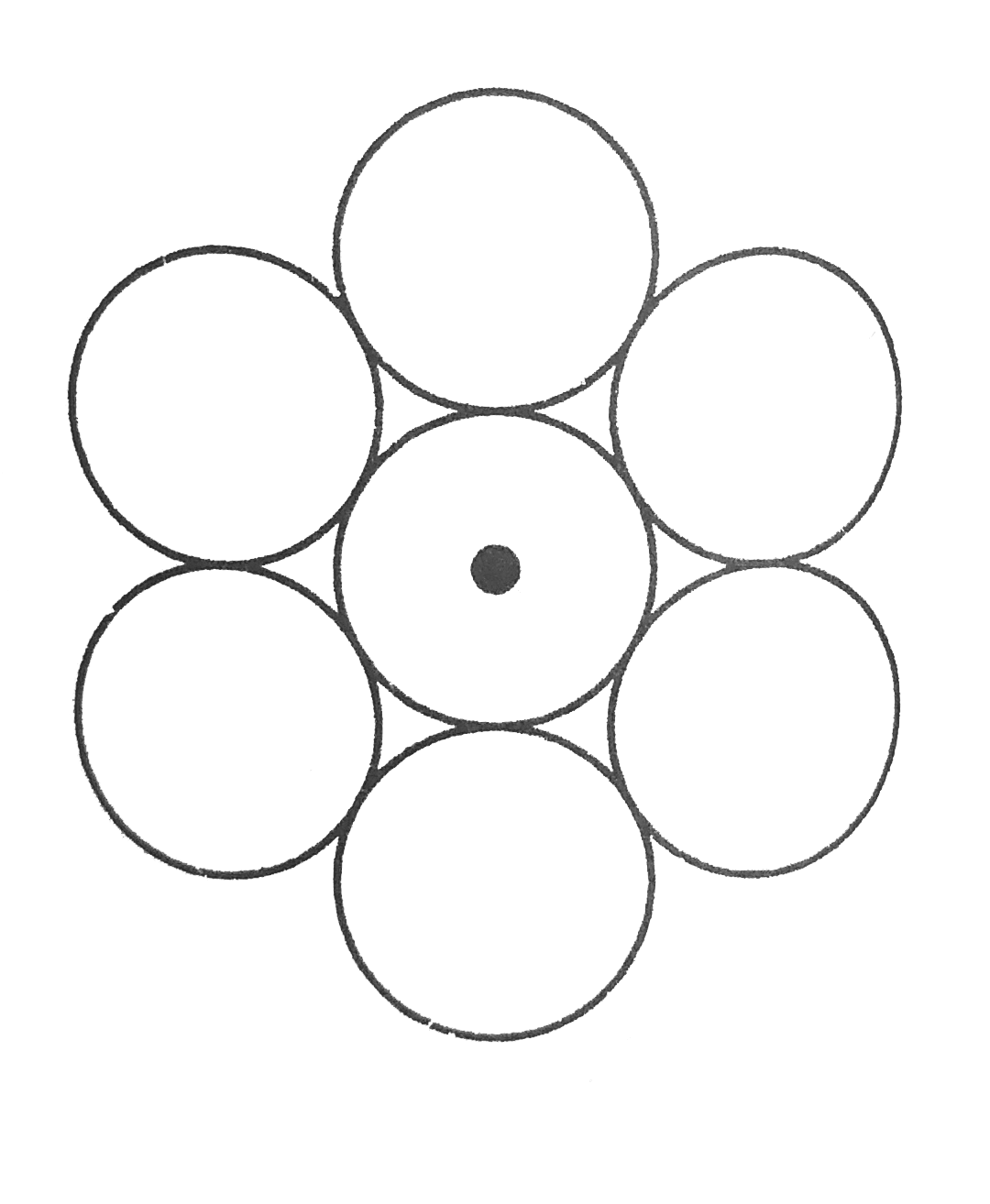
View SolutionSeven identical disc are arranged in a hexagonal, planar pattern so as to touch each neighbour, as shown in the figure. Each disc has mass m and radius r. What is the moment of inertia of the system of seven disks about an axis passing through the centre of central disk and normal to plane of all disks ?
 .
.
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
View Solution