A circular disc is to be made by using iron and aluminium, so that it acquires maximum moment of inertia about its geometrical axis. It is possible with
aluminimum is at the interior and iron surrounds it
iron is at the interior and aluminimum surrrounds it
aluminium and iron layers are in alternate order
sheet of iron is used at both external surfaces and aluminium sheet as inner material
The correct Answer is:a
To solve the problem of maximizing the moment of inertia of a circular disc made from iron and aluminum, we can follow these steps:
1. Understand the Moment of Inertia:
The moment of inertia (I) of a body about an axis is given by the formula:
I=∑mir2i
where mi is the mass of each particle and ri is the distance from the axis of rotation.
2. Identify the Materials:
We have two materials: iron and aluminum. We need to consider their densities and how they will be arranged in the disc.
3. Compare Densities:
Iron is denser than aluminum. This means that for the same volume, iron will have a greater mass than aluminum.
4. Maximize Moment of Inertia:
To maximize the moment of inertia, we want to place the heavier material (iron) at a greater distance from the axis of rotation. This is because the moment of inertia increases with the square of the distance from the axis (r2).
5. Arrangement of Materials:
To achieve maximum moment of inertia, we should place aluminum (the lighter material) closer to the center and iron (the heavier material) further away from the center.
6. Conclusion:
Therefore, the correct arrangement is to have aluminum in the interior and iron surrounding it.
Final Answer:
The correct option is that aluminum is in the interior and iron surrounds it.
The moment of inertia (I) of a body about an axis is given by the formula:
I=∑mir2i
where mi is the mass of each particle and ri is the distance from the axis of rotation.
We have two materials: iron and aluminum. We need to consider their densities and how they will be arranged in the disc.
Iron is denser than aluminum. This means that for the same volume, iron will have a greater mass than aluminum.
To maximize the moment of inertia, we want to place the heavier material (iron) at a greater distance from the axis of rotation. This is because the moment of inertia increases with the square of the distance from the axis (r2).
To achieve maximum moment of inertia, we should place aluminum (the lighter material) closer to the center and iron (the heavier material) further away from the center.
Therefore, the correct arrangement is to have aluminum in the interior and iron surrounding it.
The correct option is that aluminum is in the interior and iron surrounds it.
Similar Questions
The rotational inertia of a disc about its geometrical axis does not depend upon its
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View Solution(A) : Two circular discs of equal masses and thickness made of different material, will have same moment of inertia about their central axes of rotation.
(R ) : Moment of inertia depends upon the distribution of mass in the body.View SolutionAbout which axis moment of inertia in the given triangular lamina is maximum?
 View Solution
View SolutionA circular disc of radius R and thickness R6 has moment of inertia I about its axis. If it is melted and casted into a solid sphere then what will be its moment of inertia, about its diametric axis?
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
View SolutionA circular disc of radius R and thickness R6 has moment of inertia about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
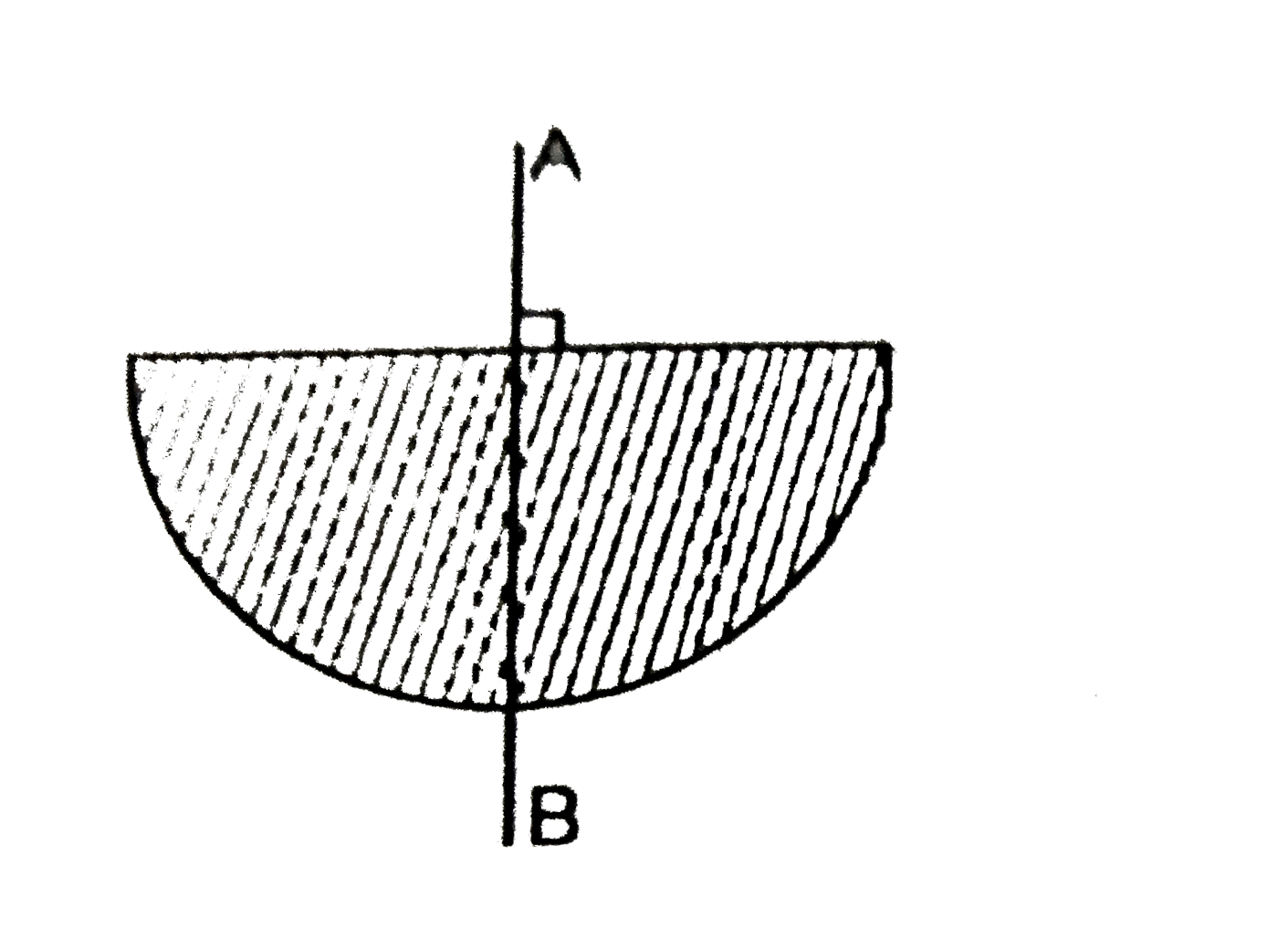 View Solution
View Solution

