Moment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
The correct Answer is:A
To find the moment of inertia of a cylindrical shell of mass M, radius R, and length L about its geometrical axis, we can follow these steps:
Step 1: Understanding the Geometry
We have a cylindrical shell with:
- Mass M
- Radius R
- Length L
The moment of inertia I about the geometrical axis (the axis along the length of the cylinder) needs to be determined.
Step 2: Consider a Differential Element
Consider a thin strip of the cylindrical shell at a distance R from the axis. This strip has a small mass dm and length L. The moment of inertia dI of this differential strip about the axis is given by the formula:
dI=R2dm
Step 3: Integrate Over the Entire Mass
To find the total moment of inertia I, we need to integrate dI over the entire mass M of the cylindrical shell. Since the radius R is constant for the entire shell, we can take R2 out of the integral:
I=∫dI=R2∫dm
Step 4: Evaluate the Integral
The integral ∫dm gives us the total mass M of the cylindrical shell:
I=R2⋅M
Step 5: Final Result
Thus, the moment of inertia I of the cylindrical shell about its geometrical axis is:
I=MR2
Conclusion
The correct answer is MR2, which corresponds to option 1.
---
We have a cylindrical shell with:
- Mass M
- Radius R
- Length L
Consider a thin strip of the cylindrical shell at a distance R from the axis. This strip has a small mass dm and length L. The moment of inertia dI of this differential strip about the axis is given by the formula:
dI=R2dm
To find the total moment of inertia I, we need to integrate dI over the entire mass M of the cylindrical shell. Since the radius R is constant for the entire shell, we can take R2 out of the integral:
I=∫dI=R2∫dm
The integral ∫dm gives us the total mass M of the cylindrical shell:
I=R2⋅M
Thus, the moment of inertia I of the cylindrical shell about its geometrical axis is:
I=MR2
The correct answer is MR2, which corresponds to option 1.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
Find the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View SolutionMoment of inertia of a circular wire of mass M and radius R about its diameter is
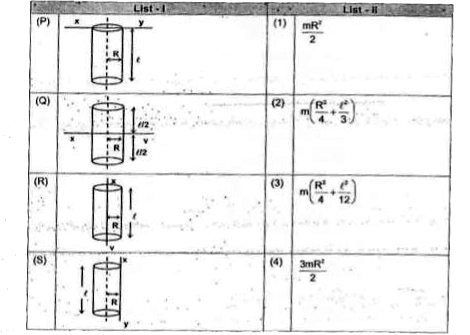
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionThe moment of inertia of a spherical shell and a hemispherical shell of same mass and radius about a tangential axis, passing through P will be

View SolutionThe moment of inertia of a door of mass m, length 2l and width l about its longer side is.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

View SolutionThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View Solution
