In SHM restoring force is F=−kx, where k is force constant, x is displacement and a is amplitude of motion, then total energy depends upon
k, a and m
k, x,m
k, a
k,x
The correct Answer is:C
To solve the problem of determining what the total energy in Simple Harmonic Motion (SHM) depends upon, we will follow these steps:
Step 1: Understand the Restoring Force
The restoring force in SHM is given by the equation:
F=−kx
where k is the force constant and x is the displacement from the equilibrium position.
Step 2: Identify Kinetic Energy
The kinetic energy (KE) of a particle in SHM can be expressed as:
KE=12mv2
where m is the mass of the particle and v is its velocity.
Step 3: Express Velocity in SHM
For a particle performing SHM, the velocity can be expressed as:
v=ω√A2−x2
where ω is the angular frequency and A is the amplitude of motion.
Step 4: Substitute Velocity into Kinetic Energy
Substituting the expression for v into the kinetic energy formula gives:
KE=12m(ω√A2−x2)2
KE=12mω2(A2−x2)
Step 5: Identify Potential Energy
The potential energy (PE) in SHM is given by:
PE=12kx2
Step 6: Relate k to ω
We can relate k to ω using the formula:
ω2=km
Thus, we can substitute k as k=mω2.
Step 7: Substitute Potential Energy
Substituting k into the potential energy formula gives:
PE=12(mω2)x2
Step 8: Calculate Total Energy
The total energy E in SHM is the sum of kinetic and potential energy:
E=KE+PE
Substituting the expressions for KE and PE:
E=12mω2(A2−x2)+12(mω2)x2
E=12mω2A2
Step 9: Final Expression for Total Energy
Thus, the total energy in SHM can be expressed as:
E=12mω2A2
Step 10: Identify Dependencies
From the final expression, we can see that the total energy depends on:
- Mass m
- Angular frequency ω
- Amplitude A
Step 11: Replace ω with k
Since ω2=km, we can also express total energy in terms of k:
E=12(km)mA2=12kA2
Conclusion
Thus, the total energy in SHM depends on the force constant k and the amplitude A.
---
The restoring force in SHM is given by the equation:
F=−kx
where k is the force constant and x is the displacement from the equilibrium position.
The kinetic energy (KE) of a particle in SHM can be expressed as:
KE=12mv2
where m is the mass of the particle and v is its velocity.
For a particle performing SHM, the velocity can be expressed as:
v=ω√A2−x2
where ω is the angular frequency and A is the amplitude of motion.
Substituting the expression for v into the kinetic energy formula gives:
KE=12m(ω√A2−x2)2
KE=12mω2(A2−x2)
The potential energy (PE) in SHM is given by:
PE=12kx2
We can relate k to ω using the formula:
ω2=km
Thus, we can substitute k as k=mω2.
Substituting k into the potential energy formula gives:
PE=12(mω2)x2
The total energy E in SHM is the sum of kinetic and potential energy:
E=KE+PE
Substituting the expressions for KE and PE:
E=12mω2(A2−x2)+12(mω2)x2
E=12mω2A2
Thus, the total energy in SHM can be expressed as:
E=12mω2A2
From the final expression, we can see that the total energy depends on:
- Mass m
- Angular frequency ω
- Amplitude A
Since ω2=km, we can also express total energy in terms of k:
E=12(km)mA2=12kA2
Thus, the total energy in SHM depends on the force constant k and the amplitude A.
Similar Questions
The spring force is given by F=−kx, here k is a constant and x is the deformation of spring. The F−x graph is
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View Solution
Knowledge Check
If x−4 is a factor of x2−kx+2k, where k is a constant, what is the value of k?
A−4B4C8D12
In a simple harmonic motion, when the displacement is one-half the amplitude, what fraction of the total energy is kinetic ?
View SolutionThe total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
View SolutionThe potential energy of a particle execuring S.H.M. is 5 J, when its displacement is half of amplitude. The total energy of the particle be
View SolutionAn object of mass m is attached to a spring. The restroing force of the spring is F=−λx3, where x is the displacement. The oscillation period depends on the mass, lmabd and oscillation amplitude. Suppose the object is initially at rest. If the initial displacement is D then its period is τ. If the initial displacement is 2D, find the period.
View Solution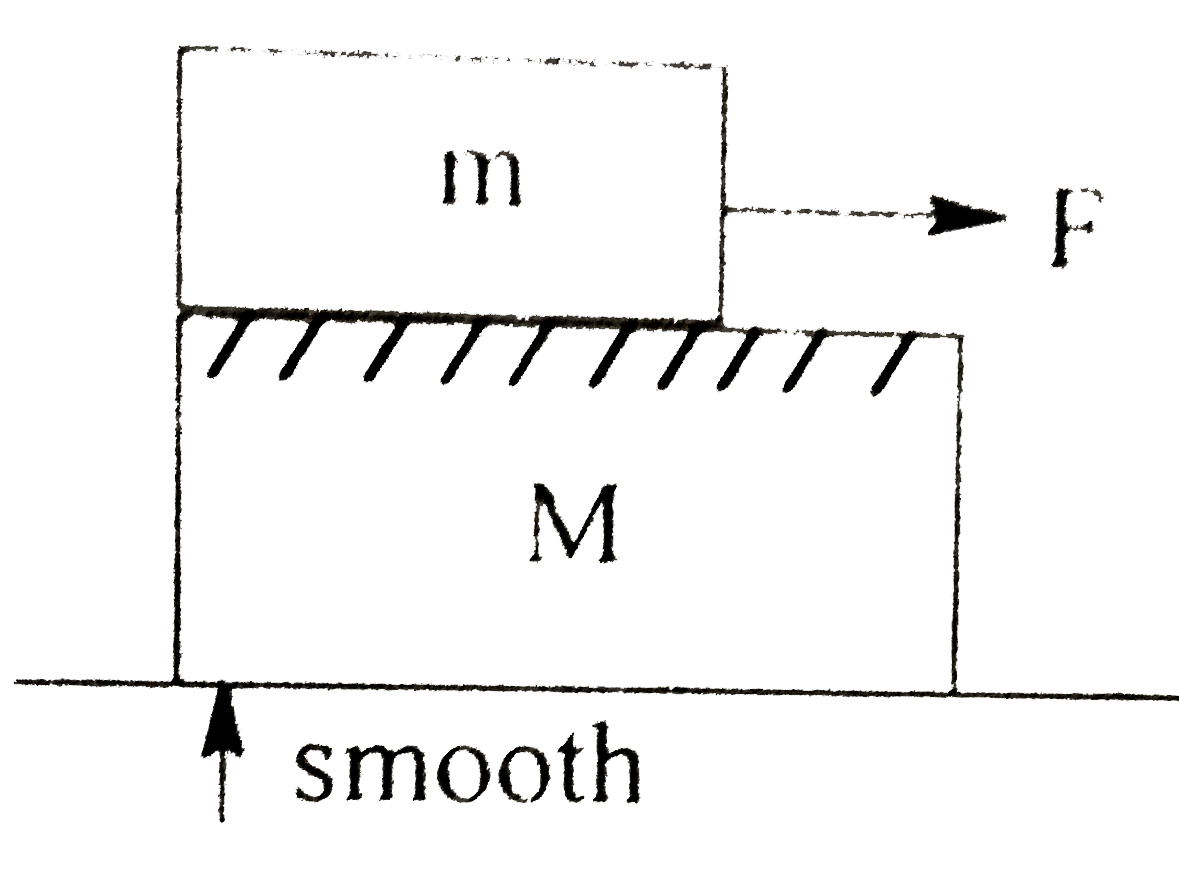
A plank having mass M is placed on smooth horizontal surface. Block of mass m is placed on it coefficient of friction between block and plank is μ0+kx, where k is constant and x is relative displacement between block and plank. A force F is applied on block where F=at, where a=10 t is in second. find t0 when relative motion will occur between block and plank.
View SolutionConsider a spring that exerts the following restoring force :
F=−kx for x≥0
F=−4kx for x<0
A mass m on a frictionless surface is attached to the spring displaced to x=A by strectching the spring and released :
View SolutionA particle moves under the force F(x)=(x2−6x)N, where x is in metres. For small displacements from the origin what is the force constant in the simple harmonic motion approximation ?
View Solution
