A charged wire is bent in the form of a semicircular arc of radius a. If charge per unit length is λ coulomb/metre, the electric field at the centre O is
λ2πa2ε0
λ4π2ε0a
λ2πε0a
zero
The correct Answer is:C
To find the electric field at the center O of a semicircular arc of radius a with a uniform charge density λ, we can follow these steps:
1. Understand the Geometry:
We have a semicircular arc with radius a. The total charge is distributed uniformly along the arc.
2. Consider a Small Element:
Take a small charge element dq on the arc. The length of this small element is dl, which can be expressed in terms of the angle dθ as:
dl=adθ
Therefore, the charge dq can be expressed as:
dq=λdl=λadθ
3. Electric Field Contribution:
The electric field dE due to the charge element dq at the center O can be calculated using Coulomb's law:
dE=kdqa2=kλadθa2=kλdθa
where k=14πϵ0.
4. Components of Electric Field:
The electric field dE can be resolved into two components:
- The radial component dEcosθ (which will cancel out due to symmetry).
- The vertical component dEsinθ (which will add up).
5. Calculate the Vertical Component:
The vertical component of the electric field dEy is given by:
dEy=dEsinθ=kλasinθdθ
6. Integrate Over the Semicircular Arc:
We need to integrate dEy from θ=0 to θ=π:
Ey=∫π0dEy=∫π0kλasinθdθ
The integral of sinθ is:
∫sinθdθ=−cosθ
Evaluating from 0 to π:
Ey=kλa(−cosθ)π0=kλa(−(−1−1))=kλa⋅2=2kλa
7. Substituting for k:
Substitute k=14πϵ0:
Ey=2⋅14πϵ0λa=λ2πϵ0a
Final Result:
The electric field at the center O of the semicircular arc is:
E=λ2πϵ0a
We have a semicircular arc with radius a. The total charge is distributed uniformly along the arc.
Take a small charge element dq on the arc. The length of this small element is dl, which can be expressed in terms of the angle dθ as:
dl=adθ
Therefore, the charge dq can be expressed as:
dq=λdl=λadθ
The electric field dE due to the charge element dq at the center O can be calculated using Coulomb's law:
dE=kdqa2=kλadθa2=kλdθa
where k=14πϵ0.
The electric field dE can be resolved into two components:
- The radial component dEcosθ (which will cancel out due to symmetry).
- The vertical component dEsinθ (which will add up).
The vertical component of the electric field dEy is given by:
dEy=dEsinθ=kλasinθdθ
We need to integrate dEy from θ=0 to θ=π:
Ey=∫π0dEy=∫π0kλasinθdθ
The integral of sinθ is:
∫sinθdθ=−cosθ
Evaluating from 0 to π:
Ey=kλa(−cosθ)π0=kλa(−(−1−1))=kλa⋅2=2kλa
Substitute k=14πϵ0:
Ey=2⋅14πϵ0λa=λ2πϵ0a
The electric field at the center O of the semicircular arc is:
E=λ2πϵ0a
Similar Questions
A wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionA wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
View SolutionA wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is

View SolutionThe linear charge density on upper half of semi-circular section of ring is λ and that at lower half is −λ. The direction of electric field at centre O of ring is :

View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionOn meter length of wires carriers a constant current. The wire is bent to from a circular loop. The magnetic field at the centre of this loop is B. The same is now bent to form a circular loop of smaller radius to have four turns in the loop. The magnetic field at the centre of this loop B. The same is now bent to form a circular loop of smaller radius of have four turns in the loop. The magnetic field at the centre of this new loop is
View SolutionThe charge per unit length of the four quadrant of the ring is 2λ,−2λ,λ and −λ respectively. The electric field at the centre is:
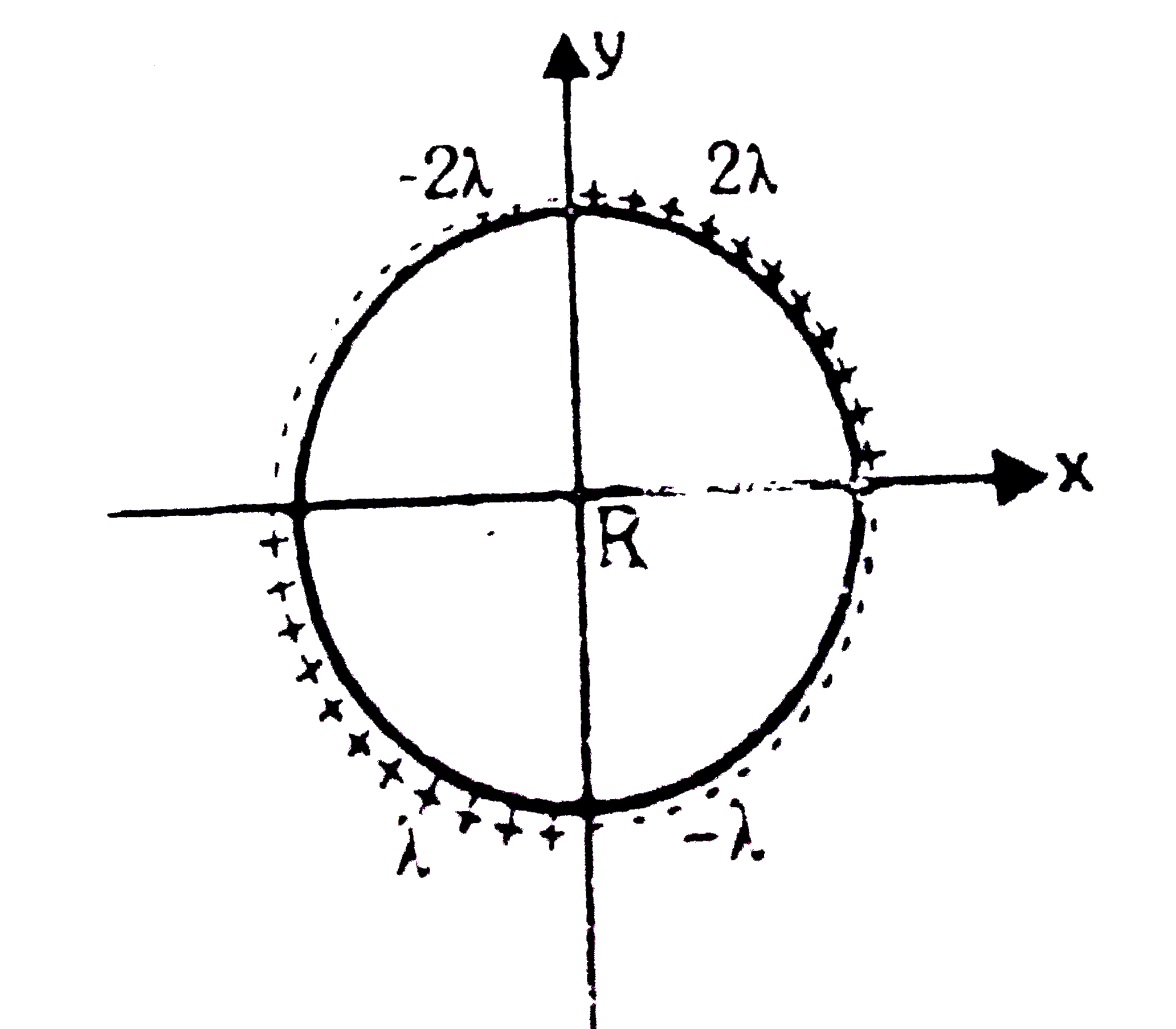
View SolutionA wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
View Solution
A small part of dl length is removed from a ring having charge per unit length λ. Find electric field at centre due to remaining ring.
View SolutionA wire bent in the form of a sector of radius r subtending an angle θ∘ at centre as shown in figure is carrying a current I. The magnetic field at O is :
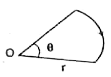
View Solution
