A student measures the terminal potential difference (V) of a cell (of emf ε and internal resistance r) as a function of the current (I) flowing through it. The slope and intercept of the graph between V and I, then respectively, equal
ε and −r
−r and ε
r and −ε
−ε and r
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the terminal potential difference V of a cell, its electromotive force ϵ, internal resistance r, and the current I flowing through it.
1. Understand the Relationship: According to the problem, we have a cell with an electromotive force ϵ and internal resistance r. The terminal potential difference V can be expressed in terms of ϵ, r, and I.
2. Apply Kirchhoff's Voltage Law (KVL): We can write the equation for the terminal potential difference as:
V=ϵ−I⋅r
This equation states that the terminal voltage V is equal to the emf ϵ minus the voltage drop across the internal resistance r due to the current I.
3. Identify the Form of the Equation: The equation V=ϵ−I⋅r can be rearranged to match the linear equation format y=mx+c, where:
- y is V
- m is the slope (which is −r)
- x is I
- c is the y-intercept (which is ϵ)
4. Determine the Slope: From the equation V=ϵ−I⋅r, we can see that the slope m is:
m=−r
5. Determine the Intercept: The y-intercept c from the equation is:
c=ϵ
Final Result:
- The slope of the graph between V and I is −r.
- The intercept of the graph is ϵ.
Conclusion:
The slope and intercept of the graph between V and I are respectively:
- Slope: −r
- Intercept: ϵ
V=ϵ−I⋅r
This equation states that the terminal voltage V is equal to the emf ϵ minus the voltage drop across the internal resistance r due to the current I.
- y is V
- m is the slope (which is −r)
- x is I
- c is the y-intercept (which is ϵ)
m=−r
c=ϵ
- The slope of the graph between V and I is −r.
- The intercept of the graph is ϵ.
The slope and intercept of the graph between V and I are respectively:
- Slope: −r
- Intercept: ϵ
Similar Questions
A cell of emf ε and internal resistance r is charged by a current I, then
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionHow are the potential difference (V), current (I) and resistance (R) related ?
View SolutionA cell of emf 'E' and internal resistance 'r' draws a current 'I'. Write the relation between terminal voltage 'V' in terms of E, I and r.
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
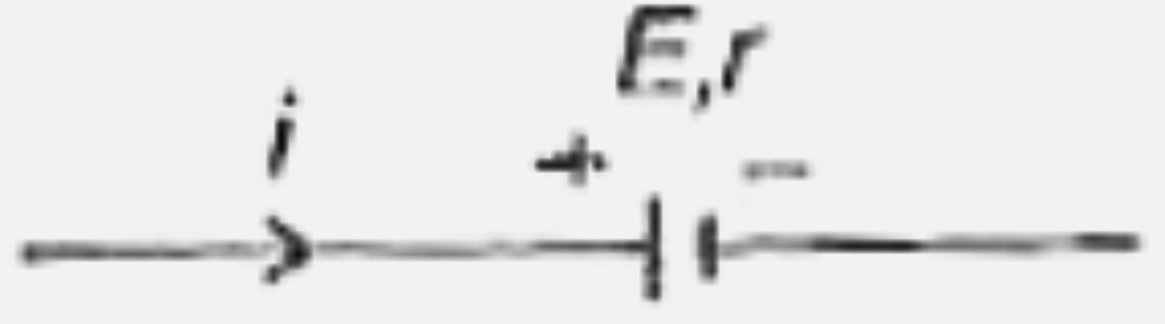
View SolutionAssertion: Terminal potential difference of a cell is always less than its emf.
Reason: Potential drop on internal resistance of cell increases terminal potential difference.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionDraw a graph of potential difference (V) versus current (I) for an ohmic resistor.
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View Solution