A cell can be balanced against 110cm and 100cm of potentiometer wire, respectively with and without being short circuited through a resistance of 10Ω. Its internal resistance is
1.0Ω
0.5Ω
2.0Ω
zero
The correct Answer is:A
To find the internal resistance of the cell, we can follow these steps:
Step 1: Understand the problem
We have a cell that can be balanced against two different lengths of a potentiometer wire: 110 cm when the cell is not short-circuited, and 100 cm when it is short-circuited through a resistance of 10 Ω.
Step 2: Set up the relationship
When the cell is connected to the potentiometer wire, the electromotive force (E) of the cell can be expressed in terms of the lengths of the wire (L1 and L2) and the resistances involved. The relationship can be given as:
E=k⋅L
where k is a constant of proportionality and L is the length of the wire.
Step 3: Define the lengths
Let:
- L1=110 cm (length when not short-circuited)
- L2=100 cm (length when short-circuited)
Step 4: Set up the equations
When the cell is not short-circuited:
E=k⋅110
When the cell is short-circuited through a resistance R=10Ω:
E−I⋅r=k⋅100
where r is the internal resistance of the cell and I is the current flowing through the circuit.
Step 5: Relate the two scenarios
From the first scenario:
E=k⋅110
From the second scenario:
E=k⋅100+I⋅r
Step 6: Express current in terms of resistance
Using Ohm's law, the current I can be expressed as:
I=ER+r
Substituting this into the second equation gives:
E=k⋅100+ER+r⋅r
Step 7: Substitute known values
Now, we can substitute R=10Ω into the equations. We also know that:
L1−L2L2=rR
Thus:
110−100100=r10
This simplifies to:
10100=r10
110=r10
Step 8: Solve for internal resistance r
Cross-multiplying gives:
r=1Ω
Final Result
The internal resistance of the cell is r=1Ω.
---
We have a cell that can be balanced against two different lengths of a potentiometer wire: 110 cm when the cell is not short-circuited, and 100 cm when it is short-circuited through a resistance of 10 Ω.
When the cell is connected to the potentiometer wire, the electromotive force (E) of the cell can be expressed in terms of the lengths of the wire (L1 and L2) and the resistances involved. The relationship can be given as:
E=k⋅L
where k is a constant of proportionality and L is the length of the wire.
Let:
- L1=110 cm (length when not short-circuited)
- L2=100 cm (length when short-circuited)
When the cell is not short-circuited:
E=k⋅110
When the cell is short-circuited through a resistance R=10Ω:
E−I⋅r=k⋅100
where r is the internal resistance of the cell and I is the current flowing through the circuit.
From the first scenario:
E=k⋅110
From the second scenario:
E=k⋅100+I⋅r
Using Ohm's law, the current I can be expressed as:
I=ER+r
Substituting this into the second equation gives:
E=k⋅100+ER+r⋅r
Now, we can substitute R=10Ω into the equations. We also know that:
L1−L2L2=rR
Thus:
110−100100=r10
This simplifies to:
10100=r10
110=r10
Cross-multiplying gives:
r=1Ω
The internal resistance of the cell is r=1Ω.
Similar Questions
A Daniel cell is balanced on 125cm length of a potentiometer wire. Now the cells is short-circuited by a resistance 2ohm and the balance is obtained at 100cm. The internal resistance of the Dainel cell is
View SolutionFor a cell of e.m.f. 2 V , a balance is obtained for 50 cm of the potentiometer wire. If the cell is shunted by a 2Ω resistor and the balance is obtained across 40 cm of the wire, then the internal resistance of the cell is
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionIn a potentiometer experiment, the galvanometer shows no deflection when a cell is connected across 60cm of the potentiometer wire. If the cell is shunted by a resistance of 6Ω, the balance is obtained across 50cm of the wire. The internal resistance of the cell is
View SolutionA 20 m long potentiometer wire has a resistance of 20 Ohm. It is connected in series with a battery of emf 3V and resistance of 10Ω. The internal resistance of cell is negligible. If the lenth can be read accurately up to 1 mm, the potentiometer can read voltage:
View Solution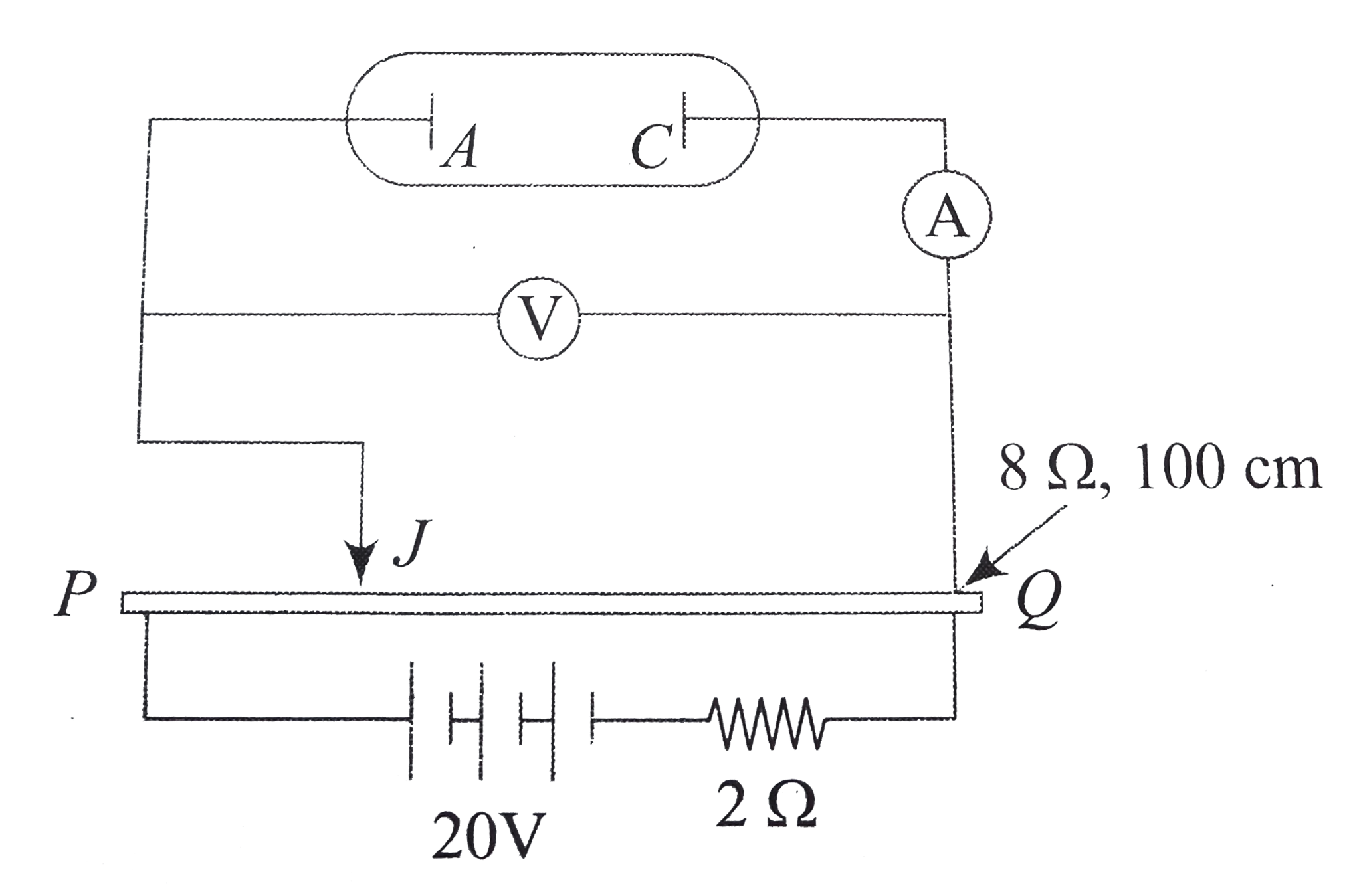
An experimental setup of verification of photoelectric effect is shown if Fig. The voltage across the electrodes is measured with the help of an ideal voltmeter, and which can be varied by moving jockey J on the potentiometer with wire. The battery used in potentiometer circuit is of 20 V and its internal resistance is 2Ω. The resistance of 100 cm long potentiometer wire is 8Ω.
The photocurrent is measured with the help of an ideal ammeter. Two plates of potassium oxide of area 50cm2 at separation 0.5mm are used in the vacuum tube. Photocurrent in the circuit is very small, so we can treat the potentiometer circuit as an independent circuit. The wavelength of various colors is as follows:
Q. It is found that ammeter current remains unchanged (2μA) even when the jockey is moved from the end P to the middle point of the potentiometer wire. Assuming that all the incident photons eject electrons and the power of the light incident is 4×10−6 W. Then, the color of the incident light is
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View SolutionA standerd cell emf 1.08Vis balance by the potential difference across 91cm of a meter long wire applied by a cell of emf 2V through a series resistor of resistance 2Ω. The internal resistance of the cell is zero. Find the resistance per unit length of the potentiometer wire.
View SolutionA 10m long potentiometer wire has a resistance of 20 ohm. It is connected in series with a battery of emf 3V and a resistance of 10Ω. The internal resistance of cell is negligible. If he length can be read accurately up 10 1mm, the potentiometer can read voltage.
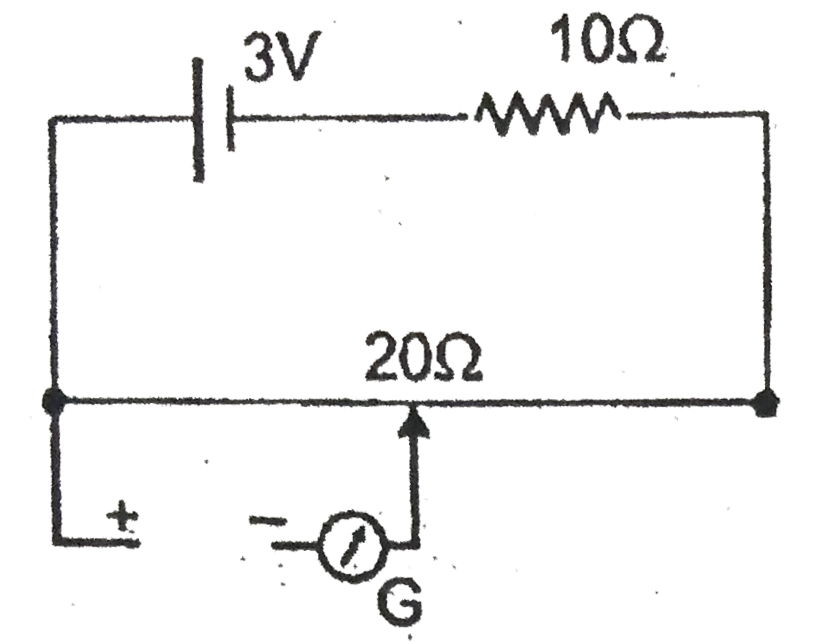
View Solution
