The internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
0.2Ω
0.5Ω
0.8Ω
1.0Ω
The correct Answer is:B
To find the internal resistance of a 2.1V cell that gives a current of 0.2A through a resistance of 10Ω, we can follow these steps:
1. Identify the known values:
- EMF of the cell (E) = 2.1V
- Current (I) = 0.2A
- External resistance (R) = 10Ω
2. Use Ohm's Law:
According to Ohm's Law, the total voltage (V) in a circuit is equal to the current (I) multiplied by the total resistance (R_total). In this case, the total resistance includes both the external resistance and the internal resistance of the cell.
\(
V = I \cdot R_{total}
\)
Where:
\(
R_{total} = R + r
\)
Here, r is the internal resistance of the cell.
3. Set up the equation:
We can express the total voltage as:
\(
E = I \cdot (R + r)
\)
Substituting the known values:
\(
2.1 = 0.2 \cdot (10 + r)
\)
4. Solve for r:
First, divide both sides by 0.2:
\(
\frac{2.1}{0.2} = 10 + r
\)
This simplifies to:
\(
10.5 = 10 + r
\)
Now, isolate r:
\(
r = 10.5 - 10
\)
\(
r = 0.5 \, \Omega
\)
5. Conclusion:
The internal resistance of the cell is 0.5Ω.
- EMF of the cell (E) = 2.1V
- Current (I) = 0.2A
- External resistance (R) = 10Ω
According to Ohm's Law, the total voltage (V) in a circuit is equal to the current (I) multiplied by the total resistance (R_total). In this case, the total resistance includes both the external resistance and the internal resistance of the cell.
V = I \cdot R_{total}
\)
\(
R_{total} = R + r
\)
We can express the total voltage as:
\(
E = I \cdot (R + r)
\)
Substituting the known values:
\(
2.1 = 0.2 \cdot (10 + r)
\)
First, divide both sides by 0.2:
\(
\frac{2.1}{0.2} = 10 + r
\)
This simplifies to:
\(
10.5 = 10 + r
\)
\(
r = 10.5 - 10
\)
\(
r = 0.5 \, \Omega
\)
The internal resistance of the cell is 0.5Ω.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns4videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
The internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionCalculate the current flows through resistance 2Ω.
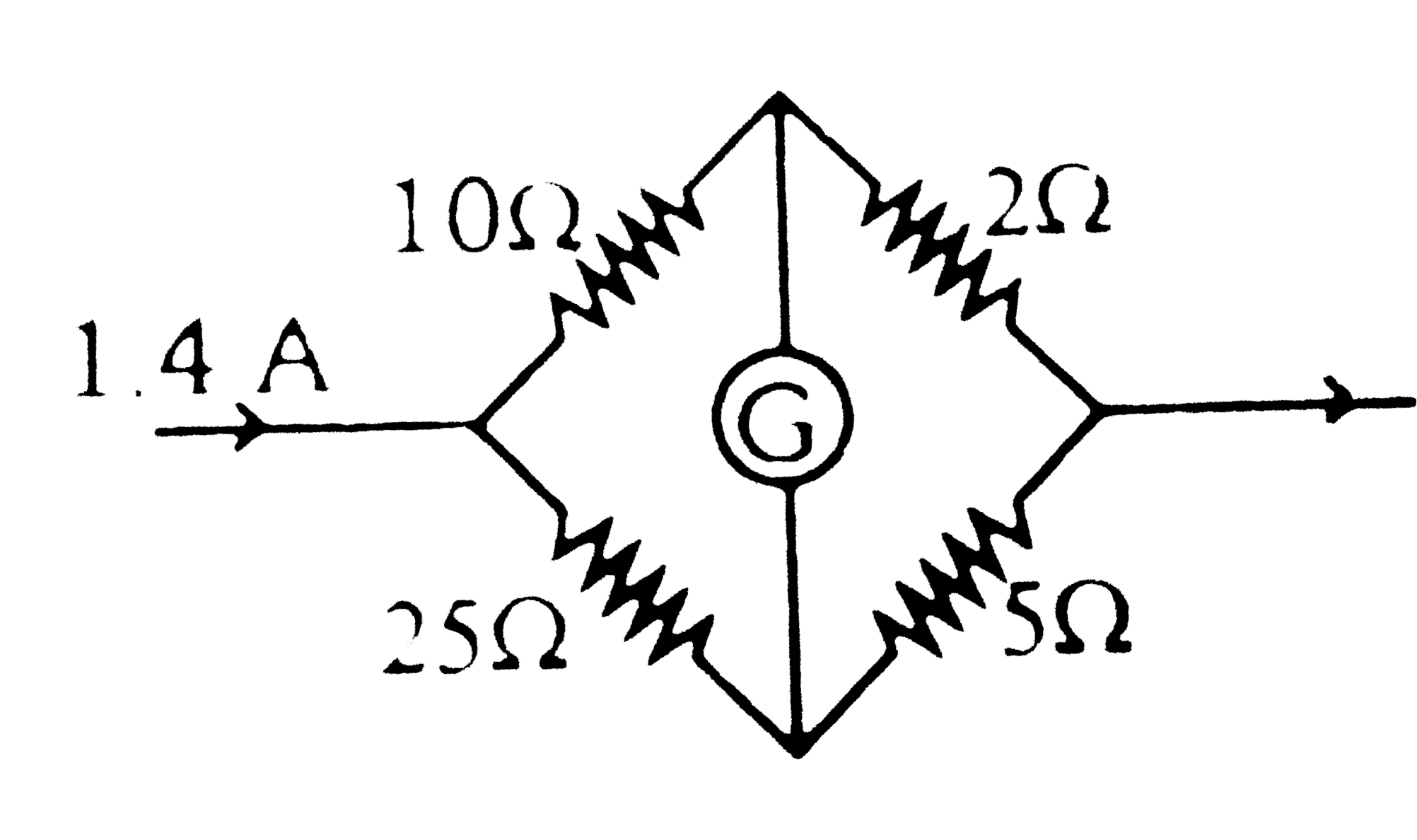 View Solution
View SolutionThe internal resistance of primary cell is 4Ω it genrater a current of 0.2A and connected to a external resistance 0f '21Omega' in which resistance connected is providing the the heat per second is
View SolutionFind the minimum number of cell required to produce an electron current of 1.5A through a resistance of 30Ω .Given that the emf internal resistance of each cell are 1.5V and 1.0Ω respectively
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionA 6 V cell with 0.5Ω internal resistance , a 10 v cell with 1Ω internal resistance and a 12Ω external resistance are connected in parallel . The current (in amper) through the 10 V cell is
View SolutionIn a meter bridge circuit, the two resistances in the gap are 5Ω and 10Ω. The wire resistance is 4Ω. The emf of the cell connected at the ends of the wire is 5V and its internal resistance is 1Ω. What current will flow through the galvenometer of resistance 30Ω if the contact is made at the midpoint of wire ?
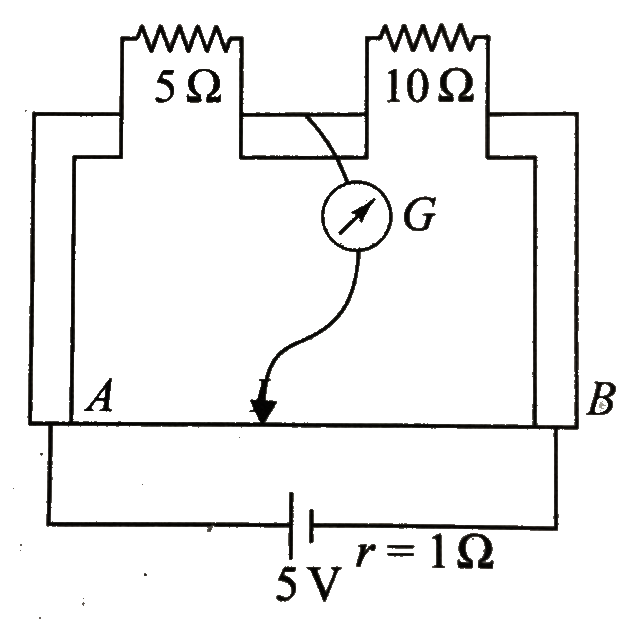 View Solution
View SolutionIn a mixed grouping of identical cells, five rows are connected in parallel and each row contains 10 cells. This combination sends a current I through an external resistance of 20Ω. if the emf and internal resistance of each cell is 1.5 V and 1Ω, respectively then find the value of I.
View SolutionA cell of e.m.f. ε and internal resistance r sends a current of 1.0 A when it is connected to an external resistance of 1.9 Ω. But it sends a current of 0.5 A when it is connected to an resistance of 3.9Ω calculate the values of ε and r .
View SolutionIn the circuit shown , the internal resistance of the cell is negligible . The steady stale current in the 2Ω resistor is
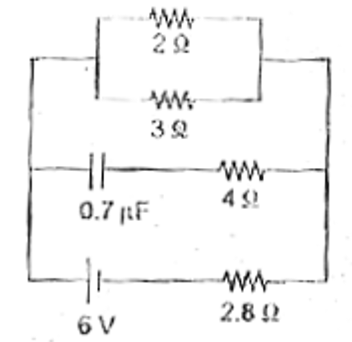 View Solution
View Solution

