When a wire of uniform cross-section a, length I and resistance R is bent into a complete circle, resistance between two of diametrically opposite points will be
R4
R8
4R
R2
The correct Answer is:A
To solve the problem of finding the resistance between two diametrically opposite points when a wire of uniform cross-section a, length L, and resistance R is bent into a complete circle, we can follow these steps:
Step 1: Understand the Configuration
When the wire is bent into a complete circle, it can be visualized as two semicircles. Each semicircle will have half the length of the original wire.
Step 2: Calculate the Length of Each Semicircle
The total length of the wire is L. When bent into a circle, the length of each semicircle is:
Lsemicircle=L2
Step 3: Determine the Resistance of Each Semicircle
The resistance R of the wire is given by:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area. Since the wire is now in two semicircles, the resistance of each semicircle can be calculated as:
Rsemicircle=R2
Step 4: Analyze the Resistance Between Two Opposite Points
The resistance between two diametrically opposite points involves the two semicircles. The resistances of the two semicircles are in parallel. The formula for the equivalent resistance RP of two resistances R1 and R2 in parallel is:
1RP=1R1+1R2
In this case, both R1 and R2 are equal to R2:
1RP=1R2+1R2=2R/2=4R
Step 5: Solve for the Equivalent Resistance
Now, we can find RP:
RP=R4
Conclusion
The resistance between two diametrically opposite points when the wire is bent into a complete circle is:
R4
---
When the wire is bent into a complete circle, it can be visualized as two semicircles. Each semicircle will have half the length of the original wire.
The total length of the wire is L. When bent into a circle, the length of each semicircle is:
Lsemicircle=L2
The resistance R of the wire is given by:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area. Since the wire is now in two semicircles, the resistance of each semicircle can be calculated as:
Rsemicircle=R2
The resistance between two diametrically opposite points involves the two semicircles. The resistances of the two semicircles are in parallel. The formula for the equivalent resistance RP of two resistances R1 and R2 in parallel is:
1RP=1R1+1R2
In this case, both R1 and R2 are equal to R2:
1RP=1R2+1R2=2R/2=4R
Now, we can find RP:
RP=R4
The resistance between two diametrically opposite points when the wire is bent into a complete circle is:
R4
Similar Questions
A wire of resistance 10(Ω)is bent to form a complete circle.Find its resistance between two diametrically opposite points.
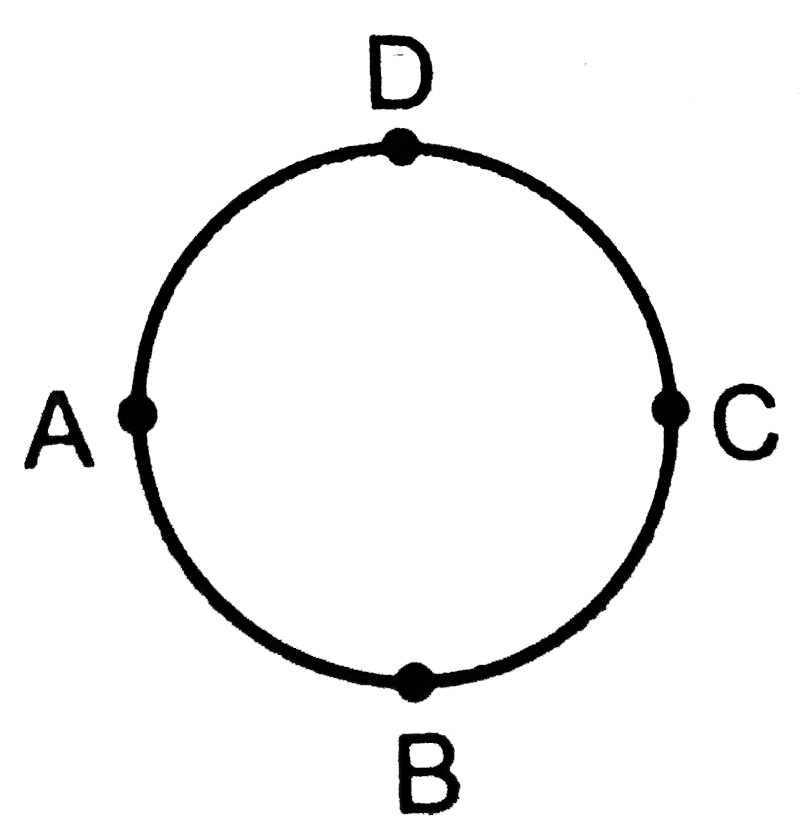
View SolutionA wire of resistance 20Ω is bent to form a complete circle. The resistance between two diametrically opposite points A and B as shown in the figure, is
View Solution
Knowledge Check
A wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is
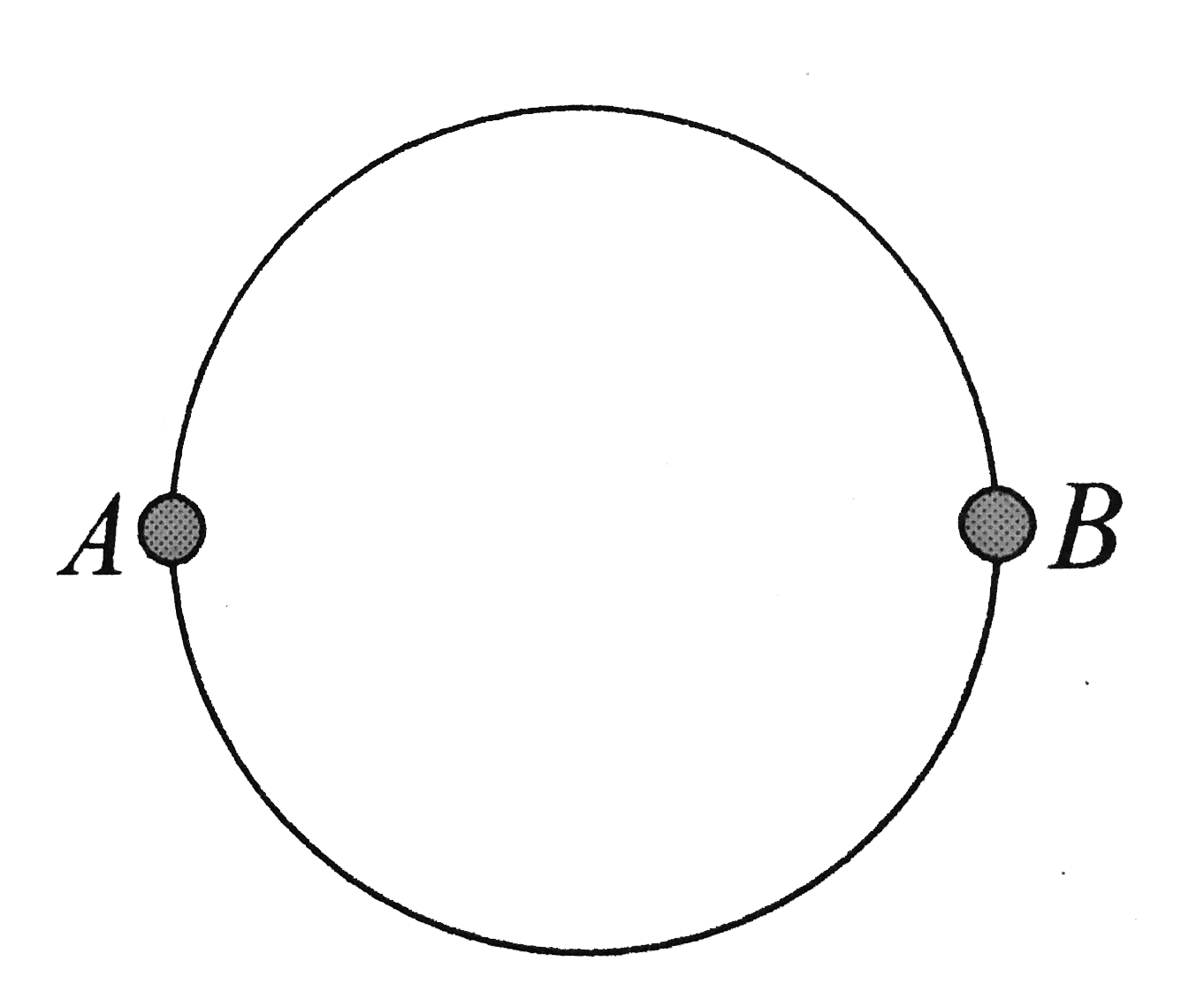 A3ΩB6πΩC6ΩD0.6πΩ
A3ΩB6πΩC6ΩD0.6πΩ
A metallic wire having a resistance of 20Ω is bent in order to form a complete circle. Calculate the resistance between any two diametrically opposite points on the circle.
View SolutionA uniform wire os resistance 12Ω is bent to form a circle. Effective resistance across two diametrically opposite points is
View SolutionA wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is

View SolutionA wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?
View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
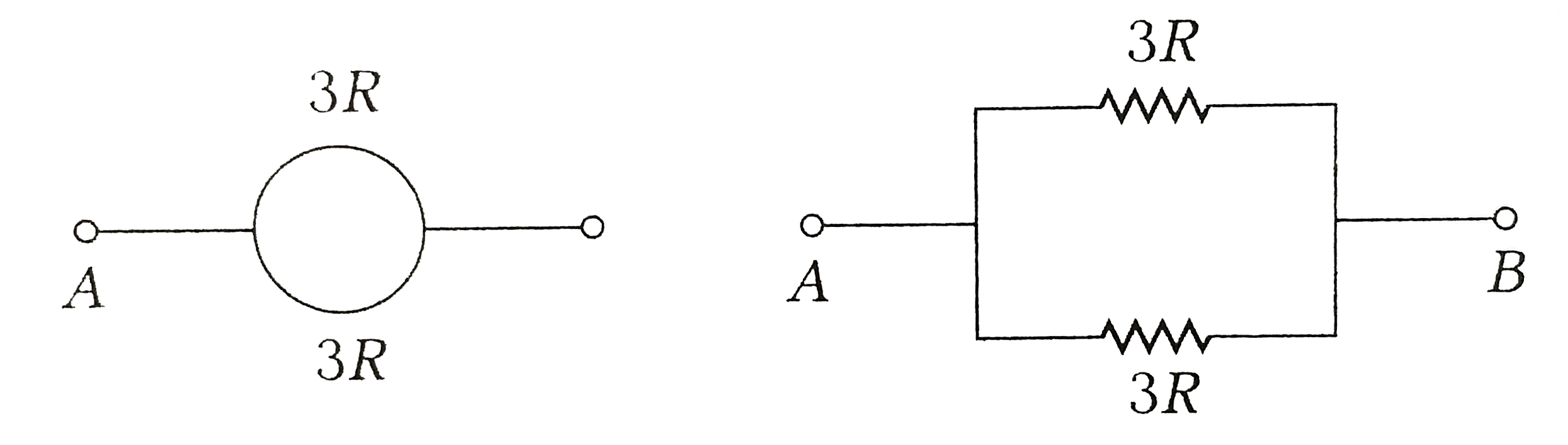
View SolutionA battery is connected across a resistance wire of uniform cross-section . If another resistance wire is connected in parallel, then the intensity of electric field in the first wire will
View SolutionA wire of resistance 4Ω is bent to form a circle. The resistance point A and B will be
_PHY_E05_303_Q01.png)
View Solution

