A battery is connected across a resistance wire of uniform cross-section . If another resistance wire is connected in parallel, then the intensity of electric field in the first wire will
be halved
be doubled
become zero
remain unchanged
The correct Answer is:D
To solve the problem, we need to analyze the situation when a second resistance wire is connected in parallel to the first wire. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Circuit Configuration
We have a battery connected across a resistance wire (let's call it R1) of uniform cross-section. When we connect another resistance wire (R2) in parallel to R1, we need to determine how this affects the electric field in the first wire (R1).
Hint: Visualize the circuit with the battery and the two resistors in parallel. This will help you understand the voltage distribution.
Step 2: Analyze the Electric Field
The intensity of the electric field (E) in a conductor can be expressed as:
E=−dVdx
where V is the potential difference across the wire and x is the length of the wire.
Hint: Remember that the electric field is related to the potential difference and the length of the conductor.
Step 3: Consider the Voltage Across the Wires
In a parallel circuit, the voltage across each component is the same. Therefore, when the second wire (R2) is connected in parallel with the first wire (R1), the voltage across R1 remains the same as the voltage supplied by the battery.
Hint: Think about how connecting components in parallel affects voltage.
Step 4: Evaluate the Length of the Wire
The length of the first wire (R1) does not change when R2 is added in parallel. Thus, the distance x in the equation for electric field remains constant.
Hint: The physical dimensions of R1 are unchanged by the addition of R2.
Step 5: Conclude the Effect on Electric Field
Since both the voltage (V) across R1 and the length (x) of R1 remain unchanged, the electric field E in the first wire will also remain unchanged.
Hint: Consider how changes in voltage or length would affect the electric field.
Final Answer
The intensity of the electric field in the first wire (R1) will remain unchanged when another resistance wire (R2) is connected in parallel.
Summary
- The electric field in the first wire remains constant because the voltage across it does not change and its length remains the same.
Answer: The intensity of electric field in the first wire will remain unchanged.
We have a battery connected across a resistance wire (let's call it R1) of uniform cross-section. When we connect another resistance wire (R2) in parallel to R1, we need to determine how this affects the electric field in the first wire (R1).
The intensity of the electric field (E) in a conductor can be expressed as:
E=−dVdx
where V is the potential difference across the wire and x is the length of the wire.
In a parallel circuit, the voltage across each component is the same. Therefore, when the second wire (R2) is connected in parallel with the first wire (R1), the voltage across R1 remains the same as the voltage supplied by the battery.
The length of the first wire (R1) does not change when R2 is added in parallel. Thus, the distance x in the equation for electric field remains constant.
Since both the voltage (V) across R1 and the length (x) of R1 remain unchanged, the electric field E in the first wire will also remain unchanged.
The intensity of the electric field in the first wire (R1) will remain unchanged when another resistance wire (R2) is connected in parallel.
- The electric field in the first wire remains constant because the voltage across it does not change and its length remains the same.
Similar Questions
When a wire of uniform cross-section a, length I and resistance R is bent into a complete circle, resistance between two of diametrically opposite points will be
View SolutionPower generated across a uniform wire connected across a supply is H. If the wire is cut into n equal parts and all the parts are connected in parallel across the same supply, the total power generated in the wire is
View SolutionA wire of resistance R is divided in 10 equal parts. These parts are connected in parallel, the equivalent resistance of such connection will be
View SolutionThe wire of same dimension but resistivities(p1) and (p2)are connected in parallel. The equivalent resistivity of the combination is
View SolutionConsider a resistor of uniform cross-sectional area connected to a battery of internal resistance zero. If the length of the resistor is doubled by stretching it, then
View SolutionAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
View SolutionAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
View SolutionIn fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
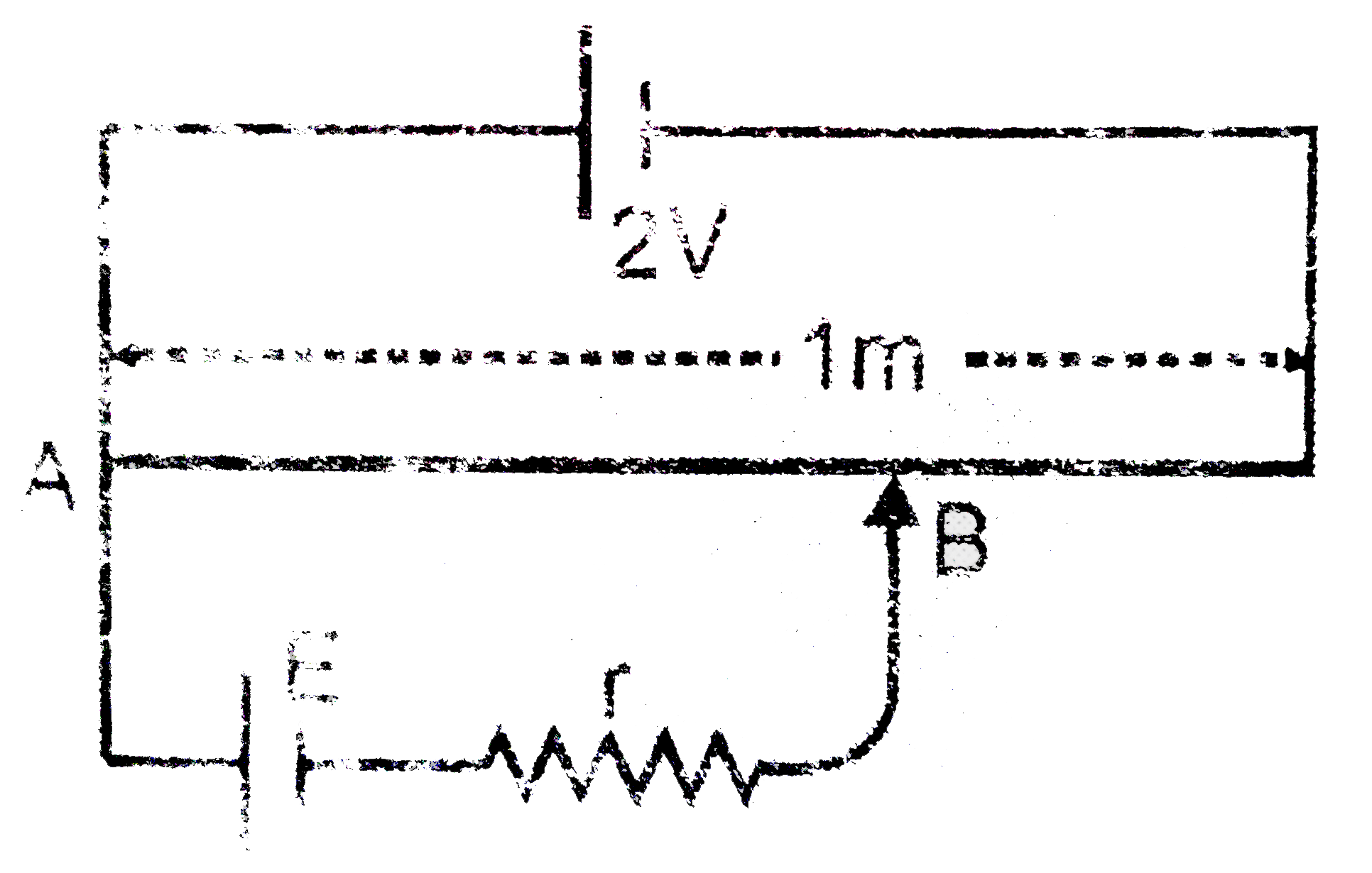
View SolutionA wire of resistance R is cut into ‘ n ’ equal parts. These parts are then connected in parallel. The equivalent resistance of the combination will be
View SolutionA battery is connected to a uniform resistance wire AB and B is earthed. Which one of the graphs below shows how the current density J varies along AB

View Solution
