A metallic wire having a resistance of is bent in order to form a complete circle. Calculate the resistance between any two diametrically opposite points on the circle.
To solve the problem of finding the resistance between two diametrically opposite points on a circular wire with a total resistance of 20 ohms, we can follow these steps:
1. Understand the Configuration:
- We have a metallic wire with a total resistance of 20 ohms that is bent into the shape of a circle.
- We need to find the resistance between two points (A and B) that are diametrically opposite to each other on the circle.
2. Identify the Arcs:
- When the wire is bent into a circle, it can be divided into two arcs: Arc A to O' and Arc O' to B, where O' is the midpoint of the diameter AB.
- Each arc will have equal resistance due to symmetry.
3. Calculate Resistance of Each Arc:
- Since the total resistance of the wire is 20 ohms and it is evenly distributed, the resistance of each arc (from A to O' and from O' to B) will be half of the total resistance.
- Therefore, the resistance of each arc (R1 and R2) is:
R1=R2=20Ω2=10Ω
4. Combine the Resistances:
- The two arcs (R1 and R2) are in parallel when measuring the resistance between points A and B.
- The formula for the equivalent resistance (R_eq) for two resistors in parallel is given by:
1Req=1R1+1R2
- Substituting R1 and R2:
1Req=110+110=210=15
5. Calculate the Equivalent Resistance:
- Taking the reciprocal gives us the equivalent resistance:
Req=5Ω
6. Conclusion:
- The resistance between any two diametrically opposite points on the circle is 5 ohms.
Final Answer:
The resistance between any two diametrically opposite points on the circle is 5 ohms.
- We have a metallic wire with a total resistance of 20 ohms that is bent into the shape of a circle.
- We need to find the resistance between two points (A and B) that are diametrically opposite to each other on the circle.
- When the wire is bent into a circle, it can be divided into two arcs: Arc A to O' and Arc O' to B, where O' is the midpoint of the diameter AB.
- Each arc will have equal resistance due to symmetry.
- Since the total resistance of the wire is 20 ohms and it is evenly distributed, the resistance of each arc (from A to O' and from O' to B) will be half of the total resistance.
- Therefore, the resistance of each arc (R1 and R2) is:
R1=R2=20Ω2=10Ω
- The two arcs (R1 and R2) are in parallel when measuring the resistance between points A and B.
- The formula for the equivalent resistance (R_eq) for two resistors in parallel is given by:
1Req=1R1+1R2
- Substituting R1 and R2:
1Req=110+110=210=15
- Taking the reciprocal gives us the equivalent resistance:
Req=5Ω
- The resistance between any two diametrically opposite points on the circle is 5 ohms.
The resistance between any two diametrically opposite points on the circle is 5 ohms.
Similar Questions
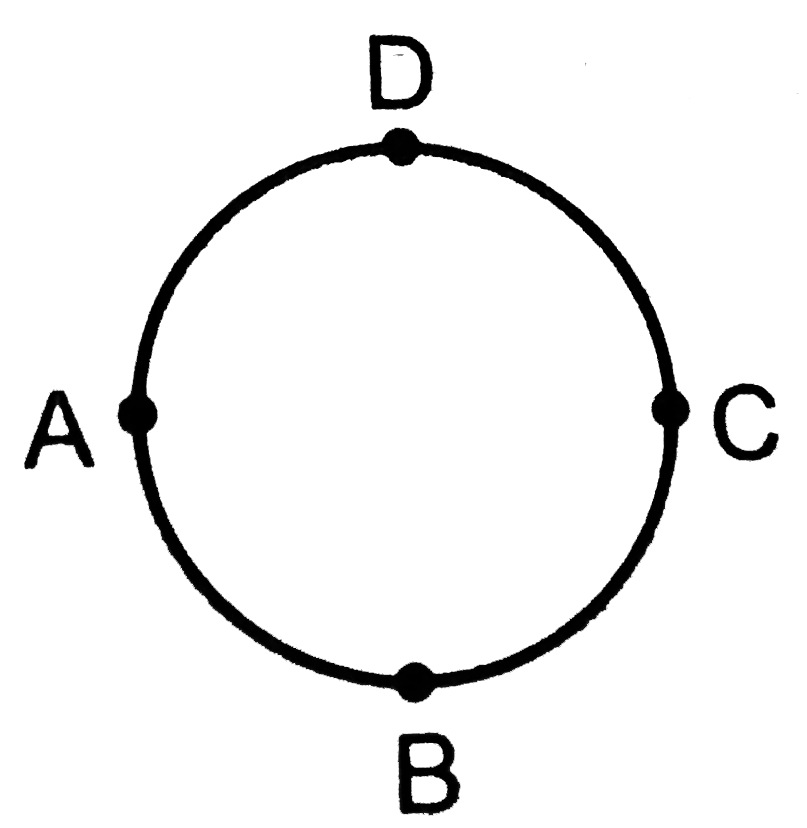
A wire of resistance 20Ω is bent to form a complete circle. The resistance between two diametrically opposite points A and B as shown in the figure, is
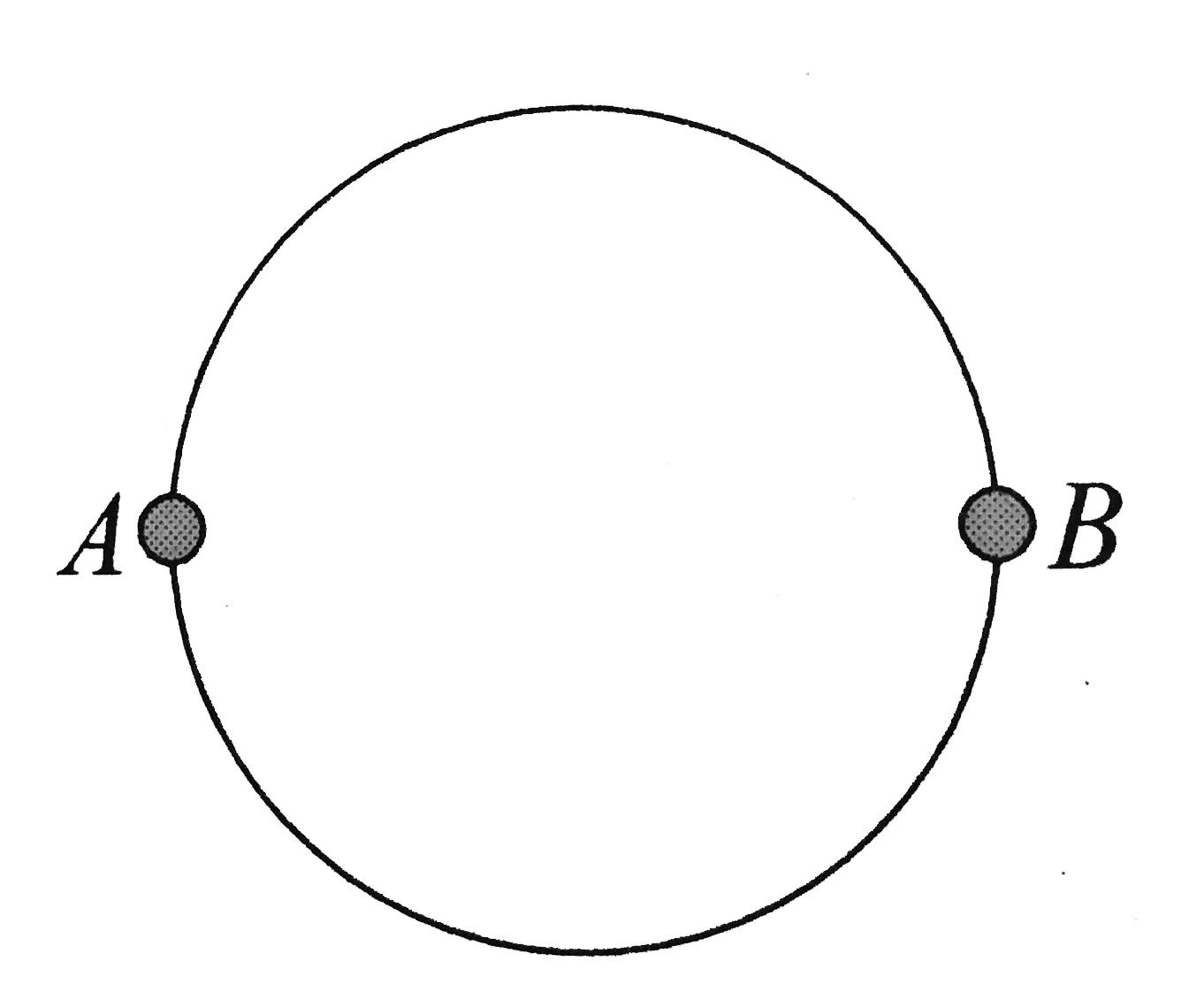
View SolutionA wire of resistance 10(Ω)is bent to form a complete circle.Find its resistance between two diametrically opposite points.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is
 A3ΩB6πΩC6ΩD0.6πΩ
A3ΩB6πΩC6ΩD0.6πΩ
A wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is
 View Solution
View SolutionWhen a wire of uniform cross-section a, length I and resistance R is bent into a complete circle, resistance between two of diametrically opposite points will be
View SolutionA wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
View SolutionA uniform wire of resistance 9Ω is joined end-to-end to from a circle. Then, the resistance of the circular wire between any two diametrically points is
View SolutionA uniform metallic wire has a resistance of 18 Ω and is bent into an equiolateral triangle. Then, the resistance between any two vertices of the triangle is :
View SolutionA uniform wire os resistance 12Ω is bent to form a circle. Effective resistance across two diametrically opposite points is
View SolutionA wire has resistance of 24Ω is bent in the following shape. The effective resistance between A and B is
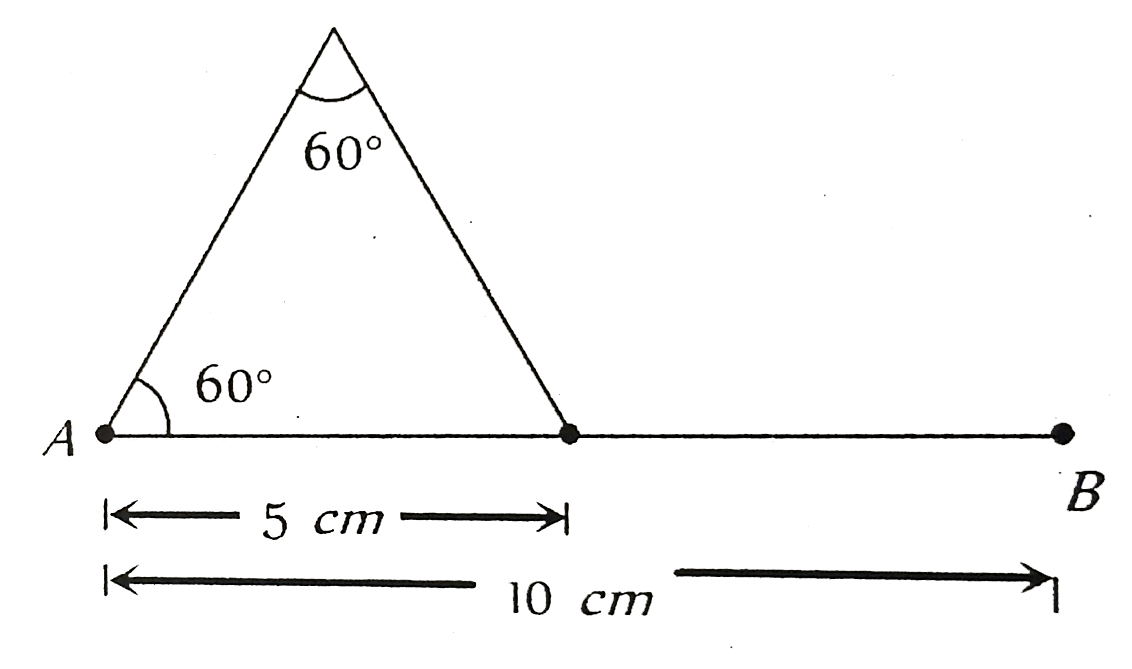 View Solution
View Solution


