You are given several identical resistors each of value 10Ω and each capable of carrying a maximum current of 1 A. It is required to make a suitable combination of these to resistances to produce a resistance of 5Ω which can carry a current of 4 A. The minimum number of resistors required for this job is
4
10
8
20
The correct Answer is:C
To solve the problem of combining several identical resistors of 10Ω each, capable of carrying a maximum current of 1A, to produce a resistance of 5Ω that can carry a total current of 4A, we can follow these steps:
Step 1: Understand the requirements
We need to create a total resistance of 5Ω and ensure that the combination can handle a total current of 4A. Since each resistor can only handle 1A, we will need to arrange them in such a way that we can achieve this current capacity.
Step 2: Determine the configuration
To achieve a total current of 4A, we can use parallel branches. Each branch can carry 1A, so we will need 4 branches to carry a total of 4A.
Step 3: Calculate the equivalent resistance of each branch
Let Rs be the resistance of each branch. Since we need 4 branches in parallel, the total resistance Rnet can be expressed as:
1Rnet=1Rs+1Rs+1Rs+1Rs=4Rs
Thus,
Rnet=Rs4
Step 4: Set up the equation for total resistance
We want Rnet=5Ω. Therefore, we can set up the equation:
5=Rs4
From this, we can solve for Rs:
Rs=5×4=20Ω
Step 5: Determine the number of resistors in each branch
Since each resistor has a resistance of 10Ω, we need to find out how many resistors are required to make Rs=20Ω. If we connect two 10Ω resistors in series, we get:
Rs=10+10=20Ω
Thus, we need 2 resistors in each branch.
Step 6: Calculate the total number of resistors
Since we have 4 branches and each branch requires 2 resistors, the total number of resistors required is:
Total resistors=4×2=8
Conclusion
The minimum number of resistors required to achieve the desired resistance and current capacity is 8.
We need to create a total resistance of 5Ω and ensure that the combination can handle a total current of 4A. Since each resistor can only handle 1A, we will need to arrange them in such a way that we can achieve this current capacity.
To achieve a total current of 4A, we can use parallel branches. Each branch can carry 1A, so we will need 4 branches to carry a total of 4A.
Let Rs be the resistance of each branch. Since we need 4 branches in parallel, the total resistance Rnet can be expressed as:
1Rnet=1Rs+1Rs+1Rs+1Rs=4Rs
Thus,
Rnet=Rs4
We want Rnet=5Ω. Therefore, we can set up the equation:
5=Rs4
From this, we can solve for Rs:
Rs=5×4=20Ω
Since each resistor has a resistance of 10Ω, we need to find out how many resistors are required to make Rs=20Ω. If we connect two 10Ω resistors in series, we get:
Rs=10+10=20Ω
Thus, we need 2 resistors in each branch.
Since we have 4 branches and each branch requires 2 resistors, the total number of resistors required is:
Total resistors=4×2=8
The minimum number of resistors required to achieve the desired resistance and current capacity is 8.
Similar Questions
You are given several identical resisters each of value 5Ω and each capable of carrying a maximum current of 2A. It is required to make a suitable combination of these resistance to produce a resistance of 2.5Ω which can carry current of 4A. The minimum number of resistances required for this job is
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View SolutionIn the given circuit diagram if each resistance is of 10Ω, then the current in arm AD will be
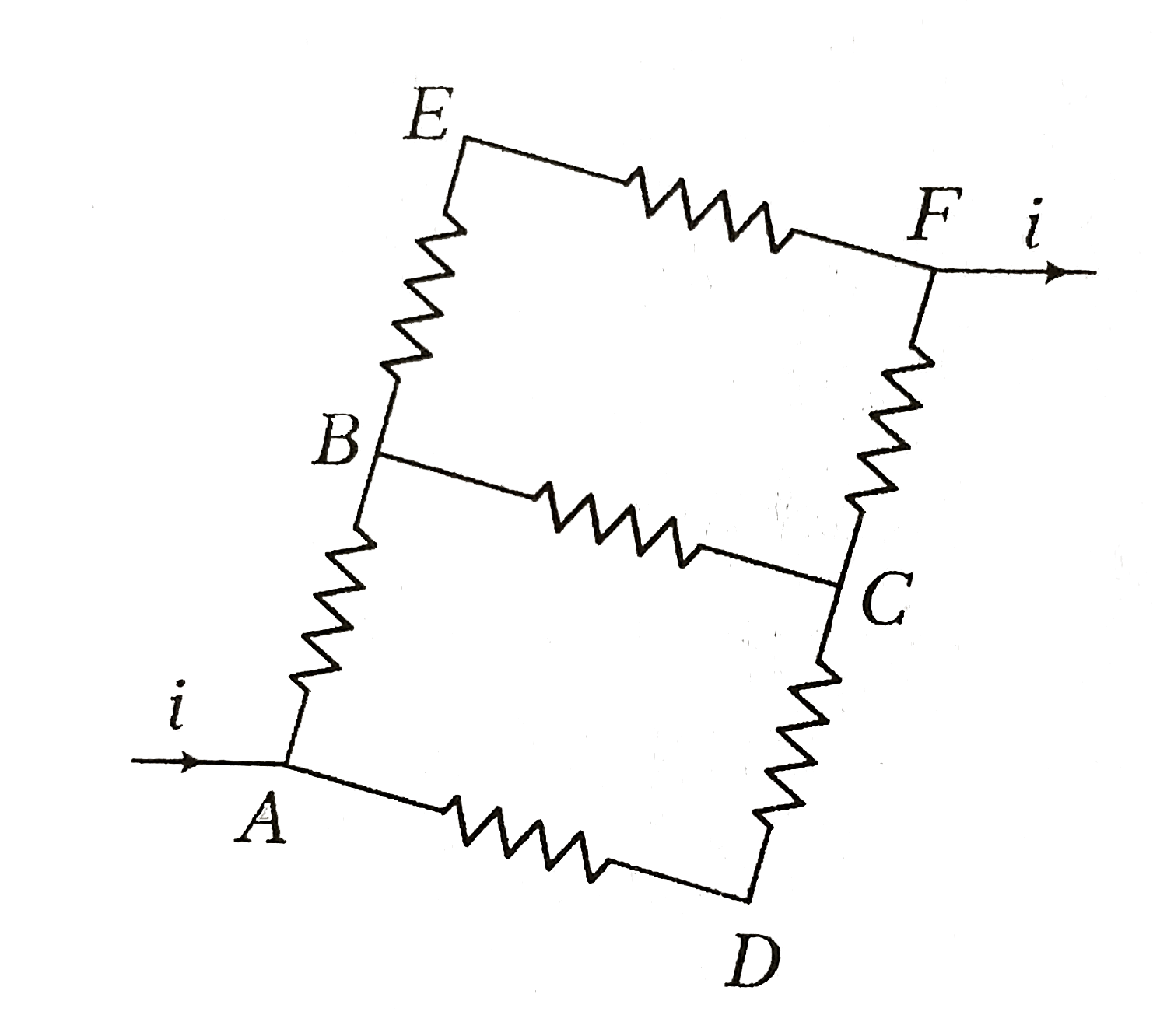
View SolutionCalculate the potential difference required across a conductor of resistance 5 Ω to pass a current of 1.5 A through it.
View SolutionFive identical resistors each of resistance 1Ω are initially arranged as shown in the figure by clear lines. If two resistances are added as shown by the dashed lines then change in resistance in final and initial arrangement is

View SolutionThree identical cells each of emf 2 V and internal resistance 1Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6Ω Find the current delivered by the battery.
View SolutionA galvanometer of resistance 40Ω can measure a current of 10mA To convert it into a voltmeter of range 8V the required resistance is ___________ Ω.
View SolutionCalculate the quantity of heat produced in a 20Ω resistor carrying 2.5 A current in 5 minutes.
View SolutionEach resistor shown in the figure has a resistance of 10Ω and the battery has the emf 6 V. What will be the current supplied by the battery ?
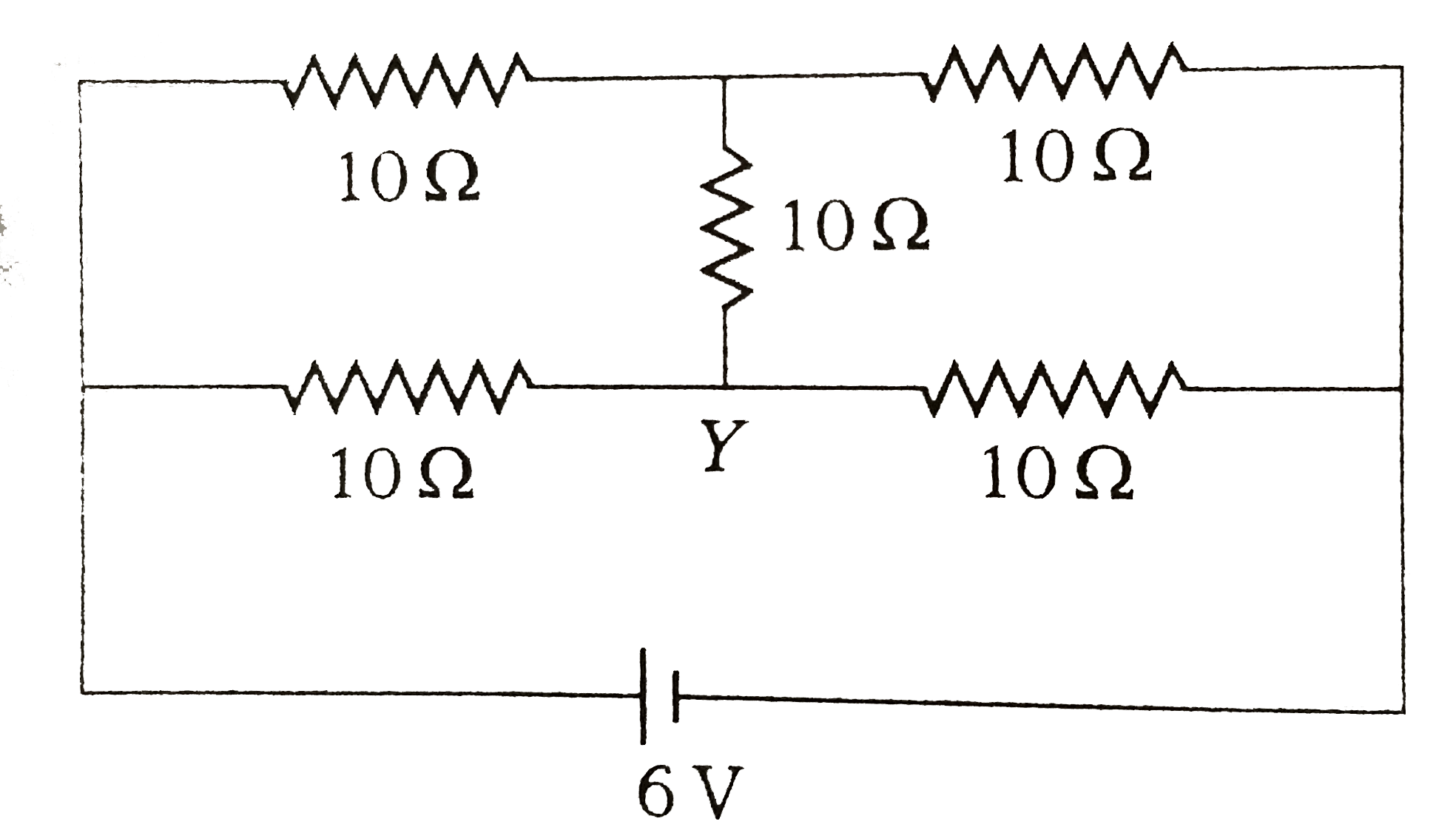
View SolutionTo get maximum current through a resistance of 2.5Ω, one can use m rows of cells, each row having n cells. The internal resistance of each cell is 0.5Ω what are the values of n and m, if the total number of cells is 45.
View Solution
