To get maximum current through a resistance of 2.5Ω, one can use m rows of cells, each row having n cells. The internal resistance of each cell is 0.5Ω what are the values of n and m, if the total number of cells is 45.
3,15
5,6
9,5
15,3
The correct Answer is:D
To solve the problem, we need to find the values of n (the number of cells in each row) and m (the number of rows) such that the total number of cells is 45, and we achieve maximum current through a resistance of 2.5Ω with each cell having an internal resistance of 0.5Ω.
1. Understanding the Configuration:
- Each row has n cells.
- The total number of cells is given as 45, so we can write the equation:
n×m=45
2. Calculating EMF and Internal Resistance:
- The EMF of each row is nE (where E is the EMF of a single cell).
- The internal resistance of each row is 0.5n.
- If m rows are connected in parallel, the total internal resistance Rinternal becomes:
Rinternal=0.5nm
3. Total Resistance in the Circuit:
- The total resistance Rtotal in the circuit is the sum of the external resistance RL and the internal resistance:
Rtotal=RL+Rinternal=2.5+0.5nm
4. Current Expression:
- The current I through the circuit can be expressed as:
I=EtotalRtotal=nE2.5+0.5nm
5. Substituting for m:
- From the equation n×m=45, we can express m as:
m=45n
- Substitute m into the current equation:
I=nE2.5+0.5n45n=nE2.5+0.5n245=nE2.5+n290
6. Maximizing Current:
- To find the value of n that maximizes the current, we differentiate I with respect to n and set the derivative to zero:
dIdn=0
- After differentiating and simplifying, we arrive at:
2.5=n290
- Rearranging gives:
n2=2.5×90=225
- Taking the square root:
n=15
7. Finding m:
- Substitute n back into the equation for m:
m=45n=4515=3
Final Answer:
Thus, the values of n and m are:
n=15,m=3
- Each row has n cells.
- The total number of cells is given as 45, so we can write the equation:
n×m=45
- The EMF of each row is nE (where E is the EMF of a single cell).
- The internal resistance of each row is 0.5n.
- If m rows are connected in parallel, the total internal resistance Rinternal becomes:
Rinternal=0.5nm
- The total resistance Rtotal in the circuit is the sum of the external resistance RL and the internal resistance:
Rtotal=RL+Rinternal=2.5+0.5nm
- The current I through the circuit can be expressed as:
I=EtotalRtotal=nE2.5+0.5nm
- From the equation n×m=45, we can express m as:
m=45n
- Substitute m into the current equation:
I=nE2.5+0.5n45n=nE2.5+0.5n245=nE2.5+n290
- To find the value of n that maximizes the current, we differentiate I with respect to n and set the derivative to zero:
dIdn=0
- After differentiating and simplifying, we arrive at:
2.5=n290
- Rearranging gives:
n2=2.5×90=225
- Taking the square root:
n=15
- Substitute n back into the equation for m:
m=45n=4515=3
Thus, the values of n and m are:
n=15,m=3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct16videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension35videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective29videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
For the given circuit,
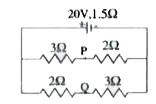
If internal resistance of cell is 1.5Ω, thenView SolutionTo get maximum current in a resistance of 3Ω, one can use n parallel rows of m cells each (connected in series). If the total no. of cells is 24 and the internal resistance is 0.5 ohm then
View SolutionTo get a maximum current in an external resistance of 8Ω one can use m rows of n cells (connected in series), connected in parallel. If the total number of cells is 64 each having an e.m.f. of 2V and interanl resistance of 2Ω , then calculate the number of cells in each row and number of rows.
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View Solution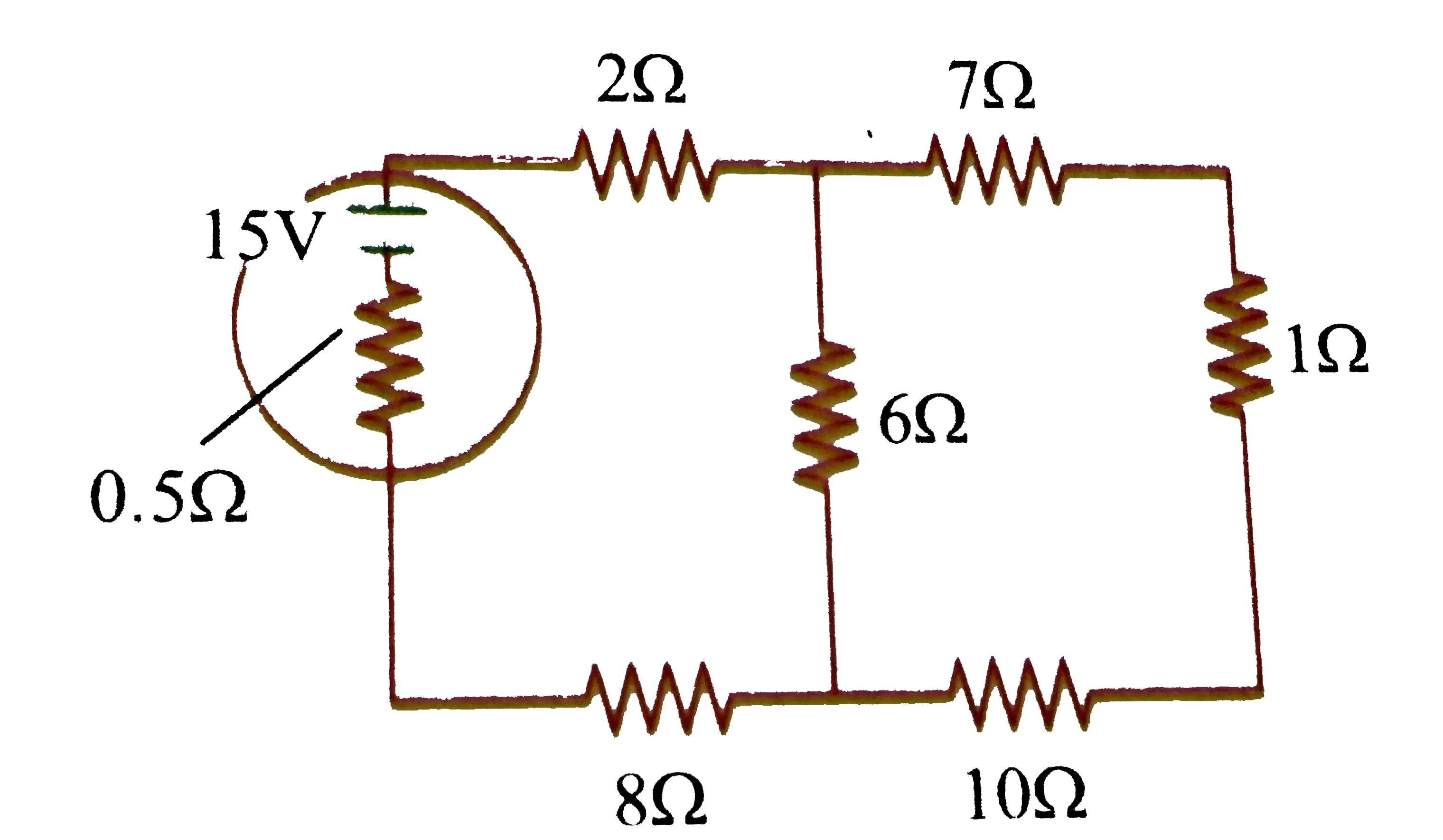
The emf of a cell E is 15 V as shown in the figure with an internal resistance of 0.5Ω. Then the value of the current drawn from the cell isView Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionThe internal resistances of two cells shown are 0.1Ω and 0.3Ω. If R=0.2Ω, its potential difference across the cell
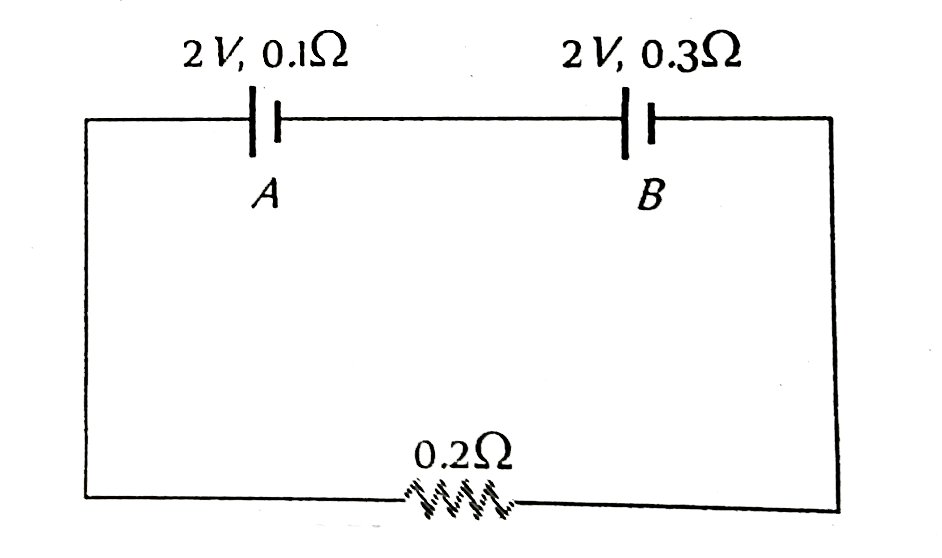 View Solution
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionA resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
View Solution

