You are given several identical resisters each of value and each capable of carrying a maximum current of 2A. It is required to make a suitable combination of these resistance to produce a resistance of which can carry current of 4A. The minimum number of resistances required for this job is
2
4
6
8
The correct Answer is:A
To solve the problem, we need to find the minimum number of 5Ω resistors required to create a total resistance of 2.5Ω that can carry a current of 4A.
1. Identify the Required Resistance and Current:
- We need a total resistance Req=2.5Ω.
- The total current Itotal=4A.
2. Understand the Configuration of Resistors:
- Each resistor has a resistance of R=5Ω.
- Each resistor can carry a maximum current of Imax=2A.
3. Determine the Required Configuration:
- Since 2.5Ω is less than 5Ω, we need to connect the resistors in parallel.
- The formula for the equivalent resistance Req of two identical resistors R in parallel is given by:
Req=Rn
where n is the number of resistors in parallel.
4. Calculate the Number of Resistors Needed for 2.5Ω:
- Setting Req=2.5Ω and R=5Ω:
2.5=5n
- Rearranging gives:
n=52.5=2
- Therefore, we need 2 resistors in parallel to achieve a resistance of 2.5Ω.
5. Check the Current Carrying Capacity:
- When two resistors are in parallel, the total current Itotal is the sum of the currents through each resistor:
Itotal=I1+I2
- Since each resistor can carry a maximum of 2A, the total current through the two resistors in parallel is:
Itotal=2A+2A=4A
- This matches the required current of 4A.
6. Conclusion:
- The minimum number of resistors required to achieve a resistance of 2.5Ω and carry a current of 4A is 2 resistors.
Final Answer:
The minimum number of resistors required is 2.
- We need a total resistance Req=2.5Ω.
- The total current Itotal=4A.
- Each resistor has a resistance of R=5Ω.
- Each resistor can carry a maximum current of Imax=2A.
- Since 2.5Ω is less than 5Ω, we need to connect the resistors in parallel.
- The formula for the equivalent resistance Req of two identical resistors R in parallel is given by:
Req=Rn
where n is the number of resistors in parallel.
- Setting Req=2.5Ω and R=5Ω:
2.5=5n
- Rearranging gives:
n=52.5=2
- Therefore, we need 2 resistors in parallel to achieve a resistance of 2.5Ω.
- When two resistors are in parallel, the total current Itotal is the sum of the currents through each resistor:
Itotal=I1+I2
- Since each resistor can carry a maximum of 2A, the total current through the two resistors in parallel is:
Itotal=2A+2A=4A
- This matches the required current of 4A.
- The minimum number of resistors required to achieve a resistance of 2.5Ω and carry a current of 4A is 2 resistors.
The minimum number of resistors required is 2.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - II LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - II LEVEL-II (ADVANCED) (Matrix matching Type Questions))
1 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - I LEVEL-II (ADVANCED) (Integer Type Questions))
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
You are given several identical resistors each of value 10Ω and each capable of carrying a maximum current of 1 A. It is required to make a suitable combination of these to resistances to produce a resistance of 5Ω which can carry a current of 4 A. The minimum number of resistors required for this job is
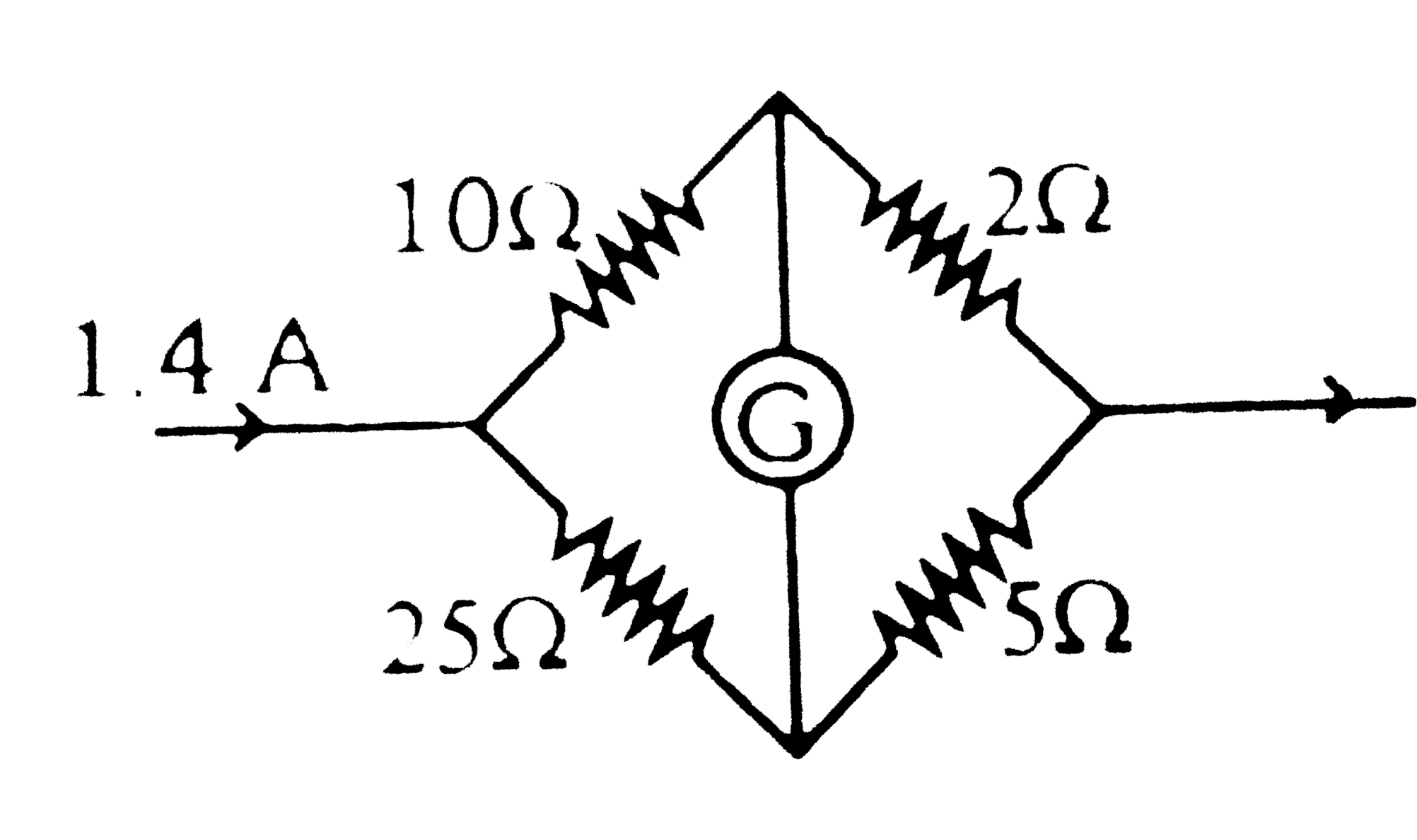
View SolutionCalculate the current flows through resistance 2Ω.
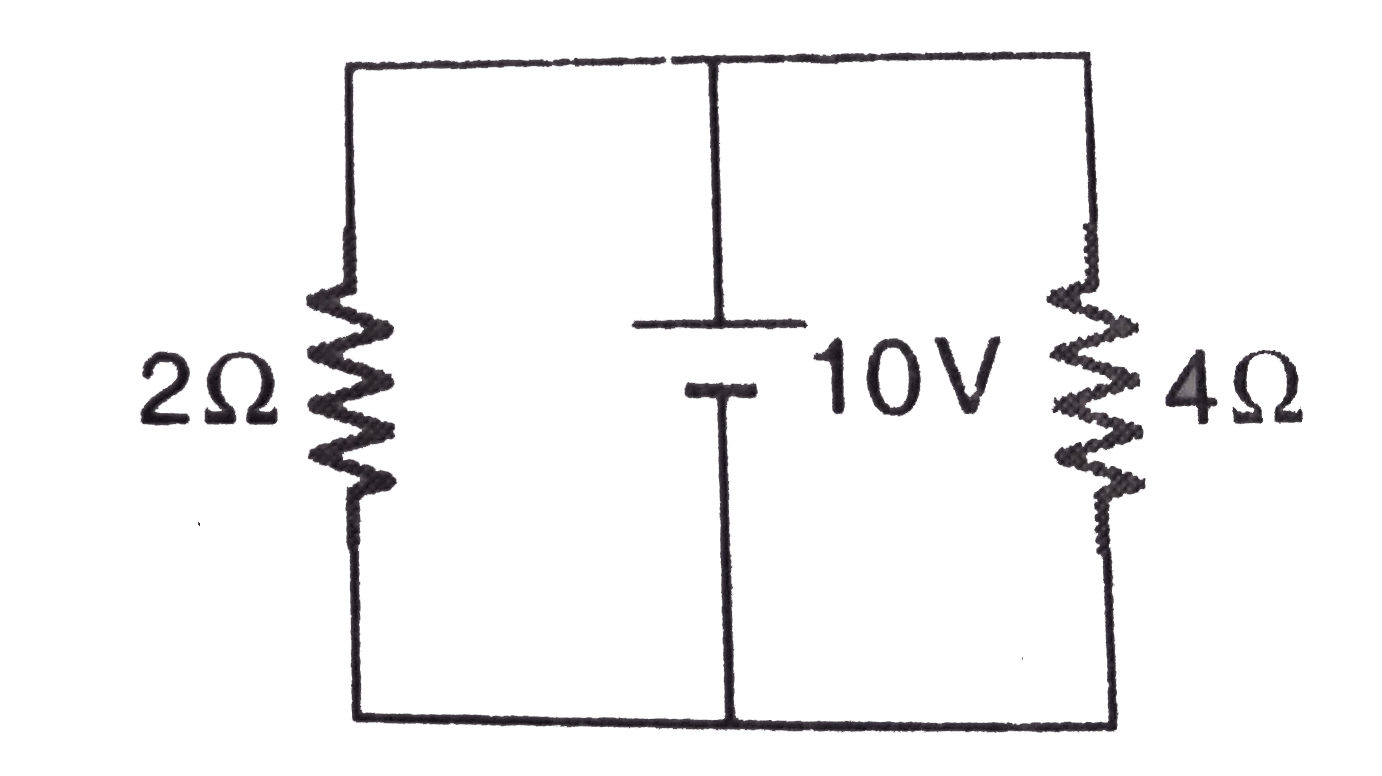
View SolutionFind the current through 2Ω and 4Ω resistance.
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionA direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
View SolutionA direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
View SolutionA direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
View SolutionCalculate the potential difference required across a conductor of resistance 5 Ω to pass a current of 1.5 A through it.
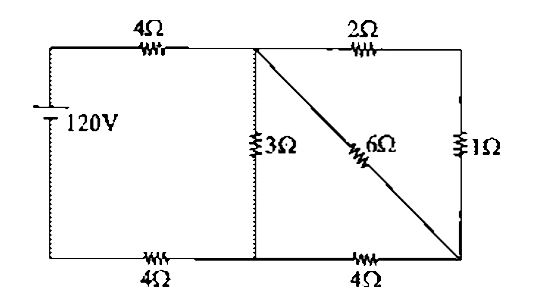
View SolutionFind the current in 2Ω resistance
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View Solution
