A battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
0.5Ω
1.0Ω
2.0Ω
0.25Ω
The correct Answer is:A
To find the value of the variable resistance R for which the power delivered in it is maximum, we can follow these steps:
Step 1: Understand the Circuit
We have a battery with an electromotive force (e.m.f) of 10V and an internal resistance r=0.5Ω. The battery is connected to a variable resistor R.
Step 2: Write the Expression for Power
The total resistance in the circuit is the sum of the internal resistance and the variable resistance:
Rtotal=R+r=R+0.5Ω
The power P delivered to the resistor R can be expressed as:
P=V2R2total⋅R=102(R+0.5)2⋅R
This simplifies to:
P=100R(R+0.5)2
Step 3: Differentiate Power with Respect to R
To find the maximum power, we need to differentiate P with respect to R and set the derivative equal to zero:
dPdR=(R+0.5)2⋅100−100R⋅2(R+0.5)(R+0.5)4
Setting the numerator equal to zero gives:
(R+0.5)2⋅100−200R(R+0.5)=0
Step 4: Solve the Equation
Expanding and simplifying the equation:
100(R+0.5)2=200R(R+0.5)
100(R2+R+0.25)=200R2+100R
100R2+100R+25=200R2+100R
0=100R2−25
100R2=25
R2=0.25
R=0.5Ω
Step 5: Conclusion
The value of R for which the power delivered in it is maximum is:
0.5Ω
---
We have a battery with an electromotive force (e.m.f) of 10V and an internal resistance r=0.5Ω. The battery is connected to a variable resistor R.
The total resistance in the circuit is the sum of the internal resistance and the variable resistance:
Rtotal=R+r=R+0.5Ω
The power P delivered to the resistor R can be expressed as:
P=V2R2total⋅R=102(R+0.5)2⋅R
This simplifies to:
P=100R(R+0.5)2
To find the maximum power, we need to differentiate P with respect to R and set the derivative equal to zero:
dPdR=(R+0.5)2⋅100−100R⋅2(R+0.5)(R+0.5)4
Setting the numerator equal to zero gives:
(R+0.5)2⋅100−200R(R+0.5)=0
Expanding and simplifying the equation:
100(R+0.5)2=200R(R+0.5)
100(R2+R+0.25)=200R2+100R
100R2+100R+25=200R2+100R
0=100R2−25
100R2=25
R2=0.25
R=0.5Ω
The value of R for which the power delivered in it is maximum is:
0.5Ω
Similar Questions
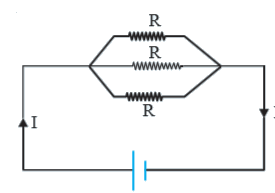
Three equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
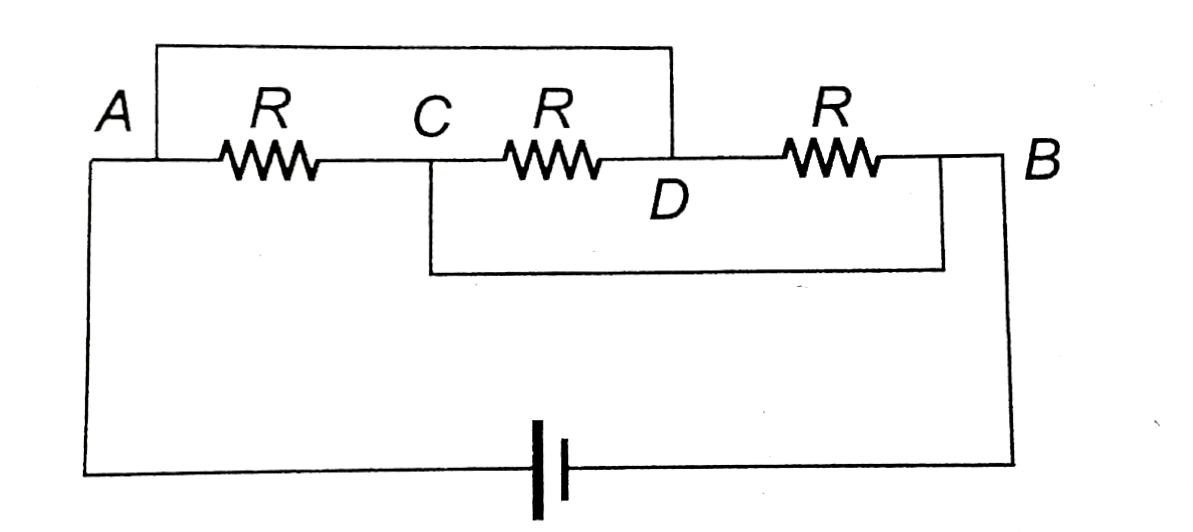
View SolutionA battery of ε and internal resistance r is used in a circuit with a variable external resistance R. Find the value of R for which the power consumed in R is maximum.
View Solution
Knowledge Check
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A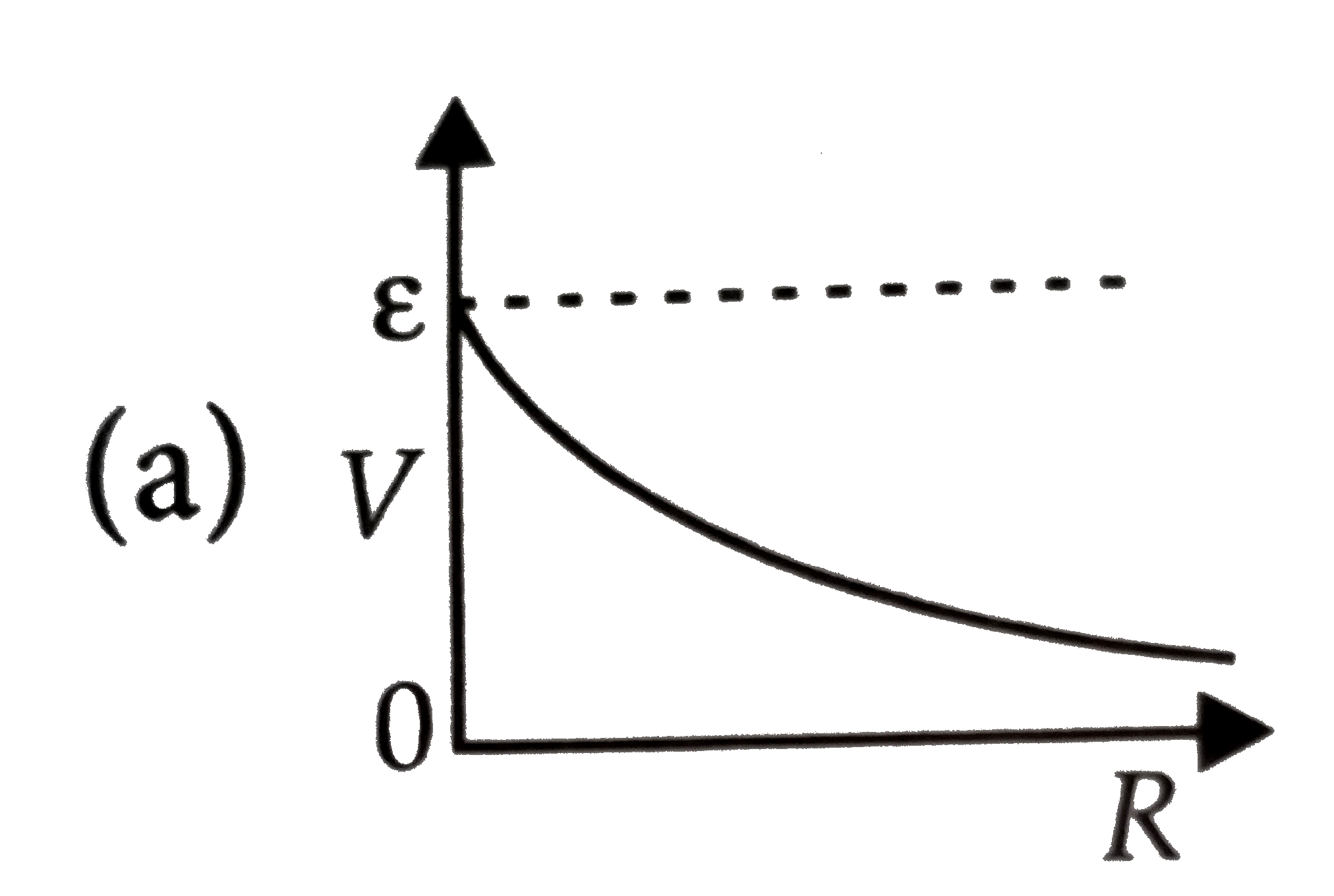 B
B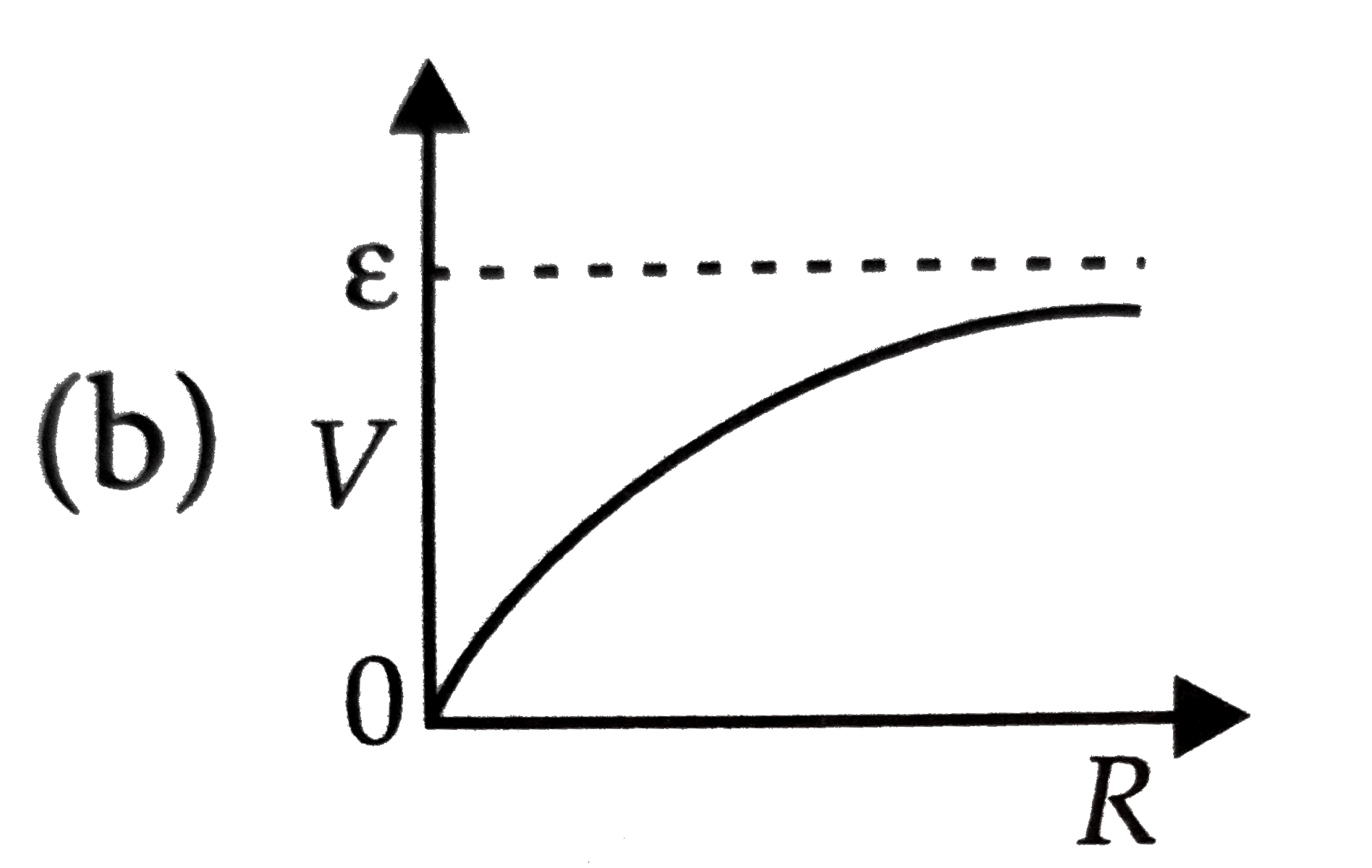 C
C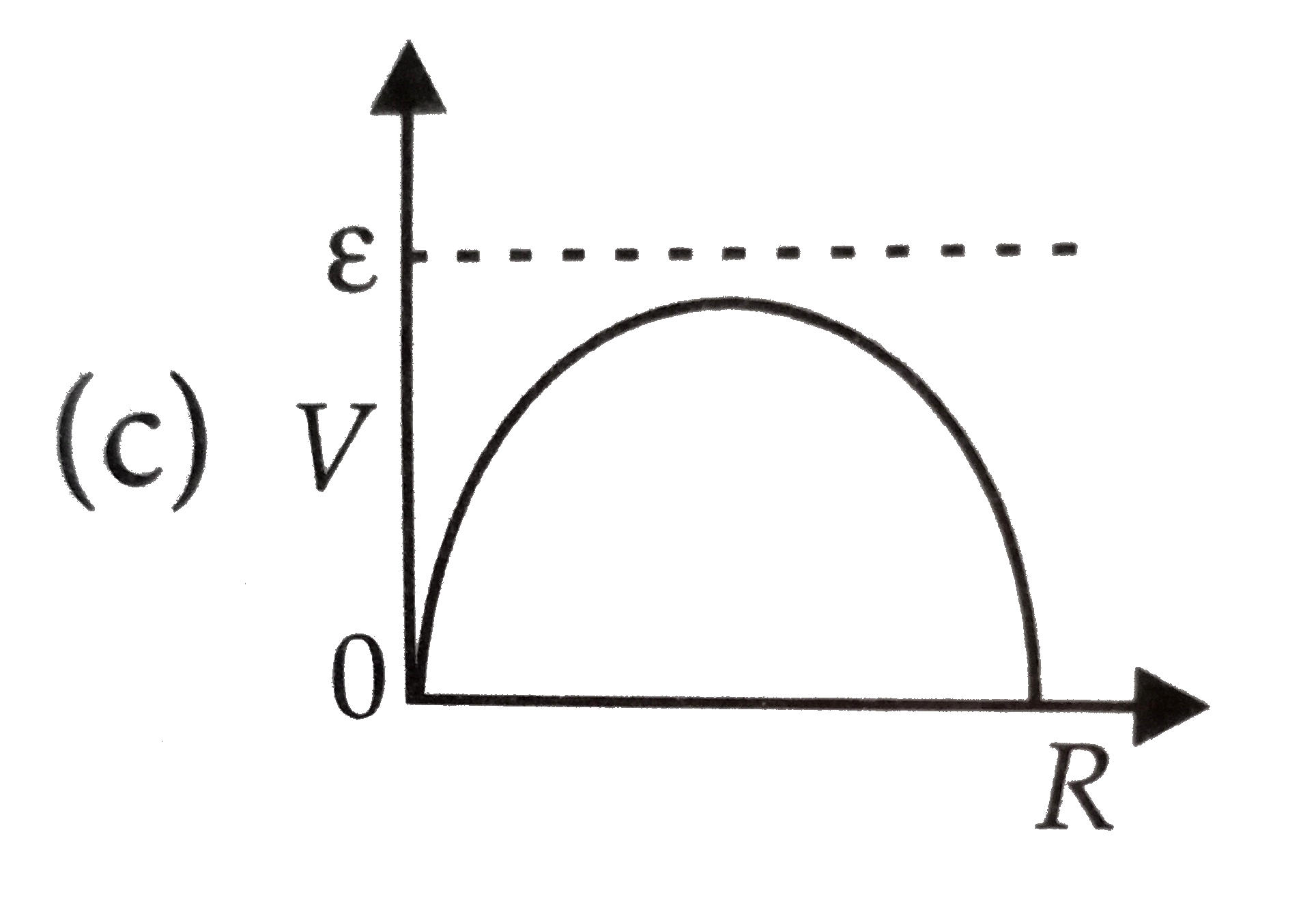 D
D
Three equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA battery of emf epsilon and internal resistance r is connected across a load resistance RL . The plot between output power and load resistance is shown in the figure. The value of emf epsilon and internal resistance r respectively will
_PHY_E05_112_Q01.png)
View Solution2A cell having an emf ε and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionA 24 V battery of internal resistance 4.0Ω is connected to a variable resistance. At what value of the current drawn from the battery is the rate of heat produced in the resistor maximum?
View Solution
