A square current carrying loop is suspended in a unifrom magnetic field acting in the plane of the loop. If the force on one arm of the loop is →F, the net force on the remaining three arms of the loop is
3F
−F
−3F
F
The correct Answer is:b
To solve the problem, let's analyze the situation step by step.
Step 1: Understand the Configuration
We have a square current-carrying loop suspended in a uniform magnetic field. The magnetic field is acting in the plane of the loop. Let's denote the arms of the loop as A, B, C, and D.
Hint: Visualize the square loop and the direction of the magnetic field.
Step 2: Identify the Force on One Arm
We are given that the force on one arm of the loop (let's say arm A) is →F. This force is due to the interaction of the magnetic field with the current flowing through that arm.
Hint: Recall that the force on a current-carrying conductor in a magnetic field is given by →F=I(→L×→B).
Step 3: Analyze the Forces on the Other Arms
- Arm B: The current in this arm is parallel to the magnetic field. According to the Lorentz force law, the force on a current-carrying conductor is zero when the current is parallel to the magnetic field. Therefore, the force on arm B is 0.
- Arm C: The current in this arm flows in the opposite direction to arm A. By applying Fleming's left-hand rule, the force on arm C will be equal in magnitude but opposite in direction to the force on arm A. Thus, the force on arm C is −→F.
- Arm D: Similar to arm B, the current in arm D is also parallel to the magnetic field. Hence, the force on arm D is also 0.
Hint: Remember that forces on arms parallel to the magnetic field are zero.
Step 4: Calculate the Net Force on the Remaining Three Arms
Now we can sum up the forces on the remaining three arms (B, C, and D):
- Force on arm B = 0
- Force on arm C = −→F
- Force on arm D = 0
Thus, the net force →Fnet on the remaining three arms is:
→Fnet=0+(−→F)+0=−→F
Final Answer
The net force on the remaining three arms of the loop is −→F.
---
We have a square current-carrying loop suspended in a uniform magnetic field. The magnetic field is acting in the plane of the loop. Let's denote the arms of the loop as A, B, C, and D.
We are given that the force on one arm of the loop (let's say arm A) is →F. This force is due to the interaction of the magnetic field with the current flowing through that arm.
- Arm B: The current in this arm is parallel to the magnetic field. According to the Lorentz force law, the force on a current-carrying conductor is zero when the current is parallel to the magnetic field. Therefore, the force on arm B is 0.
- Arm C: The current in this arm flows in the opposite direction to arm A. By applying Fleming's left-hand rule, the force on arm C will be equal in magnitude but opposite in direction to the force on arm A. Thus, the force on arm C is −→F.
Now we can sum up the forces on the remaining three arms (B, C, and D):
- Force on arm B = 0
- Force on arm C = −→F
- Force on arm D = 0
→Fnet=0+(−→F)+0=−→F
The net force on the remaining three arms of the loop is −→F.
Similar Questions
A current carrying loop in a uniform magnetic field will experience
View Solutionthe net force on the loop is
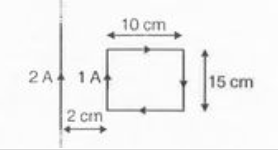
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
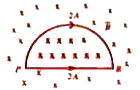
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
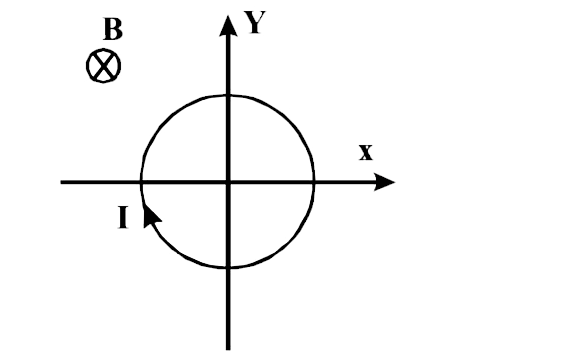
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
View SolutionA current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction
View SolutionA current loop in a magnetic field
View SolutionForce on current carrying loop (Radius = R) in uniform magnetic (B) field which is at an angle 30” with the normal will be :-
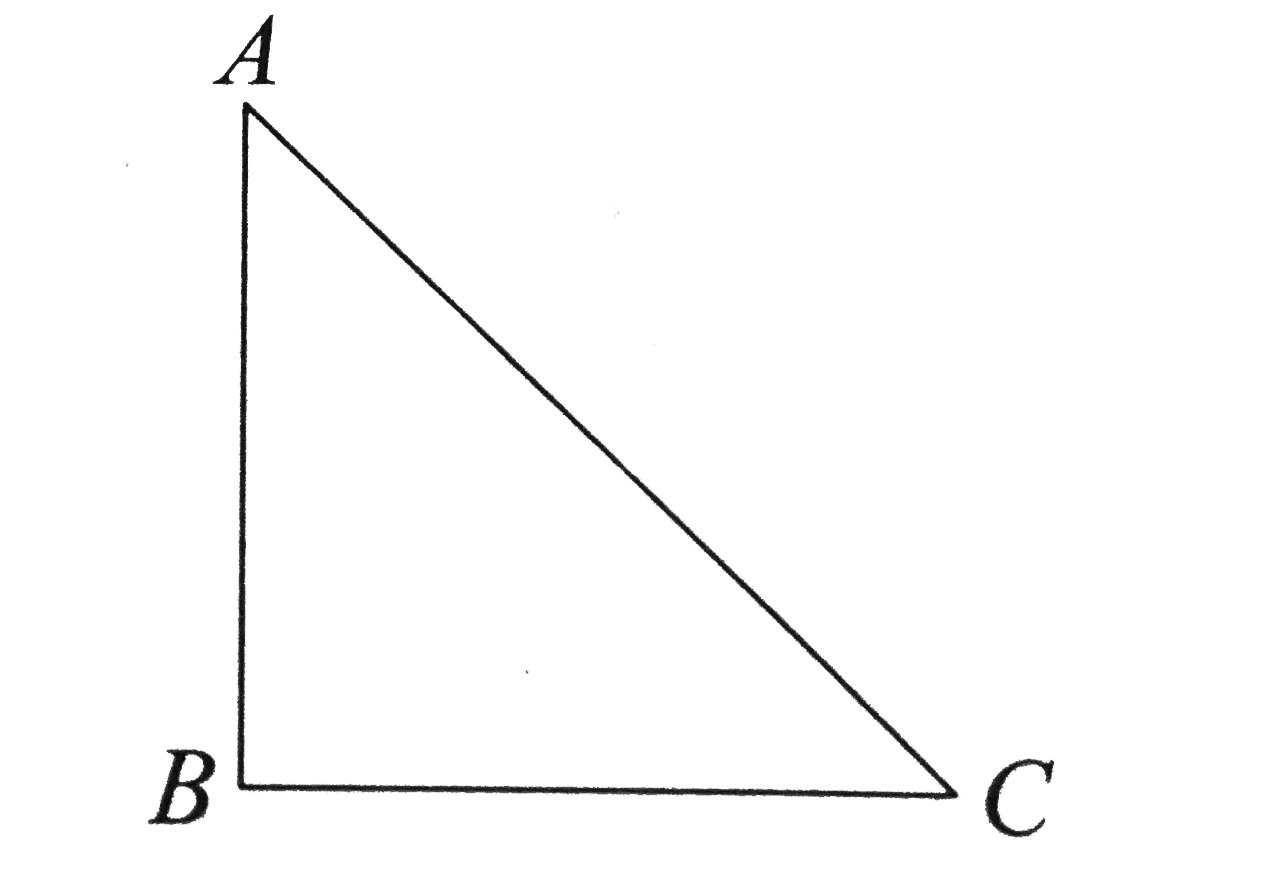
View SolutionA current carrying closed loop in the from of a right angle isoseles triangle ABC is placed in a unifrom magnetic fild acting along AB. If the magnetic force on the arm BC is F, the force on the arm AC is
View Solution