A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
mgcosθ
mgsinθ
mg
mgcosθ
The correct Answer is:D
To solve the problem, we need to analyze the forces acting on the block placed on the wedge. The wedge is inclined at an angle θ, and the entire system is accelerated horizontally. We will use Newton's laws of motion to derive the required force exerted by the wedge on the block.
1. Identify the Forces Acting on the Block:
- The gravitational force acting downward on the block is mg.
- The normal force exerted by the wedge on the block is R, which acts perpendicular to the surface of the wedge.
2. Resolve Forces into Components:
- Since the wedge is inclined at an angle θ, we can resolve the normal force R into two components:
- Horizontal component: Rsinθ
- Vertical component: Rcosθ
3. Apply Newton's Second Law in the Horizontal Direction:
- The block does not slip on the wedge, meaning it accelerates horizontally with the same acceleration A as the wedge.
- From the horizontal component of the forces, we have:
Rsinθ=mA(1)
4. Apply Newton's Second Law in the Vertical Direction:
- In the vertical direction, the block is in equilibrium because the only forces acting vertically are the weight of the block and the vertical component of the normal force.
- Thus, we have:
Rcosθ=mg(2)
5. Solve for the Normal Force R:
- From equation (2), we can express R in terms of mg:
R=mgcosθ
6. Conclusion:
- The force exerted by the wedge on the block is given by:
R=mgcosθ
Final Answer:
The force exerted by the wedge on the block is R=mgcosθ.
---
- The gravitational force acting downward on the block is mg.
- The normal force exerted by the wedge on the block is R, which acts perpendicular to the surface of the wedge.
- Since the wedge is inclined at an angle θ, we can resolve the normal force R into two components:
- Horizontal component: Rsinθ
- Vertical component: Rcosθ
- The block does not slip on the wedge, meaning it accelerates horizontally with the same acceleration A as the wedge.
- From the horizontal component of the forces, we have:
Rsinθ=mA(1)
- In the vertical direction, the block is in equilibrium because the only forces acting vertically are the weight of the block and the vertical component of the normal force.
- Thus, we have:
Rcosθ=mg(2)
- From equation (2), we can express R in terms of mg:
R=mgcosθ
- The force exerted by the wedge on the block is given by:
R=mgcosθ
The force exerted by the wedge on the block is R=mgcosθ.
Similar Questions
A block of mass m is placed on a smooth wedge of incination θ. The whole system s acelerated horizontally so tht the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
View SolutionA block of mass m is placed on a smooth wedge of inclination Q. The whole system is accelerated horizontally so that the block does not slip on the wedge. Find the
i) Acceleration of the wedge
ii) Force to be applied on the wedge
iii) Force exerted by the wedge on the block.
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA small block of mass m is kept on a rough inclined surface of inclination θ fixed in a car. The car moves with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
_PHY_E05_250_Q01.png)
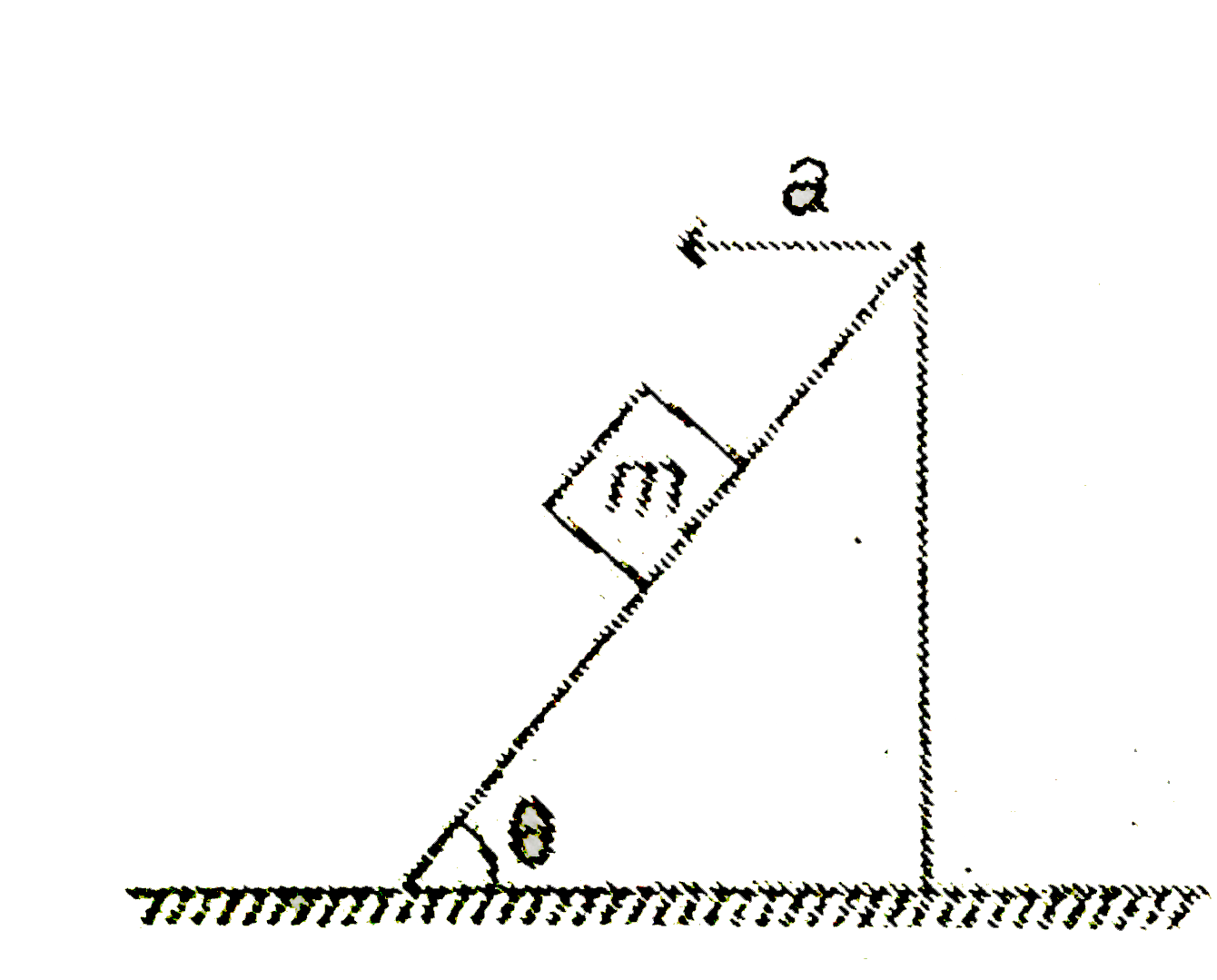
View SolutionAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
View SolutionA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is

View SolutionAll surfaces are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
