A block of mass m is placed on a smooth wedge of incination θ. The whole system s acelerated horizontally so tht the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
mg
mgcosθ
mgcosθ
mgtanθ
The correct Answer is:B
To solve the problem of finding the force exerted by the wedge on the block, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
The block of mass m experiences the following forces:
- Gravitational Force (Weight): →W=mg acting downward.
- Normal Force (N): Exerted by the wedge, acting perpendicular to the surface of the wedge.
- Pseudoforce (F_p): Since the system is accelerating horizontally, a pseudoforce acts on the block in the opposite direction of the acceleration a.
Step 2: Analyze the Forces in the Inclined Plane Coordinates
We will resolve the forces into components parallel and perpendicular to the inclined plane:
- The gravitational force can be resolved into:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
- The pseudoforce can also be resolved:
- Perpendicular to the incline: Fp⊥=masinθ
- Parallel to the incline: Fp∥=macosθ
Step 3: Apply the Equilibrium Conditions
Since the block does not slip, it is in equilibrium in both the directions parallel and perpendicular to the incline.
For the parallel direction:
ΣF∥=0⟹mgsinθ−macosθ=0
From this, we can derive:
mgsinθ=macosθ⟹a=gsinθcosθ=gtanθ
For the perpendicular direction:
\Sigma F_{\perpendicular} = 0 \implies N - mg \cos \theta - ma \sin \theta = 0
Substituting a from the previous result:
N=mgcosθ+m(gtanθ)sinθ
This simplifies to:
N=mgcosθ+mgsin2θ
Step 4: Simplify the Expression for Normal Force
Using the identity sin2θ+cos2θ=1:
N=mg(cos2θ+sin2θ)=mg
Thus, we can express N as:
N=mgcosθ
Final Answer
The force exerted by the wedge on the block is:
N=mgcosθ
The block of mass m experiences the following forces:
- Gravitational Force (Weight): →W=mg acting downward.
- Normal Force (N): Exerted by the wedge, acting perpendicular to the surface of the wedge.
- Pseudoforce (F_p): Since the system is accelerating horizontally, a pseudoforce acts on the block in the opposite direction of the acceleration a.
We will resolve the forces into components parallel and perpendicular to the inclined plane:
- The gravitational force can be resolved into:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: Fp⊥=masinθ
- Parallel to the incline: Fp∥=macosθ
Since the block does not slip, it is in equilibrium in both the directions parallel and perpendicular to the incline.
ΣF∥=0⟹mgsinθ−macosθ=0
From this, we can derive:
mgsinθ=macosθ⟹a=gsinθcosθ=gtanθ
\Sigma F_{\perpendicular} = 0 \implies N - mg \cos \theta - ma \sin \theta = 0
Substituting a from the previous result:
N=mgcosθ+m(gtanθ)sinθ
This simplifies to:
N=mgcosθ+mgsin2θ
Using the identity sin2θ+cos2θ=1:
N=mg(cos2θ+sin2θ)=mg
Thus, we can express N as:
N=mgcosθ
The force exerted by the wedge on the block is:
N=mgcosθ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
9 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - worked out Examples
11 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
View SolutionA block of mass m is placed on a smooth wedge of inclination Q. The whole system is accelerated horizontally so that the block does not slip on the wedge. Find the
i) Acceleration of the wedge
ii) Force to be applied on the wedge
iii) Force exerted by the wedge on the block.
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
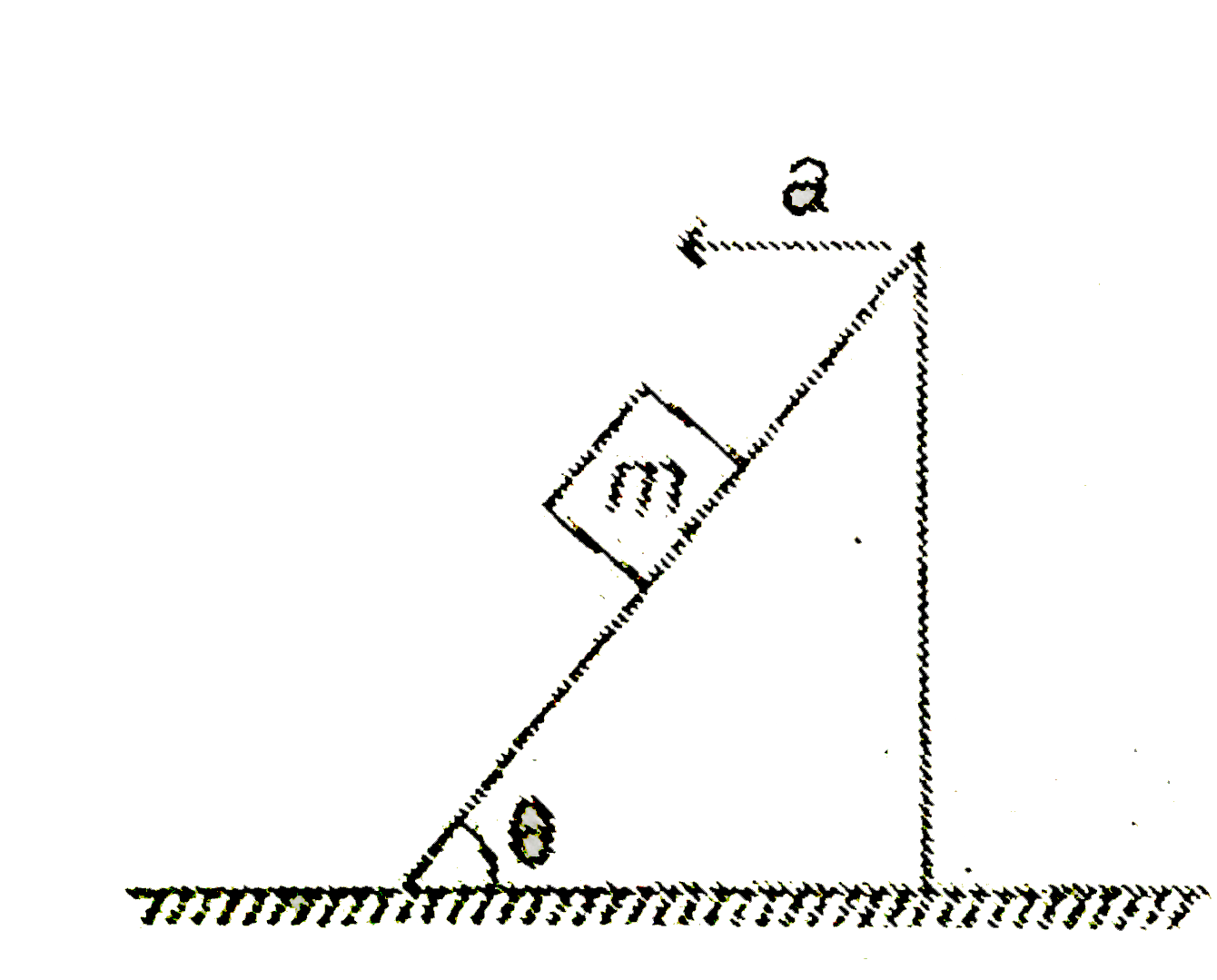
View SolutionAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionAll surfaces are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View Solution
