Which of the following transitions in a hydrogen atom emits photon of the highest frequency ?
n = 1 to n = 2
n = 2 to n = 1
n = 2 to n = 6
n = 6 to n = 2
The correct Answer is:B
To determine which transition in a hydrogen atom emits a photon of the highest frequency, we can follow these steps:
Step 1: Understand the Concept of Energy Levels
In a hydrogen atom, electrons occupy discrete energy levels, denoted by quantum numbers (n). The energy of these levels increases with n. A transition from a higher energy level (higher n) to a lower energy level (lower n) results in the emission of a photon.
Step 2: Identify the Given Transitions
We need to analyze the transitions provided in the options. Let's denote them as follows:
1. Transition from n = 2 to n = 1
2. Transition from n = 3 to n = 1
3. Transition from n = 4 to n = 2
4. Transition from n = 6 to n = 2
Step 3: Use the Formula for Frequency of Emitted Photon
The frequency (f) of the emitted photon during a transition can be calculated using the formula:
f=R⋅c(1n2final−1n2initial)
where R is the Rydberg constant and c is the speed of light.
Step 4: Calculate Frequency for Each Transition
1. For n = 2 to n = 1:
f1=R⋅c(112−122)=R⋅c(1−14)=R⋅c⋅34
2. For n = 3 to n = 1:
f2=R⋅c(112−132)=R⋅c(1−19)=R⋅c⋅89
3. For n = 4 to n = 2:
f3=R⋅c(122−142)=R⋅c(14−116)=R⋅c⋅316
4. For n = 6 to n = 2:
f4=R⋅c(122−162)=R⋅c(14−136)=R⋅c(9−136)=R⋅c⋅836=R⋅c⋅29
Step 5: Compare the Frequencies
Now we compare the calculated frequencies:
- f1=R⋅c⋅34
- f2=R⋅c⋅89
- f3=R⋅c⋅316
- f4=R⋅c⋅29
Step 6: Determine the Highest Frequency
To find the highest frequency, we can compare the fractions:
- 34 is approximately 0.75
- 89 is approximately 0.89
- 316 is approximately 0.1875
- 29 is approximately 0.2222
The highest frequency corresponds to the transition from n = 3 to n = 1, which is f2.
Conclusion
The transition in a hydrogen atom that emits a photon of the highest frequency is from n = 3 to n = 1.
---
In a hydrogen atom, electrons occupy discrete energy levels, denoted by quantum numbers (n). The energy of these levels increases with n. A transition from a higher energy level (higher n) to a lower energy level (lower n) results in the emission of a photon.
We need to analyze the transitions provided in the options. Let's denote them as follows:
1. Transition from n = 2 to n = 1
2. Transition from n = 3 to n = 1
3. Transition from n = 4 to n = 2
4. Transition from n = 6 to n = 2
The frequency (f) of the emitted photon during a transition can be calculated using the formula:
f=R⋅c(1n2final−1n2initial)
where R is the Rydberg constant and c is the speed of light.
1. For n = 2 to n = 1:
f1=R⋅c(112−122)=R⋅c(1−14)=R⋅c⋅34
f2=R⋅c(112−132)=R⋅c(1−19)=R⋅c⋅89
f3=R⋅c(122−142)=R⋅c(14−116)=R⋅c⋅316
f4=R⋅c(122−162)=R⋅c(14−136)=R⋅c(9−136)=R⋅c⋅836=R⋅c⋅29
Now we compare the calculated frequencies:
- f1=R⋅c⋅34
- f2=R⋅c⋅89
- f3=R⋅c⋅316
- f4=R⋅c⋅29
To find the highest frequency, we can compare the fractions:
- 34 is approximately 0.75
- 89 is approximately 0.89
- 316 is approximately 0.1875
- 29 is approximately 0.2222
The transition in a hydrogen atom that emits a photon of the highest frequency is from n = 3 to n = 1.
Similar Questions
Knowledge Check
Which of the transitions in hydrogen atom emits a photon of lowest frequecny (n= quantum number)?
An=2 to n=1Bn=4 to n=2Cn=4 to n=1Dn=4 to n=3
In which transition of a hydrogen atom, photons of lowest frequency are emitted ?
View SolutionWhich of the following transitions gives photon of maximum energy
View SolutionWhich of the following electronic transition in hydrogen atom will emit largest amount of energy?
View SolutionWhich of the following transition will emit maximum energy in hydrogen atom ?
View SolutionWhenever a hydrogen atom emits a photon in the Balmer series .
View SolutionIn figure E1andE2 represent some of the energy levels of the hydrogen atom.
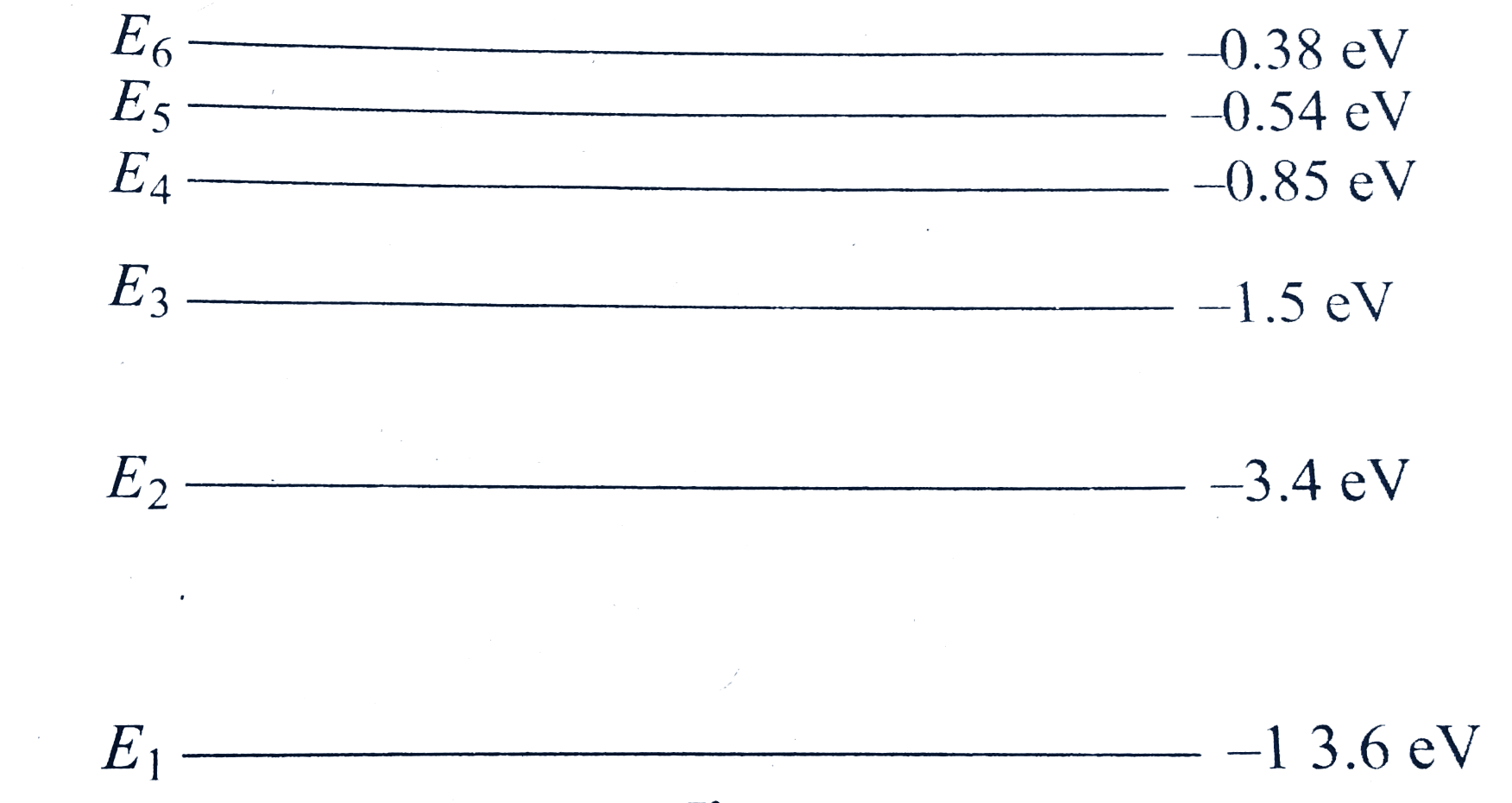
Which one of the following transitions produced a photon of wavelength in the ultraviolet region of the electromagnetic spectrum?
View SolutionWhich electronic transition in a hydrogen atom releases the greatest amount of energy?
View Solution