A body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton's law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be
74T
32T
43T
T
The correct Answer is:B
To solve the problem, we will apply Newton's law of cooling, which states that the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature.
1. Identify Initial Conditions:
- Initial temperature of the body, θ1=3T
- Final temperature after 10 minutes, θ2=2T
- Room temperature (ambient temperature), θs=T
- Time interval, t=10 minutes
2. Apply Newton's Law of Cooling:
According to Newton's law of cooling:
dθdt=−k(θ−θs)
where k is a constant.
3. Calculate the Average Temperature:
The average temperature of the body during the cooling process from 3T to 2T is:
θavg=θ1+θ22=3T+2T2=5T2
4. Set Up the Cooling Equation:
Using the temperatures and the time interval:
2T−3T10=−k(5T2−T)
Simplifying the left side:
−T10=−k(5T2−T)
The right side simplifies to:
5T2−T=5T2−2T2=3T2
Thus, we have:
−T10=−k(3T2)
5. Solve for k:
Rearranging gives:
k=T/103T/2=110⋅23=115
6. Determine the Temperature After the Next 10 Minutes:
Now, we need to find the temperature after another 10 minutes, starting from 2T:
- New initial temperature θ2=2T
- We will use the same ambient temperature T and the same k.
The average temperature during this cooling period is:
θavg=2T+θf2
where θf is the final temperature we want to find.
The cooling equation becomes:
θf−2T10=−k(2T+θf2−T)
Simplifying the right side:
θf−2T10=−115(2T+θf2−T)
=−115(2T+θf−2T2)=−115(θf2)
Thus, we have:
θf−2T10=−θf30
7. Cross-Multiply and Solve for θf:
Cross-multiplying gives:
3(θf−2T)=−θf
3θf−6T=−θf
4θf=6T
θf=6T4=3T2
Final Answer:
The temperature of the body at the end of the next 10 minutes will be 3T2.
- Initial temperature of the body, θ1=3T
- Final temperature after 10 minutes, θ2=2T
- Room temperature (ambient temperature), θs=T
- Time interval, t=10 minutes
According to Newton's law of cooling:
dθdt=−k(θ−θs)
where k is a constant.
The average temperature of the body during the cooling process from 3T to 2T is:
θavg=θ1+θ22=3T+2T2=5T2
Using the temperatures and the time interval:
2T−3T10=−k(5T2−T)
Simplifying the left side:
−T10=−k(5T2−T)
The right side simplifies to:
5T2−T=5T2−2T2=3T2
Thus, we have:
−T10=−k(3T2)
Rearranging gives:
k=T/103T/2=110⋅23=115
Now, we need to find the temperature after another 10 minutes, starting from 2T:
- New initial temperature θ2=2T
- We will use the same ambient temperature T and the same k.
θavg=2T+θf2
where θf is the final temperature we want to find.
θf−2T10=−k(2T+θf2−T)
Simplifying the right side:
θf−2T10=−115(2T+θf2−T)
=−115(2T+θf−2T2)=−115(θf2)
Thus, we have:
θf−2T10=−θf30
Cross-multiplying gives:
3(θf−2T)=−θf
3θf−6T=−θf
4θf=6T
θf=6T4=3T2
The temperature of the body at the end of the next 10 minutes will be 3T2.
Similar Questions
A body cools from 60∘C to 50∘C in 10 min. Find its temperature at the end of next 10 min if the room temperature is 25∘C. Assume Newton's law of cooling holds.
View SolutionA body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View SolutionA body having mass 2 Kg cools in a surrounding of constant temperature 30∘C. Its heat capacity is 2J/∘C. Initial temperature of the body is 40∘C. Assume Newton's law of cooling is valid. The body cools to 36∘C in 10 minutes.
When the body temperature has reached 36∘C. it is heated again so that it reaches to 40∘C in 10 minutes. Assume that the rate of loss of heat at 38∘C is the average rate of loss for the given time . The total heat required from a heater by the body is :
View SolutionIf a body cools down from 80∘Cto 60∘C in 10 min when the temperature of the surrounding of the is 30∘C . Then, the temperature of the body after next 10 min will be
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
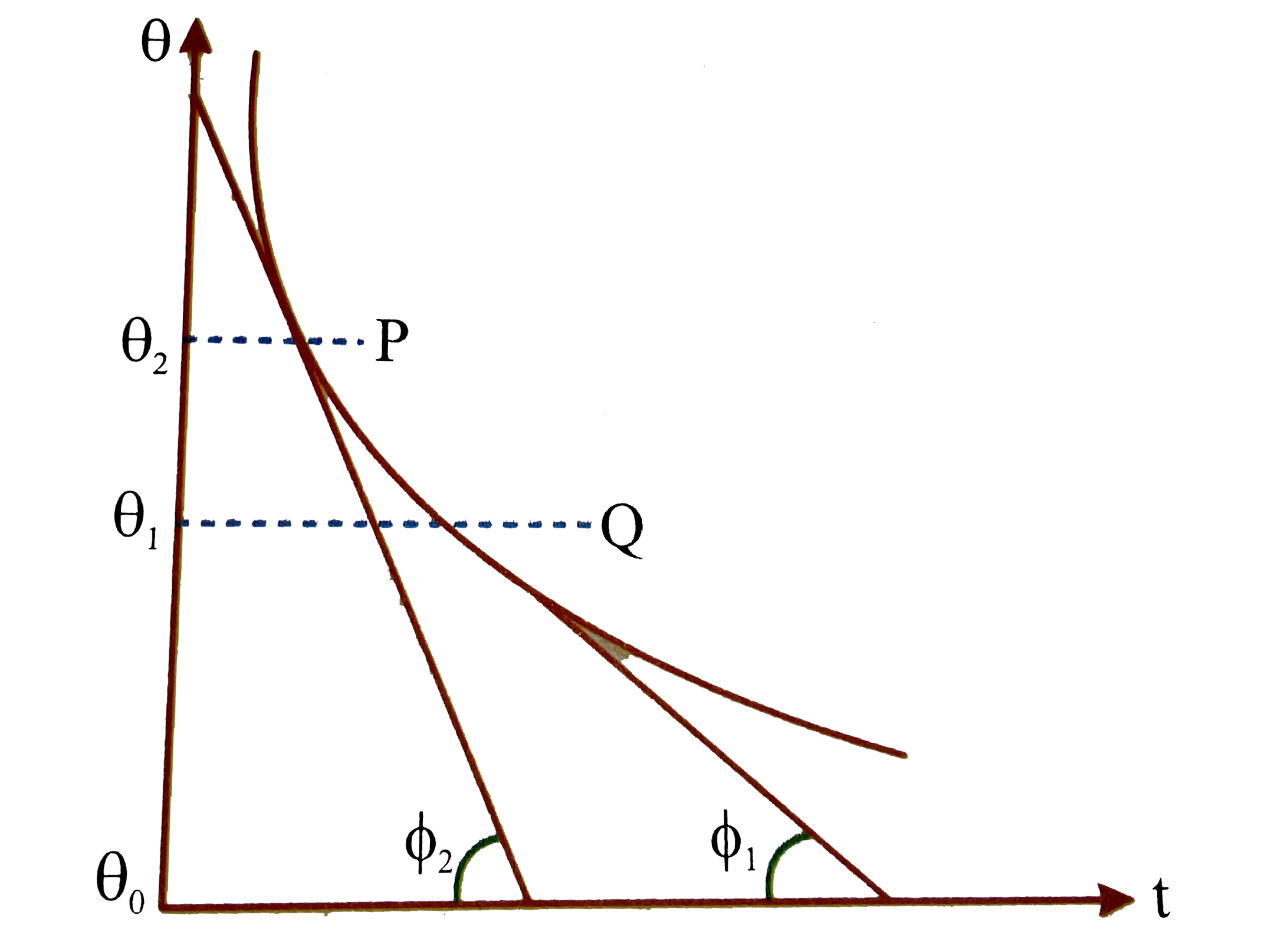
View SolutionA body cools in a surrounding of constant temperature 30∘C. Its heat capacity is 2J/∘C. Initial temperature of the body is 40∘C. Assume Newton's law of cooling is valid. The body cools to 36∘C in 10 minutes.
In further 10 minutes it will cool from 36∘C to :
View SolutionA body cools from 50∘C to 40∘C in 5 min. If the temperature of the surrounding is 20∘C , the temperature of the body after the next 5 min would be
View SolutionState Newton's law of cooling and draw the graph showing cooling of hot water with temperature.
View SolutionA solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
View SolutionA body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temeprature of cooling is 40∘C and assuming newtons law of cooling is valid. The body cools to 38∘C in 10 min
In further 10 min it will cools from 38∘C to _____
View Solution
