A capacitor is charge until it stores an energy of 1J. A second uncharged capacitor is connected to it, so that charge districutes equally. The final energy stored in the second capacitor is
1J
0.5J
0.25J
0.125J
The correct Answer is:3
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Initial Condition
We have a capacitor (let's call it C1) that is charged to store an energy of 1 Joule. The energy stored in a capacitor can be expressed using the formula:
U=Q22C
where U is the energy stored, Q is the charge, and C is the capacitance.
Step 2: Relate Energy to Charge and Capacitance
From the given information, we can set up the equation:
Q22C1=1(1)
This equation relates the charge Q on the capacitor C1 to its capacitance C1.
Step 3: Connect the Second Capacitor
Now, a second uncharged capacitor (C2) is connected to C1. When they are connected, the charge will redistribute equally between the two capacitors. Assuming that both capacitors have the same capacitance C1=C2, the total charge Q will be shared equally:
Q1=Q2andQ2=Q2
where Q1 is the charge on C1 and Q2 is the charge on C2 after redistribution.
Step 4: Calculate the Energy Stored in the Second Capacitor
The energy stored in the second capacitor (C2) can be calculated using the same energy formula:
U2=Q222C2
Substituting Q2=Q2 and C2=C1:
U2=(Q2)22C1
U2=Q2/42C1=Q28C1(2)
Step 5: Substitute from Equation (1)
From equation (1), we know:
Q22C1=1⟹Q2=2C1
Now substitute Q2 into equation (2):
U2=2C18C1=28=14(3)
Step 6: Final Result
Thus, the final energy stored in the second capacitor is:
U2=0.25 Joules
Conclusion
The final energy stored in the second capacitor after charge redistribution is 0.25 Joules.
---
We have a capacitor (let's call it C1) that is charged to store an energy of 1 Joule. The energy stored in a capacitor can be expressed using the formula:
U=Q22C
where U is the energy stored, Q is the charge, and C is the capacitance.
From the given information, we can set up the equation:
Q22C1=1(1)
This equation relates the charge Q on the capacitor C1 to its capacitance C1.
Now, a second uncharged capacitor (C2) is connected to C1. When they are connected, the charge will redistribute equally between the two capacitors. Assuming that both capacitors have the same capacitance C1=C2, the total charge Q will be shared equally:
Q1=Q2andQ2=Q2
where Q1 is the charge on C1 and Q2 is the charge on C2 after redistribution.
The energy stored in the second capacitor (C2) can be calculated using the same energy formula:
U2=Q222C2
Substituting Q2=Q2 and C2=C1:
U2=(Q2)22C1
U2=Q2/42C1=Q28C1(2)
From equation (1), we know:
Q22C1=1⟹Q2=2C1
Now substitute Q2 into equation (2):
U2=2C18C1=28=14(3)
Thus, the final energy stored in the second capacitor is:
U2=0.25 Joules
The final energy stored in the second capacitor after charge redistribution is 0.25 Joules.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
The energy stored in 4μF capacitors is
View SolutionMatch the columns

View SolutionFind the charge stored in the capacitor.
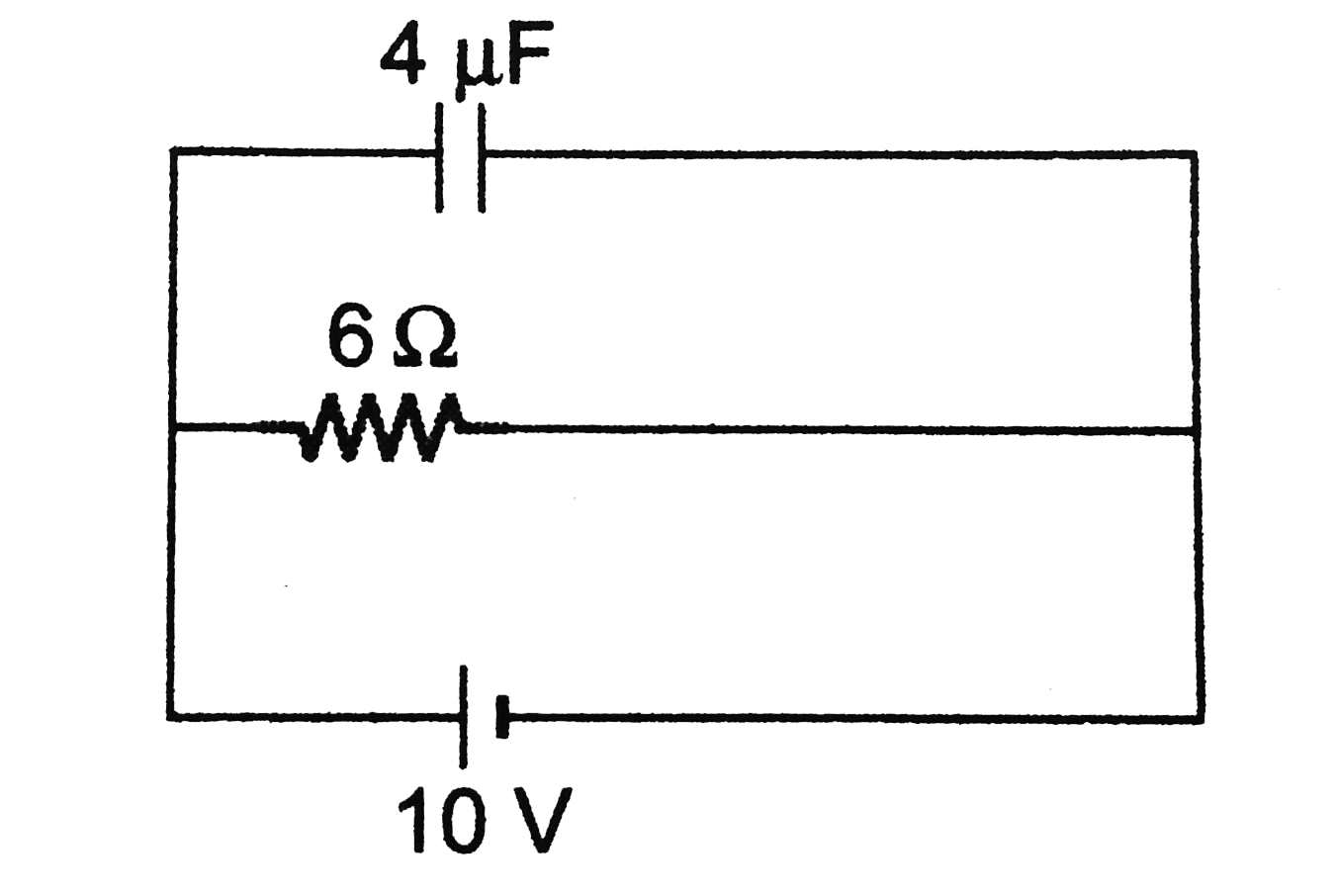
View SolutionFind the charge stored in the capacitor.
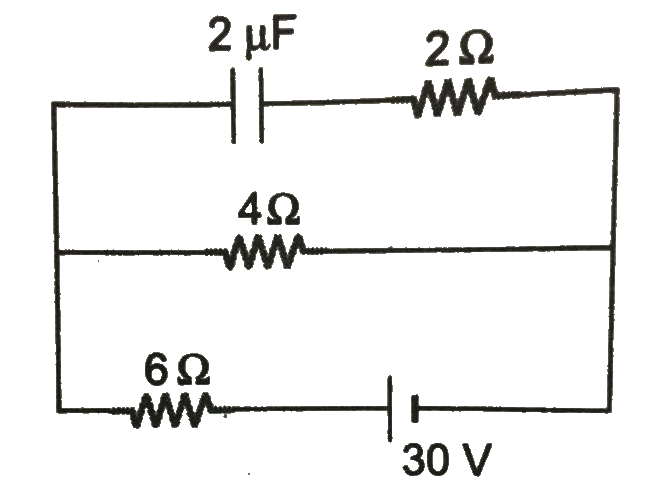
View SolutionFind the charge stored in the capacitor.
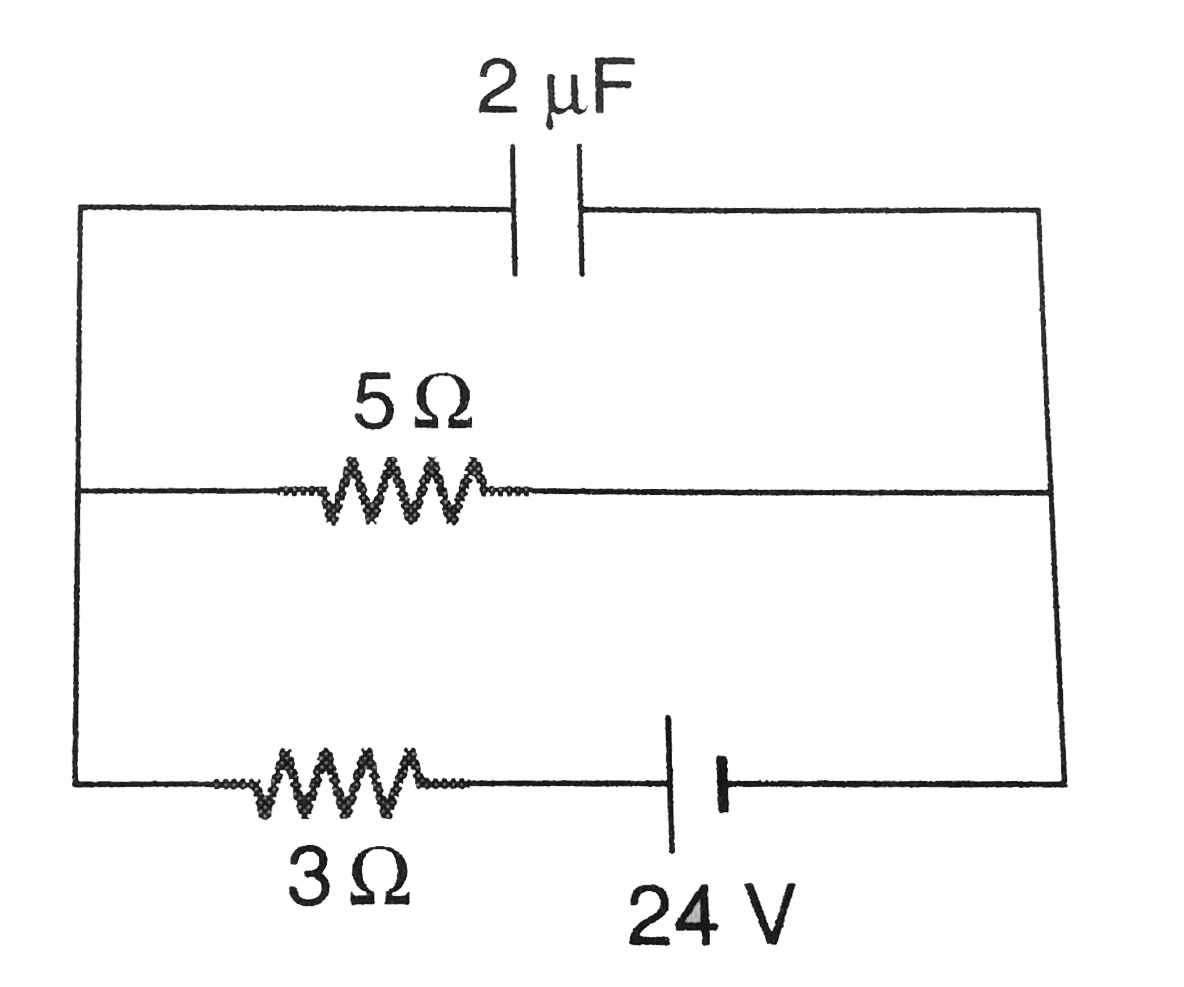
View SolutionFind the charged stored in all the capacitors
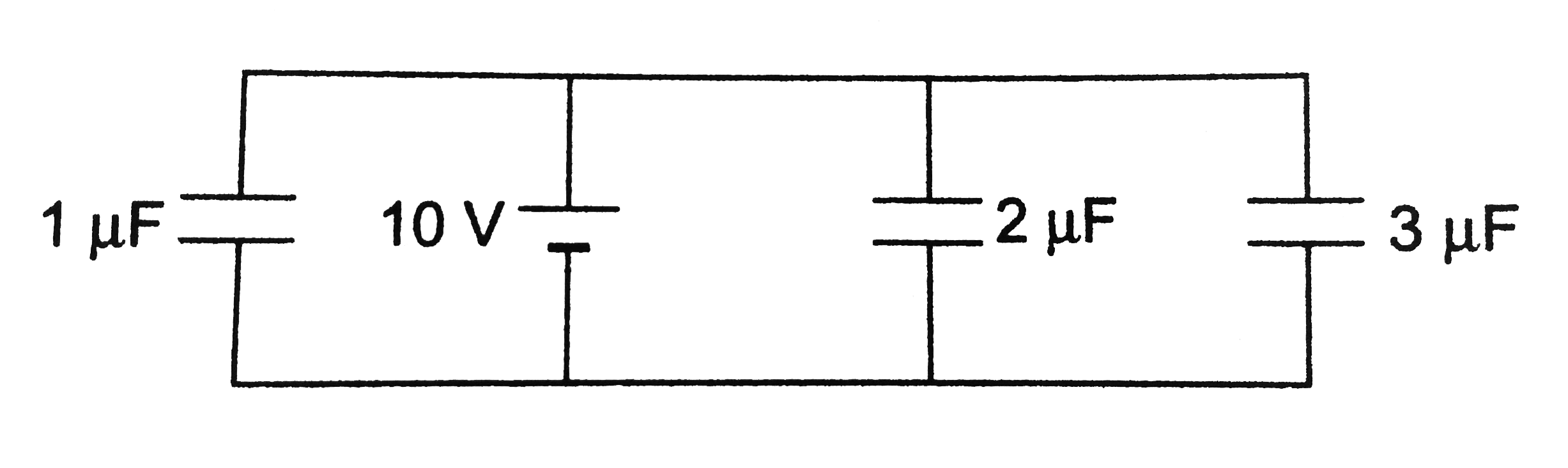
View SolutionThe total electrostatic energy stored in both the capacitor is
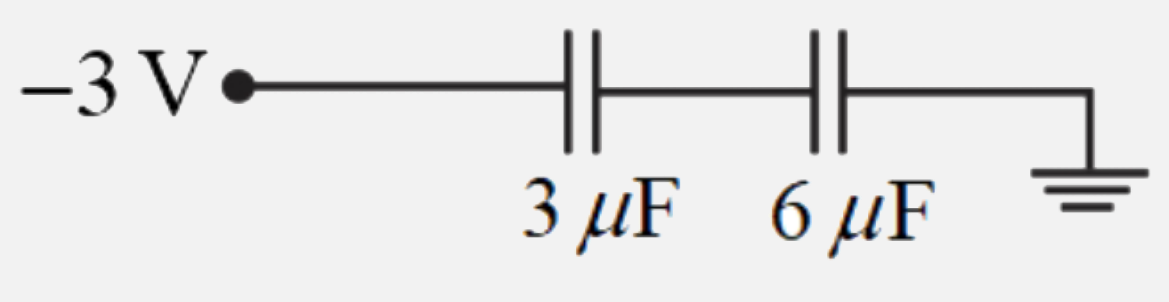
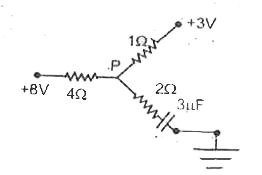
View SolutionThe energy stored in the capacitor in the steady state is
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
View Solution

