What is the flux through a cube of side 'a' if a point charge of q is at one of its corner :
q∈0
q2∈06a2
2q∈0
q8∈0
The correct Answer is:D
To find the electric flux through a cube of side 'a' when a point charge 'q' is placed at one of its corners, we can follow these steps:
1. Understand the Setup:
- We have a cube with side length 'a'.
- A point charge 'q' is located at one of the corners of the cube.
2. Apply Gauss's Law:
- Gauss's Law states that the electric flux (Φ) through a closed surface is equal to the charge enclosed (Q_enc) divided by the permittivity of free space (ε₀):
Φ=Qencϵ0
3. Determine the Charge Enclosed:
- Since the charge 'q' is located at one corner of the cube, we need to determine how much of this charge is effectively enclosed by the cube.
- The cube can be thought of as occupying one of the eight equal parts of space around the charge at the corner. Therefore, only 1/8 of the charge 'q' is enclosed by the cube.
4. Calculate the Enclosed Charge:
- The enclosed charge (Q_enc) by the cube is:
Qenc=q8
5. Substitute into Gauss's Law:
- Now, substituting the value of Q_enc into Gauss's Law gives:
Φ=Qencϵ0=q8ϵ0=q8ϵ0
6. Final Answer:
- Therefore, the electric flux through the cube is:
Φ=q8ϵ0
Conclusion:
The flux through the cube of side 'a' when a point charge 'q' is at one of its corners is given by:
Φ=q8ϵ0
- We have a cube with side length 'a'.
- A point charge 'q' is located at one of the corners of the cube.
- Gauss's Law states that the electric flux (Φ) through a closed surface is equal to the charge enclosed (Q_enc) divided by the permittivity of free space (ε₀):
Φ=Qencϵ0
- Since the charge 'q' is located at one corner of the cube, we need to determine how much of this charge is effectively enclosed by the cube.
- The cube can be thought of as occupying one of the eight equal parts of space around the charge at the corner. Therefore, only 1/8 of the charge 'q' is enclosed by the cube.
- The enclosed charge (Q_enc) by the cube is:
Qenc=q8
- Now, substituting the value of Q_enc into Gauss's Law gives:
Φ=Qencϵ0=q8ϵ0=q8ϵ0
- Therefore, the electric flux through the cube is:
Φ=q8ϵ0
The flux through the cube of side 'a' when a point charge 'q' is at one of its corners is given by:
Φ=q8ϵ0
Similar Questions
The total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is
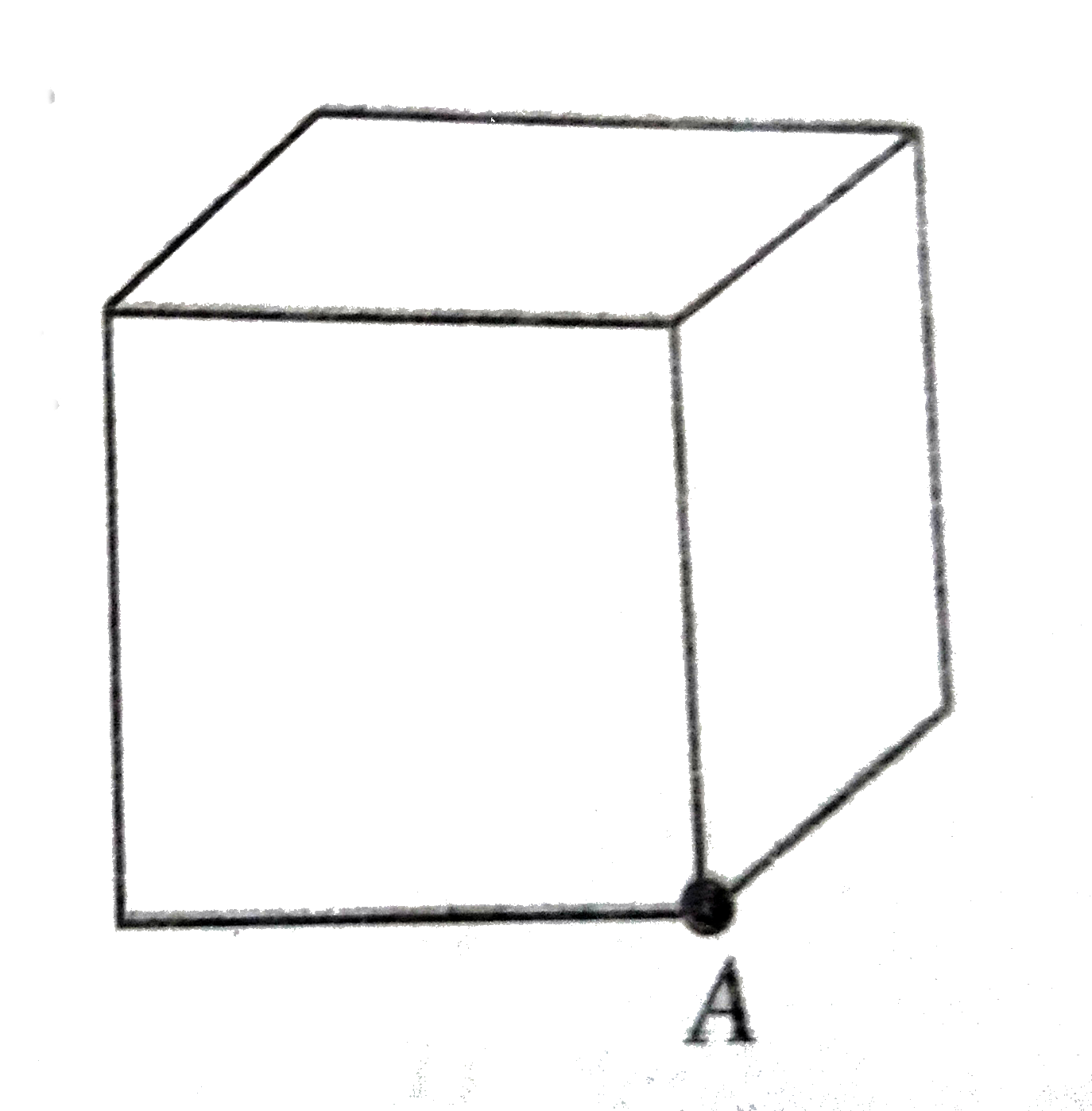 View Solution
View SolutionIn figure, a charge q is placed at a distance δ→0 near one of the corners of a cube of edge I on a line of symmetry along diagonal.

1. What is the flux through each of the faces containing the point a?
2. What is the flux through the other three faces?View SolutionConsider a cube ABCGHIJK of sides a placed in a uniform magnetic field B acting perpendicular to the face BHIC as shown in figure.
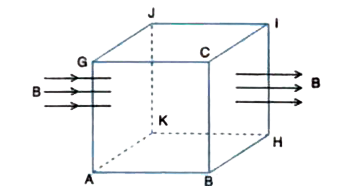
(i) What is the flux through face ABCG?
(ii) What is the flux through face GCIJ?
(iii) What is the flux through face AKJG?
(iv) What is the flux through face BHIC?View SolutionWhat will be the total flux through the faces of the cube, with side of length a if a charge q is placed at (a) A : a corner of the cube (b) B : mid-point of an edge of the cube (c ) C : center of a face of the cube (d) D : mid-point of B and C.
View SolutionThe length of each side of a cubical closed surface is L metre. If charge 48C is situated at one of the corners of the cube, Find the flux passing through the cube. (In Volt-metre)
View SolutionPoint charges +qand−q are kept alternately at the corners of a cube of side 'a' as shown in the figure. Write an expression for the work done in removing all the charges far away from each other.
 View Solution
View SolutionWhat is the net flux of the uniform electric field of the above question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
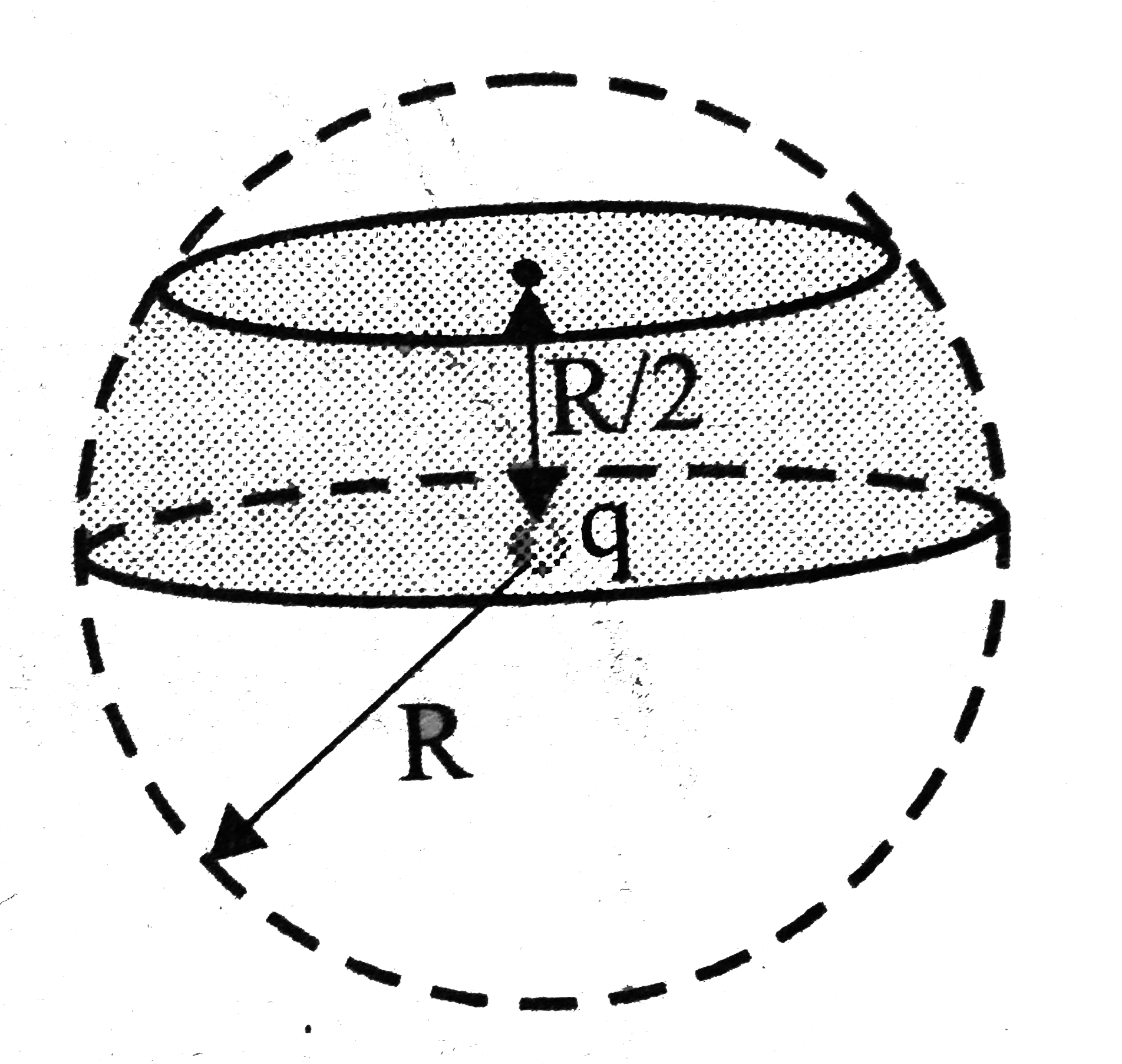 View Solution
View SolutionA charge is placed at the centre of cube of side a then flux linked with one of its given faces will be
View SolutionFive charges, q each are placed at the coreners of a regular pentagone of side.

(a) (i) What will be the electric field at O, the centre of the pentagon ?
(ii) What will be the electric field 0 if the charge from one of the corners (say A) is removed ?
(iii) What will be the electric field at 0 if the charge q at A is replaced by −q ?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its coreners ?View Solution

