In figure, a charge q is placed at a distance δ→0 near one of the corners of a cube of edge I on a line of symmetry along diagonal.

1. What is the flux through each of the faces containing the point a?
2. What is the flux through the other three faces?
Use of symmetry consideration may be useful in problems of flux calculation.

⋅ We can imagine a charged particle placed at the center of a cube of side 2l.
⋅ The flux enclosed with the cube is ϕ=q/ε0
⋅ The flux passing through on of the faces of the cube ϕ'=ϕ/6=q/6ε0
⋅ Hence, the flux passing through the face bcgf is ϕ'/4=q/24ε0
⋅ Each of the faces (efgh),(bcgh), and (dcgh) is symmetrical with respect to charge. Hence, the flux passing through each of the face is q/24ε0
The electric field lines for the faces (efgh),(bcgf) and (dcgh) are away from the faces. Hence, the flux associated with each of the faces will be positive (i.e.,+q/24ε0). Hence, the total flux through these sides is
3×q24ε0=q8ε0
⋅ As δ→0, we can say the faces (abcd),(avfe) and (adhe) are also symmetrical about charge. Charge is slightly outside the cube.
⋅ The number of electric field lines passing through the faces, which do not contain the point a, is same as the number of electric field lines passing through the faces containing the point a.
⋅ Hence, the same amount of flux will pass through the faces containing the point a, i.e., q/8ε0.
⋅ The electric field lines are toward the faces containing the point a. Hence, the flux will be negative, i.e., ϕ=−q8ε0.
Hence, the flux through each of the faces containing the point 'a' will be ϕ/3=q/24ε0.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Example
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.1
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 15 Videos
Similar Questions
What is the flux through a cube of side 'a' if a point charge of q is at one of its corner :
View SolutionA point charge q is placed at a distance a/2 directly above the centre of a square of side a. The electric flux through the square is
View SolutionCharge of 2 C is placed at the centre of a cube. What is the electric flux passing through one face ?
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
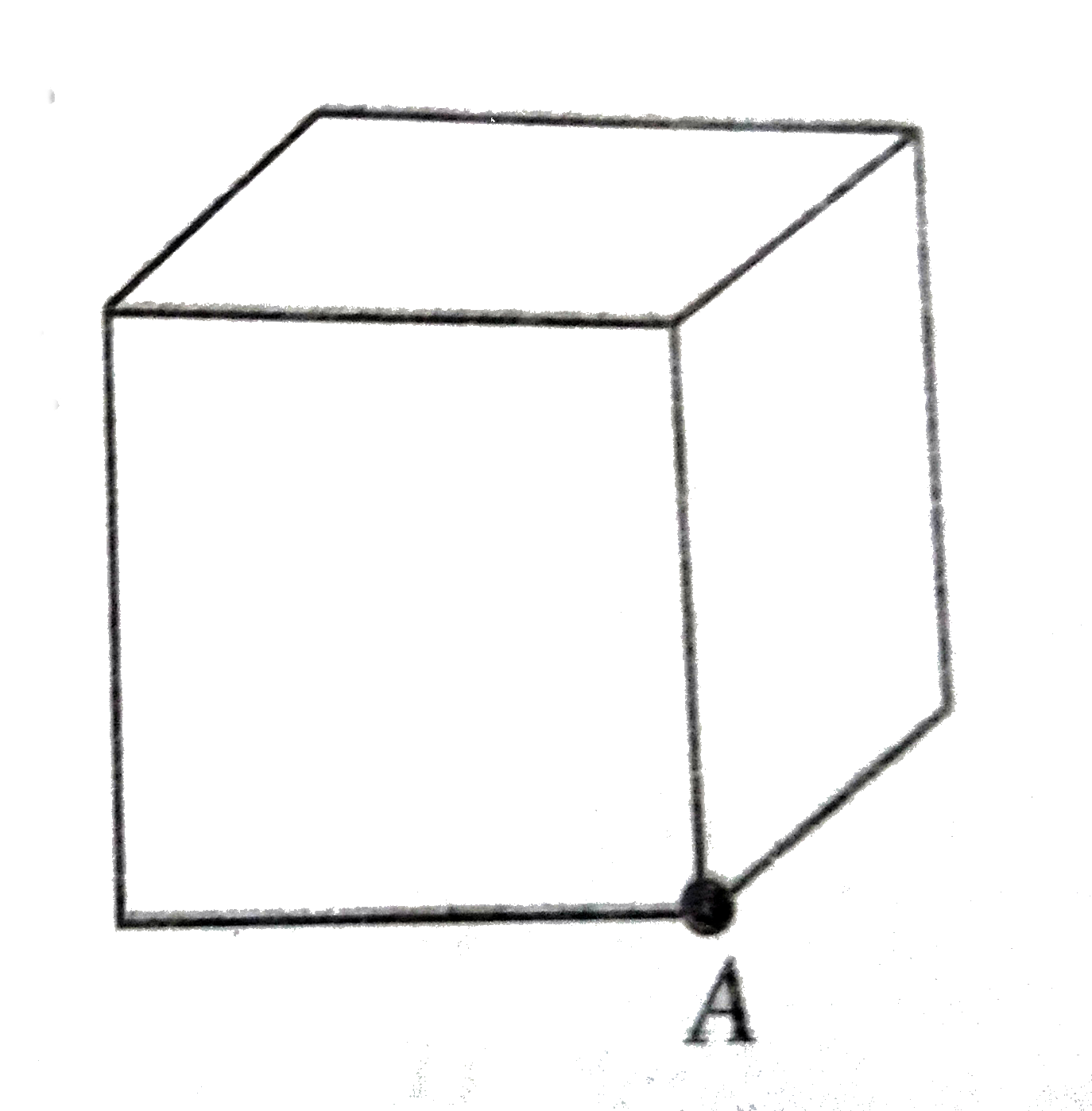
View SolutionThe total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is
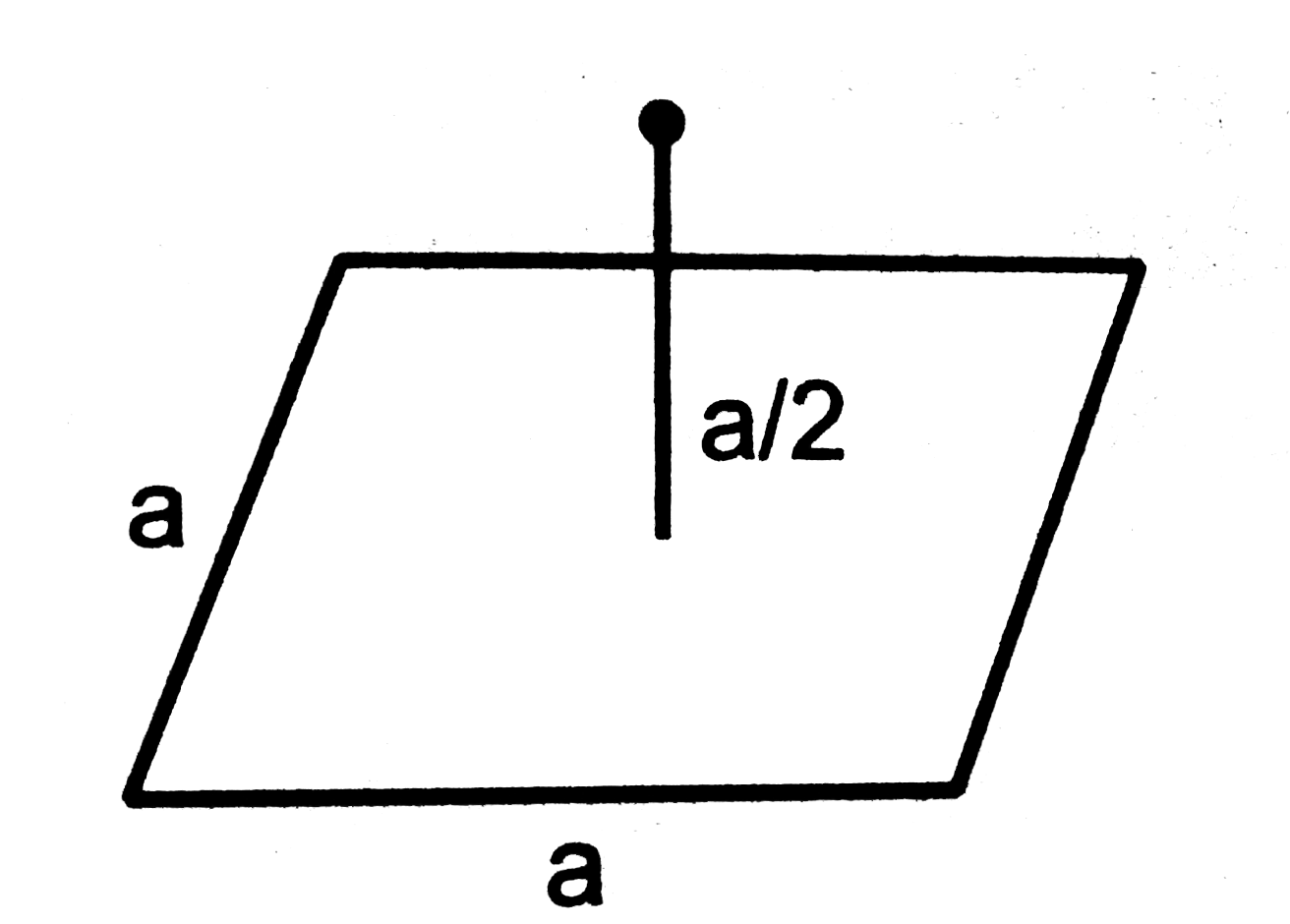
View SolutionA charge Q is placed at a distance a2 above the centre of a horizontal, spuare surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.
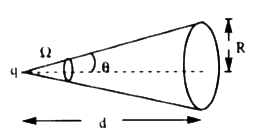
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
View SolutionIf charges q/2 and 2q are placed at the centre of face and at the corner of a cube, then the total flux through the cube will be
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View Solution
