Identify function which represent periodic motion
eωt
loge(ωt)
sin(ωt)+cos(ωt)
e−ωt
The correct Answer is:C
To identify which function represents periodic motion, we need to analyze each of the given functions one by one. A function is considered periodic if it repeats its values at regular intervals, known as the period.
1. Analyze the first function: eωt
- The function eωt is an exponential function.
- As t increases, eωt continuously increases and does not return to any previous value.
- Therefore, eωt is not periodic.
2. Analyze the second function: log(eωt)
- The function can be simplified to ωt since log(ex)=x.
- This function is a linear function that continuously increases without repeating any values.
- Thus, log(eωt) is not periodic.
3. Analyze the third function: sin(ωt)+cos(ωt)
- Both sin(ωt) and cos(ωt) are well-known periodic functions with a period of 2π.
- The sum of two periodic functions (with the same period) is also periodic.
- Therefore, sin(ωt)+cos(ωt) is periodic.
4. Analyze the fourth function: e−ωt
- Similar to the first function, e−ωt is also an exponential function.
- As t increases, e−ωt continuously decreases and does not return to any previous value.
- Hence, e−ωt is not periodic.
Conclusion:
From the analysis, the only function that represents periodic motion is:
- sin(ωt)+cos(ωt)
- The function eωt is an exponential function.
- As t increases, eωt continuously increases and does not return to any previous value.
- Therefore, eωt is not periodic.
- The function can be simplified to ωt since log(ex)=x.
- This function is a linear function that continuously increases without repeating any values.
- Thus, log(eωt) is not periodic.
- Both sin(ωt) and cos(ωt) are well-known periodic functions with a period of 2π.
- The sum of two periodic functions (with the same period) is also periodic.
- Therefore, sin(ωt)+cos(ωt) is periodic.
- Similar to the first function, e−ωt is also an exponential function.
- As t increases, e−ωt continuously decreases and does not return to any previous value.
- Hence, e−ωt is not periodic.
From the analysis, the only function that represents periodic motion is:
- sin(ωt)+cos(ωt)
Similar Questions
Knowledge Check
Which of the following x-t graphs does not represent periodic motion?
A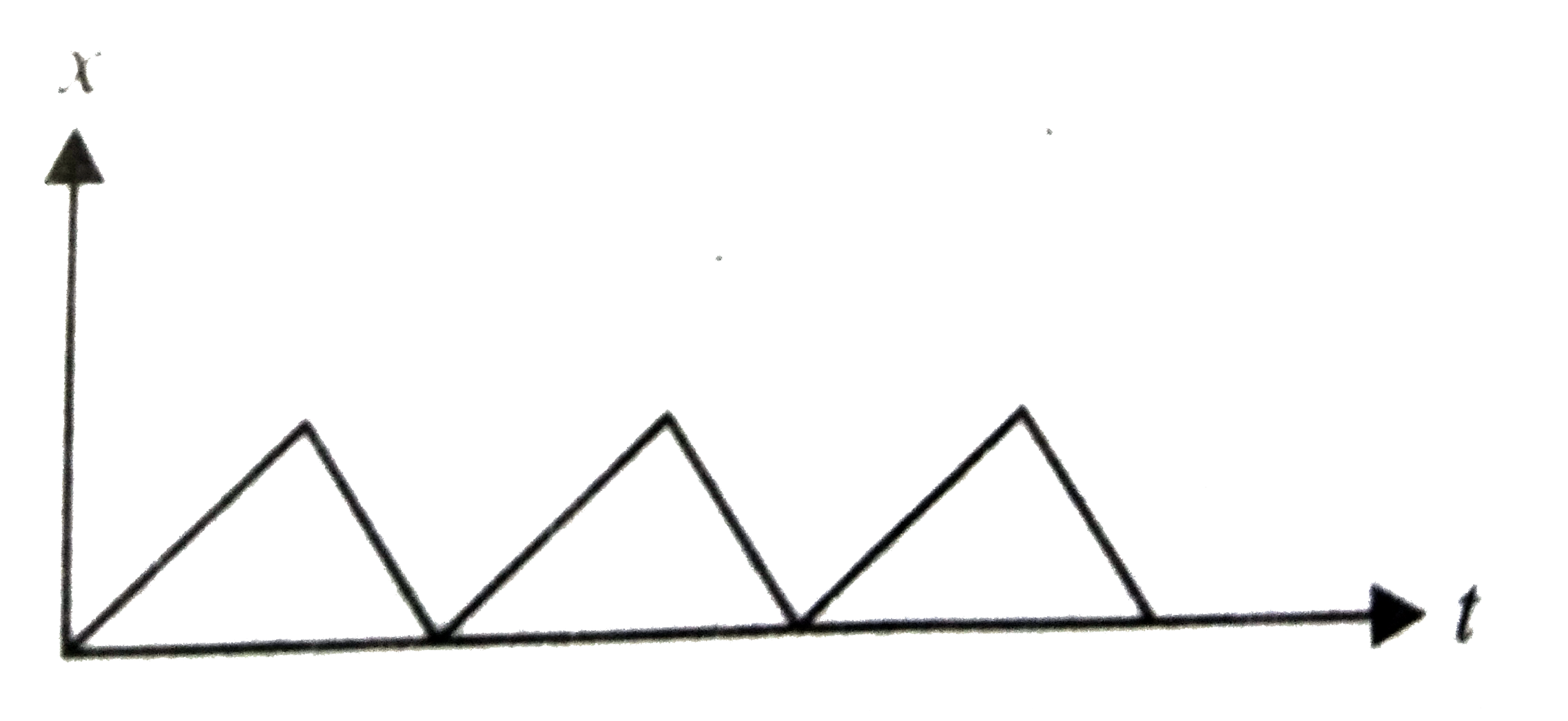 B
B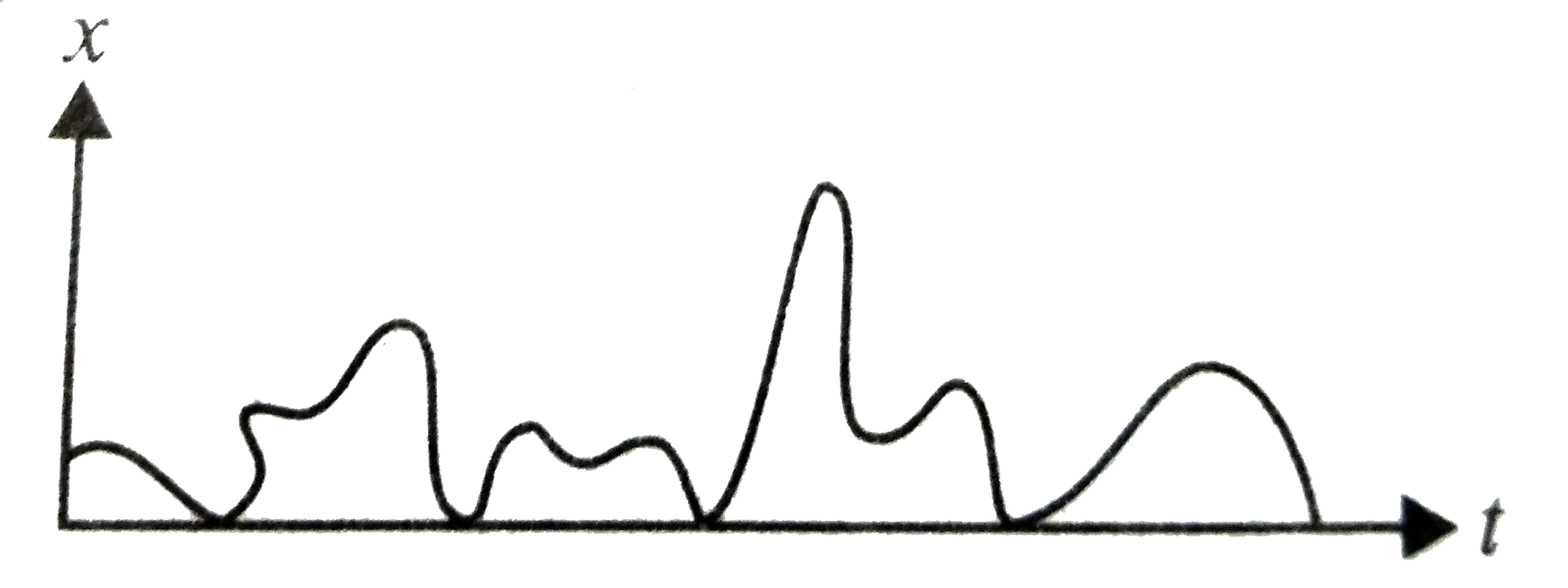 C
C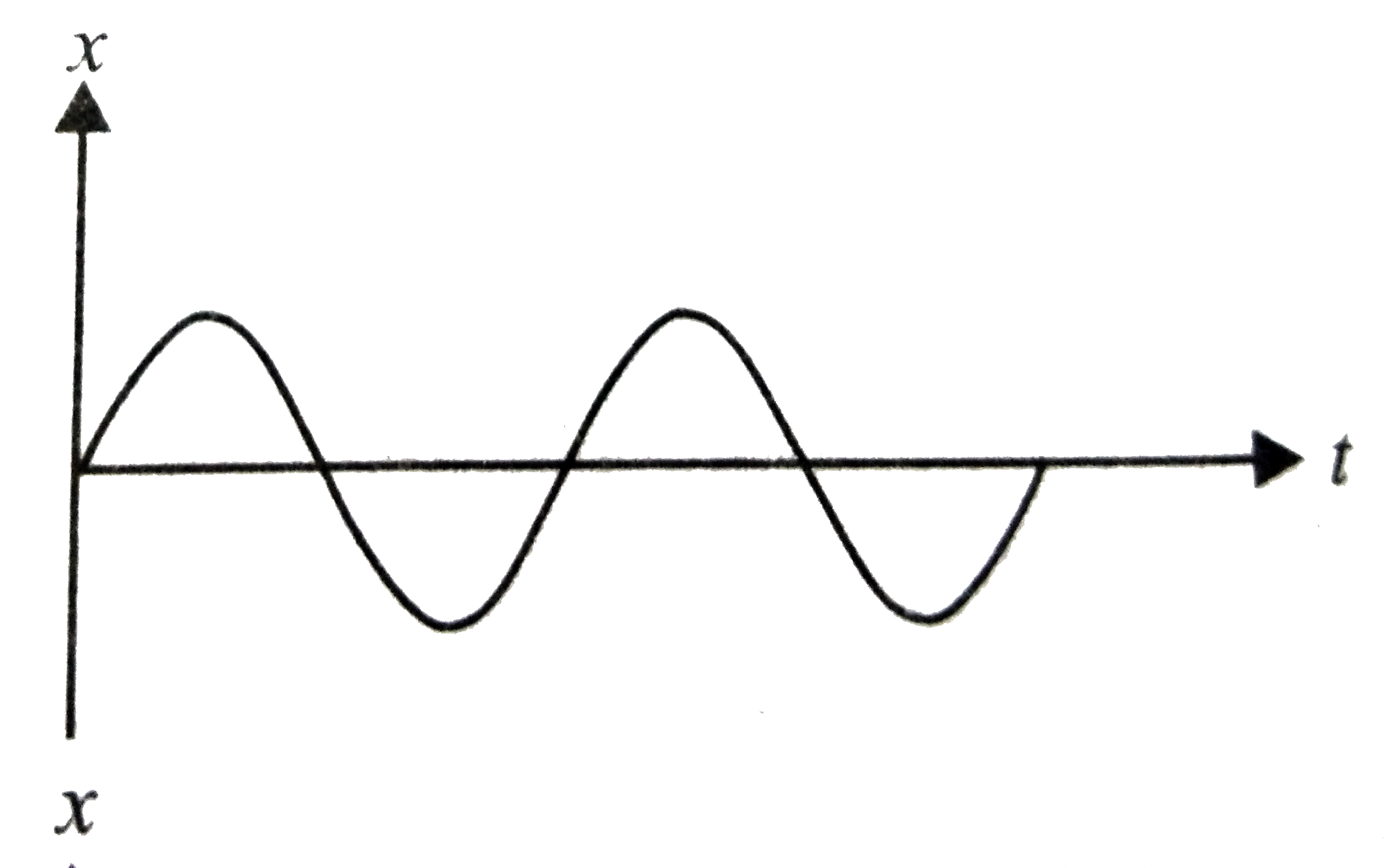 D
D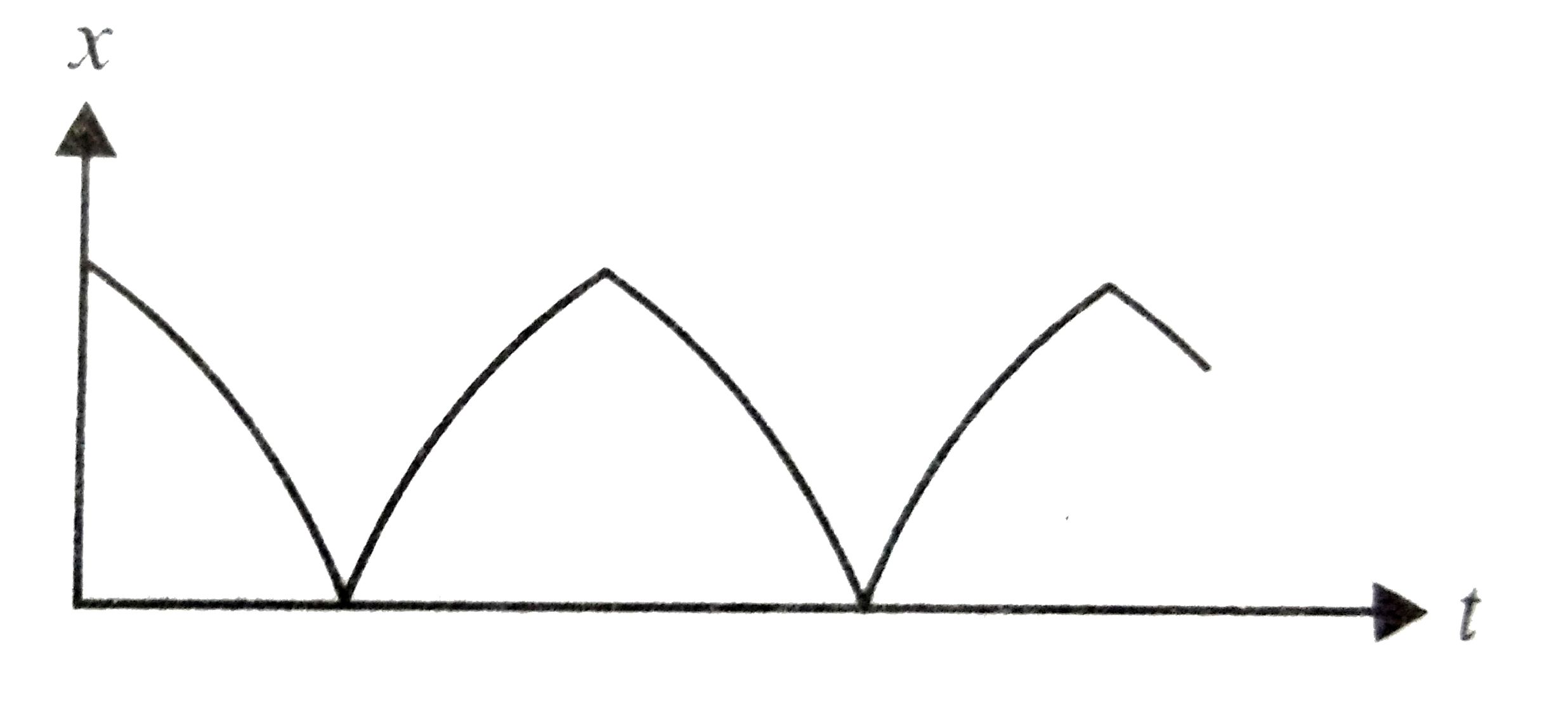
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) The rotation of earth about its axis. (b) Motion of an oscillating mercury column in a U tube,
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most position. (d) General vibrations of a polyatomic molecule about its equilibrium position.
View SolutionWhich of the following functions of time represented (a) periodic and (b) non-periodic motion ? Given the period for each case of periodic motion (ω is any positive constant(i)sinωt−cosωt(ii)log(2ω)
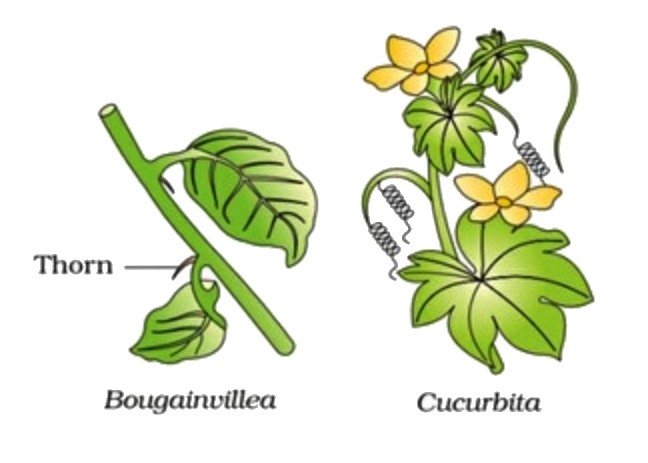
View SolutionIdentify the structure which represents homology in the following picture.
View SolutionFig. 14.23 depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion) ?

View SolutionDoes cosωt+sin2ωt+cos4ωt represent periodic motion ? If yes, then find the period(ω is any positive constant) .
Hint : ( Each term represents a periodic function with different angular freuency . Find the smallest interval of time after which the sum of three terms repeats ) .
View SolutionFor a particle executing simple harmonic motion, the displacement x is given by x=Acosωt. Identify the graph, which represents the variation of potential energy (U) as a function of time t and displacement x.

View SolutionWhich one of the following equations of motion represents simple harmonic motion ?
View Solution
