Which of the following functions of time represented (a) periodic and (b) non-periodic motion ? Given the period for each case of periodic motion (ω is any positive constant(i)sinωt−cosωt(ii)log(2ω)
To solve the question regarding periodic and non-periodic functions of time, we will analyze each function step by step.
Step 1: Analyze the first function y=sin(ωt)−cos(ωt)
1. Identify the nature of the function:
- Both sin(ωt) and cos(ωt) are periodic functions.
- The sine and cosine functions have a period of 2π.
2. Combine the functions:
- The function y=sin(ωt)−cos(ωt) can be expressed in a different form.
- We can rewrite it as:
y=√2(1√2sin(ωt)−1√2cos(ωt))
- This can be recognized as a sine function with a phase shift:
y=√2sin(ωt−π4)
3. Determine the period:
- The period T of the function sin(ωt) is given by:
T=2πω
Conclusion for the first function:
- Periodic: Yes
- Period: T=2πω
---
Step 2: Analyze the second function y=log(2ω)
1. Identify the nature of the function:
- The function log(2ω) is a logarithmic function.
- Logarithmic functions are not periodic; they continuously increase as ω increases.
2. Determine the period:
- Since the function is non-periodic, it does not have a defined period.
- We can state that the period is infinite.
Conclusion for the second function:
- Non-periodic: Yes
- Period: T=∞
---
Final Summary:
- Function (i): y=sin(ωt)−cos(ωt)
- Type: Periodic
- Period: T=2πω
- Function (ii): y=log(2ω)
- Type: Non-periodic
- Period: T=∞
---
- Both sin(ωt) and cos(ωt) are periodic functions.
- The sine and cosine functions have a period of 2π.
- The function y=sin(ωt)−cos(ωt) can be expressed in a different form.
- We can rewrite it as:
y=√2(1√2sin(ωt)−1√2cos(ωt))
- This can be recognized as a sine function with a phase shift:
y=√2sin(ωt−π4)
- The period T of the function sin(ωt) is given by:
T=2πω
- Periodic: Yes
- Period: T=2πω
- The function log(2ω) is a logarithmic function.
- Logarithmic functions are not periodic; they continuously increase as ω increases.
- Since the function is non-periodic, it does not have a defined period.
- We can state that the period is infinite.
- Non-periodic: Yes
- Period: T=∞
- Function (i): y=sin(ωt)−cos(ωt)
- Type: Periodic
- Period: T=2πω
- Type: Non-periodic
- Period: T=∞
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Try Yourself
86 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
Which of the following functions of time represent (a) simple harmonic (b) periodic but not simple harmonic and (c ) non periodic motion? Give period for each case of periodic motion (ω is nay positive constant)
(1) Sin3ωt (2) 3cos(π/4−2ωt)
(3) cosωt+cos3ωt+cos5ωt
(4) e−ω2t2 (5) 1+ωt+ω2t2
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωt
View Solution
Knowledge Check
Which of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωtAa simple harmonic motion with a period πω.Ba simple harmonic motion with a period 2πωCa periodic, but not simple harmonic motionn with a period πωDa periodic, but not simple harmonic motion with a period 2πωWhich of the following x-t graphs does not represent periodic motion?
A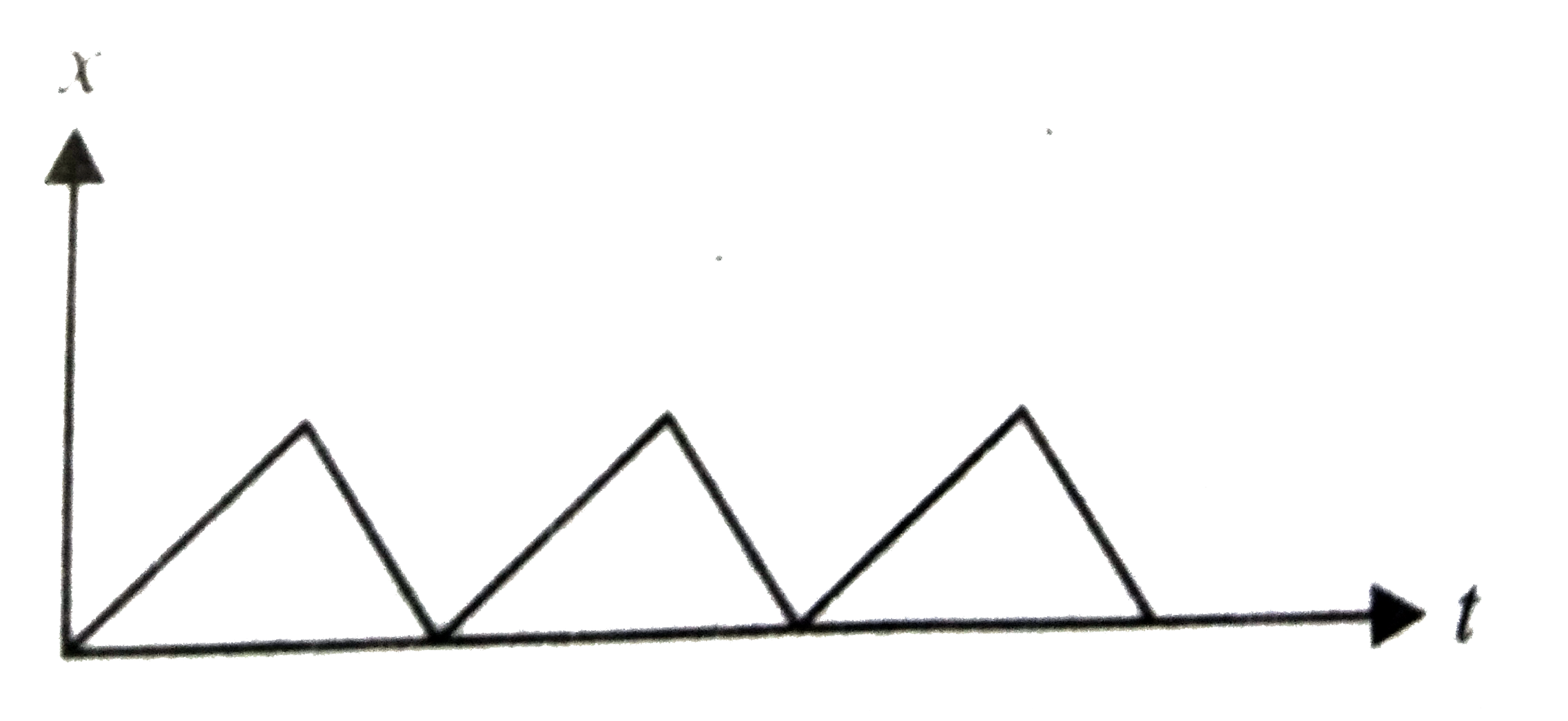 B
B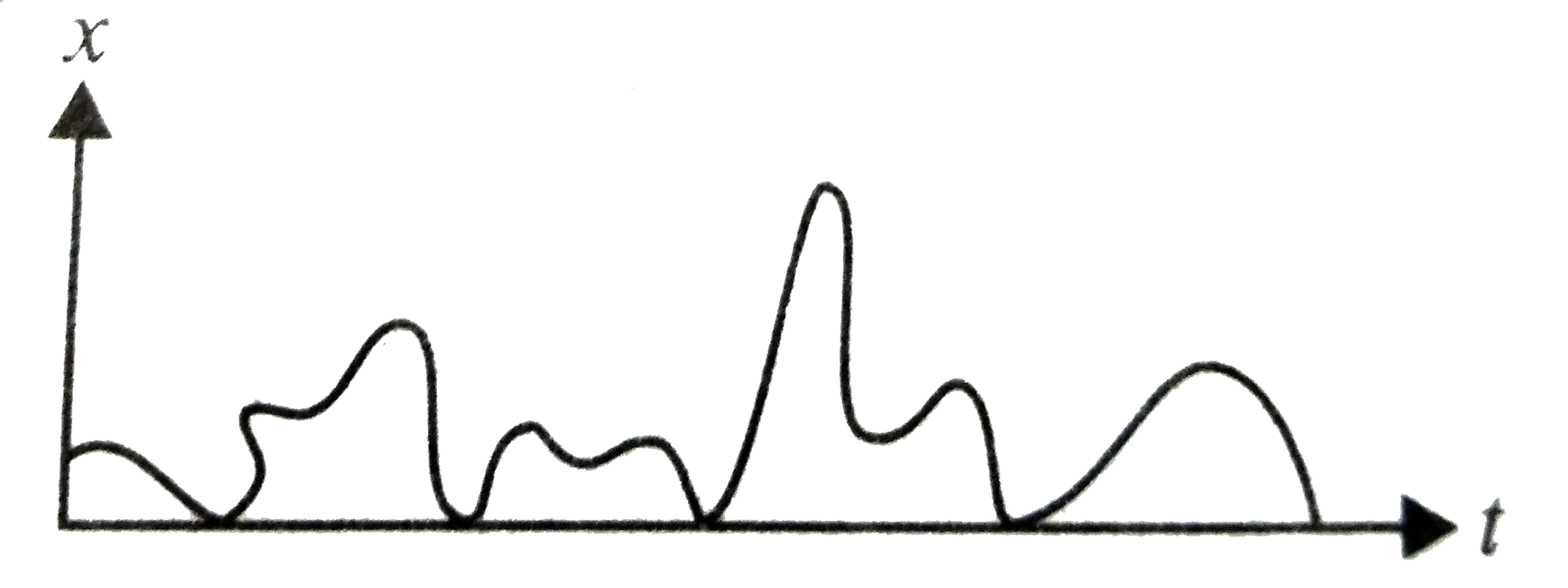 C
C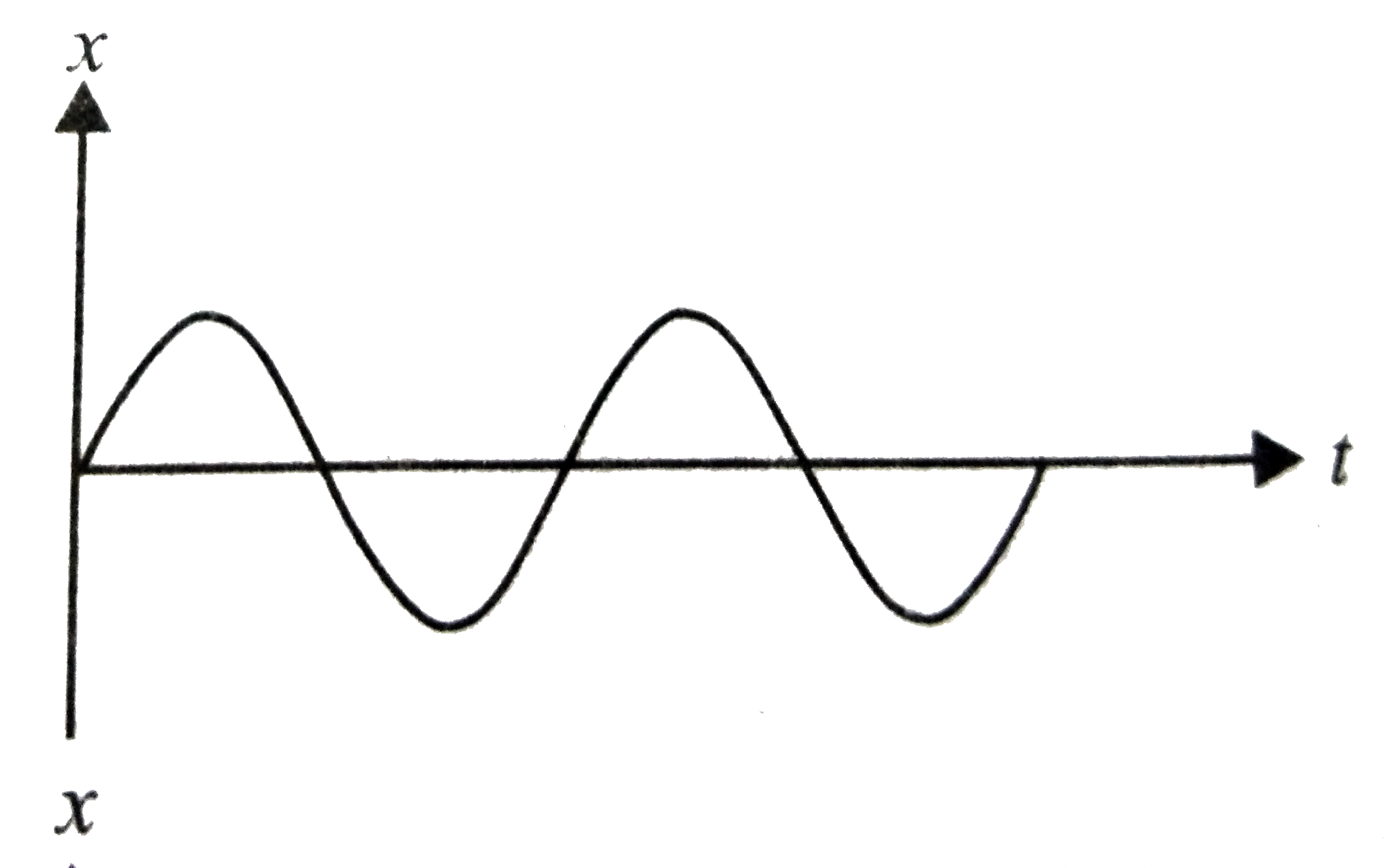 D
D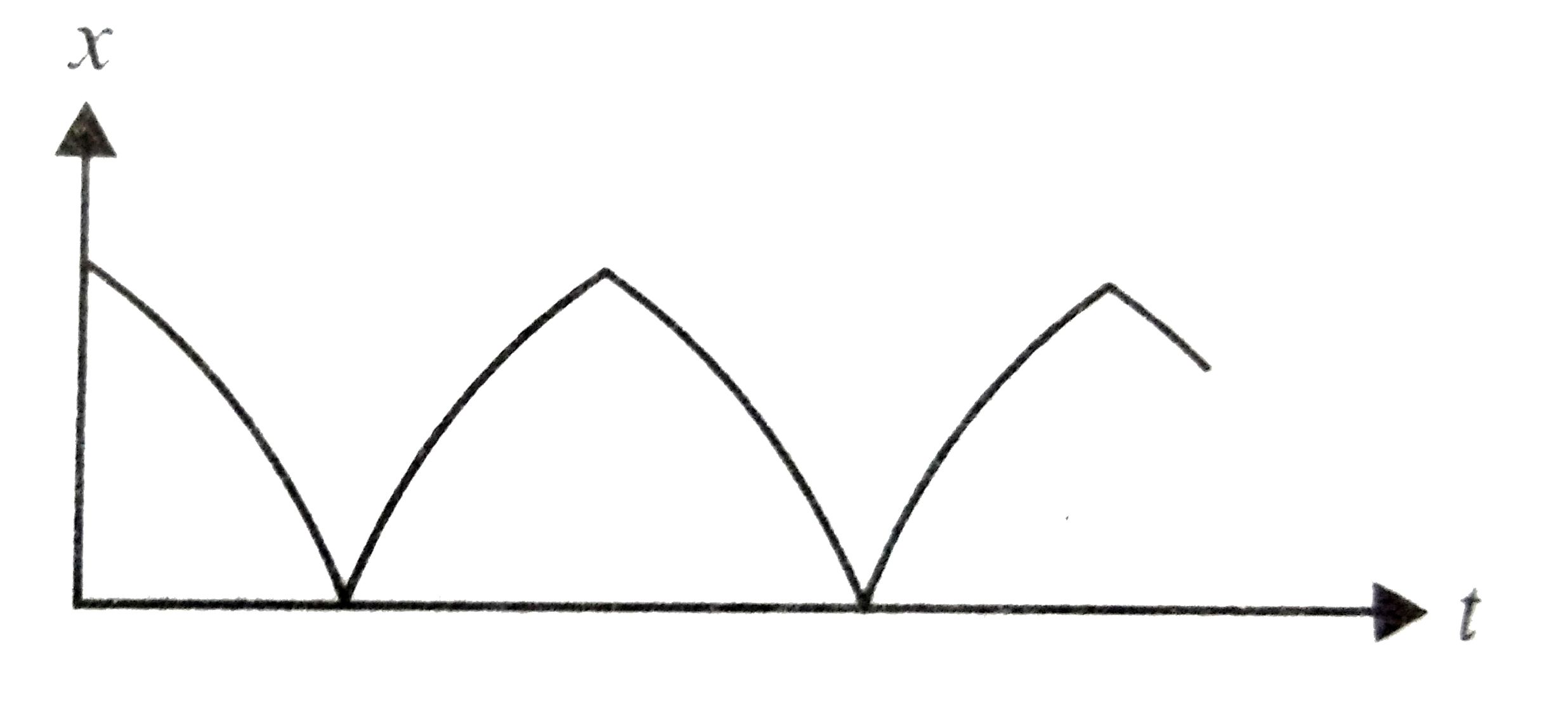
Identify function which represent periodic motion
View SolutionWhich of the following is correctly matched w.r.t. era and its period?
View SolutionDoes eωt represent periodic motion ? Ifyes, then find the period (ω is any positive constant )
Hint : (Think , Does it repeat itself)
View SolutionCategorise the following function of time eω2t as
(a) S.H.M.
(b) Periodic but not S.H.M. Also , give period if it is periodic motion.
Hint : Doest it repeat itself ?
View SolutionCategories the following function of time 3sin(2ωt−π4) as
(a) SHM , (b) Periodic but not SHM. Also give the period.
View SolutionWhich of the following functions represent SHM :-
(i) sin2ωt , (ii) sinωt+2cosωt , (iii) sinωt+cos2ωt
View Solution
