Does cosωt+sin2ωt+cos4ωt represent periodic motion ? If yes, then find the period(ω is any positive constant) .
Hint : ( Each term represents a periodic function with different angular freuency . Find the smallest interval of time after which the sum of three terms repeats ) .
To determine if the function y=cos(ωt)+sin(2ωt)+cos(4ωt) represents periodic motion, we need to analyze the periodicity of each term and find the overall period of the sum.
1. Identify the Periods of Each Term:
- The period of cos(ωt):
T1=2πω
- The period of sin(2ωt):
T2=2π2ω=πω
- The period of cos(4ωt):
T3=2π4ω=π2ω
2. Find the Least Common Multiple (LCM):
- We need to find the LCM of the three periods T1,T2,T3:
- T1=2πω
- T2=πω
- T3=π2ω
- To find the LCM, we express the periods with a common denominator:
- T1=2πω=4π2ω
- T2=πω=2π2ω
- T3=π2ω
- Now, we have:
- T1=4π2ω
- T2=2π2ω
- T3=π2ω
- The LCM of 4π2ω,2π2ω,π2ω is 4π2ω since it is the largest of the three.
3. Conclusion:
- The overall period T of the function y is:
T=4π2ω=2πω
Thus, the function y=cos(ωt)+sin(2ωt)+cos(4ωt) does represent periodic motion, and the period is 2πω.
- The period of cos(ωt):
T1=2πω
- The period of sin(2ωt):
T2=2π2ω=πω
- The period of cos(4ωt):
T3=2π4ω=π2ω
- We need to find the LCM of the three periods T1,T2,T3:
- T1=2πω
- T2=πω
- T3=π2ω
- T1=2πω=4π2ω
- T2=πω=2π2ω
- T3=π2ω
- T1=4π2ω
- T2=2π2ω
- T3=π2ω
- The overall period T of the function y is:
T=4π2ω=2πω
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)58videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )25videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)13videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
Similar Questions
Does eωt represent periodic motion ? Ifyes, then find the period (ω is any positive constant )
Hint : (Think , Does it repeat itself)View SolutionCategorise the following function of time :sinωt+sin3ωt+sin5ωt as
(a) S.H.M.
(b) Periodic but no S.H.M. .Also give the period.
Hint : Find the smallest interval of time after which the sum of 3 terms repeatsView SolutionCategorise the following function of time :sinωt+sin5ωt as
(a) S.H.M.
(b) Periodic but no S.H.M. .Also give the period.
Hint : Find the smallest interval of time after which the sum of 2 terms repeatsView SolutionWhich of the following functions of time represented (a) periodic and (b) non-periodic motion ? Given the period for each case of periodic motion (ω is any positive constant(i)sinωt−cosωt(ii)log(2ω)
View SolutionEquations y1=Asinωtandy2=A2sinωt+A2cosωtrepresent S.H.M. The ratio of the amplitudes of the two motions is
View SolutionThe function x=Asin2(ω)t+Bcos2(ω)t+Csin(ω)tcos(ω)t represent (SHM) for which of the option(s).
View SolutionA point moves in the plane xy according to the law x=asinωt, y=a(1−cosωt), where a and ω are positive constants. Find:
(a) the distance s traversed by the point during the time τ,
View SolutionTwo particles P1 and P2 are performing SHM along the same line about the same mean position , initial they are at their extreme position. If the time period of each particle is 12 sec and the difference of their amplitude is 12cm then find the minimum time after which the separation between the particle becomes 6cm.
View SolutionFind time period of the function, y=sinωt+sin2ωt+sin3ωt
View SolutionFrom the given graph , find time period and frequency for A and B.
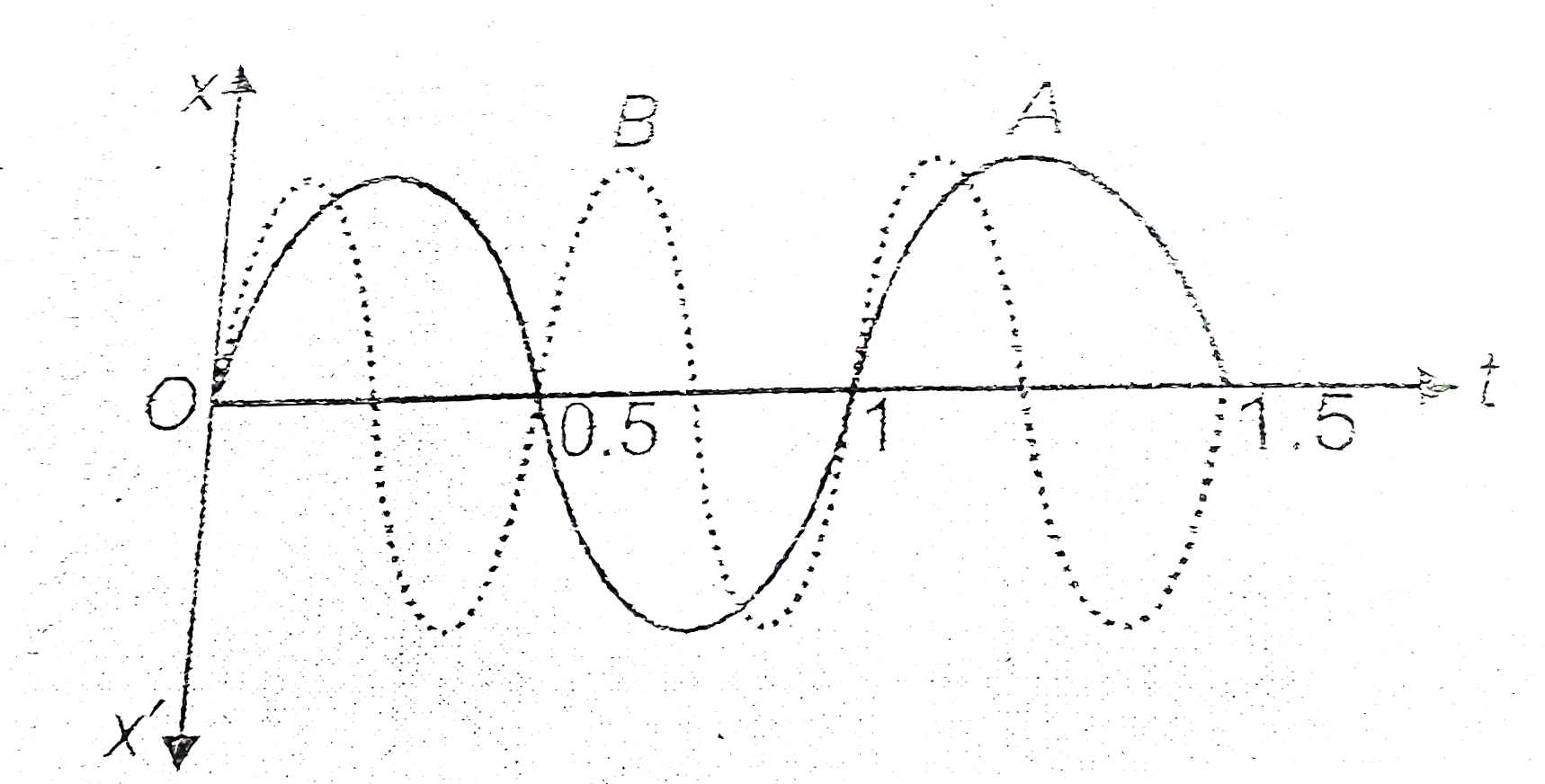
Hint : Find the time after which the motion is repeated . This gives time period T. Frequency v=1T0View Solution

