If ABCDEF is a regular hexagon, prove that .
To prove that →AD+→EB+→FC=4→AB for a regular hexagon ABCDEF, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon can be inscribed in a circle, and all its sides are equal. Let the length of each side be AB=a. The vertices of the hexagon can be represented in a coordinate system.
Step 2: Assign Coordinates to the Vertices
We can assign coordinates to the vertices of the hexagon as follows:
- A(1,0)
- B(12,√32)
- C(−12,√32)
- D(−1,0)
- E(−12,−√32)
- F(12,−√32)
Step 3: Express the Vectors
Now we express the vectors →AD, →EB, and →FC:
- →AD=→D−→A=(−1,0)−(1,0)=(−2,0)
- →EB=→B−→E=(12,√32)−(−12,−√32)=(1,√3)
- →FC=→C−→F=(−12,√32)−(12,−√32)=(−1,√3)
Step 4: Add the Vectors
Now we add these vectors:
→AD+→EB+→FC=(−2,0)+(1,√3)+(−1,√3)
Calculating the components:
- For the x-component: −2+1−1=−2
- For the y-component: 0+√3+√3=2√3
Thus, we have:
→AD+→EB+→FC=(−2,2√3)
Step 5: Calculate 4→AB
Now, we calculate 4→AB:
→AB=→B−→A=(12,√32)−(1,0)=(−12,√32)
Thus,
4→AB=4(−12,√32)=(−2,2√3)
Step 6: Conclusion
Since both sides are equal:
→AD+→EB+→FC=4→AB
This proves that →AD+→EB+→FC=4→AB.
---
A regular hexagon can be inscribed in a circle, and all its sides are equal. Let the length of each side be AB=a. The vertices of the hexagon can be represented in a coordinate system.
We can assign coordinates to the vertices of the hexagon as follows:
- A(1,0)
- B(12,√32)
- C(−12,√32)
- D(−1,0)
- E(−12,−√32)
- F(12,−√32)
Now we express the vectors →AD, →EB, and →FC:
- →AD=→D−→A=(−1,0)−(1,0)=(−2,0)
- →EB=→B−→E=(12,√32)−(−12,−√32)=(1,√3)
- →FC=→C−→F=(−12,√32)−(12,−√32)=(−1,√3)
Now we add these vectors:
→AD+→EB+→FC=(−2,0)+(1,√3)+(−1,√3)
Calculating the components:
- For the x-component: −2+1−1=−2
- For the y-component: 0+√3+√3=2√3
→AD+→EB+→FC=(−2,2√3)
Now, we calculate 4→AB:
→AB=→B−→A=(12,√32)−(1,0)=(−12,√32)
Thus,
4→AB=4(−12,√32)=(−2,2√3)
Since both sides are equal:
→AD+→EB+→FC=4→AB
This proves that →AD+→EB+→FC=4→AB.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
If ABCDEF is a regular hexagon, prove that −−→AC+−−→AD+−−→EA+−−→FA=3−−→AB
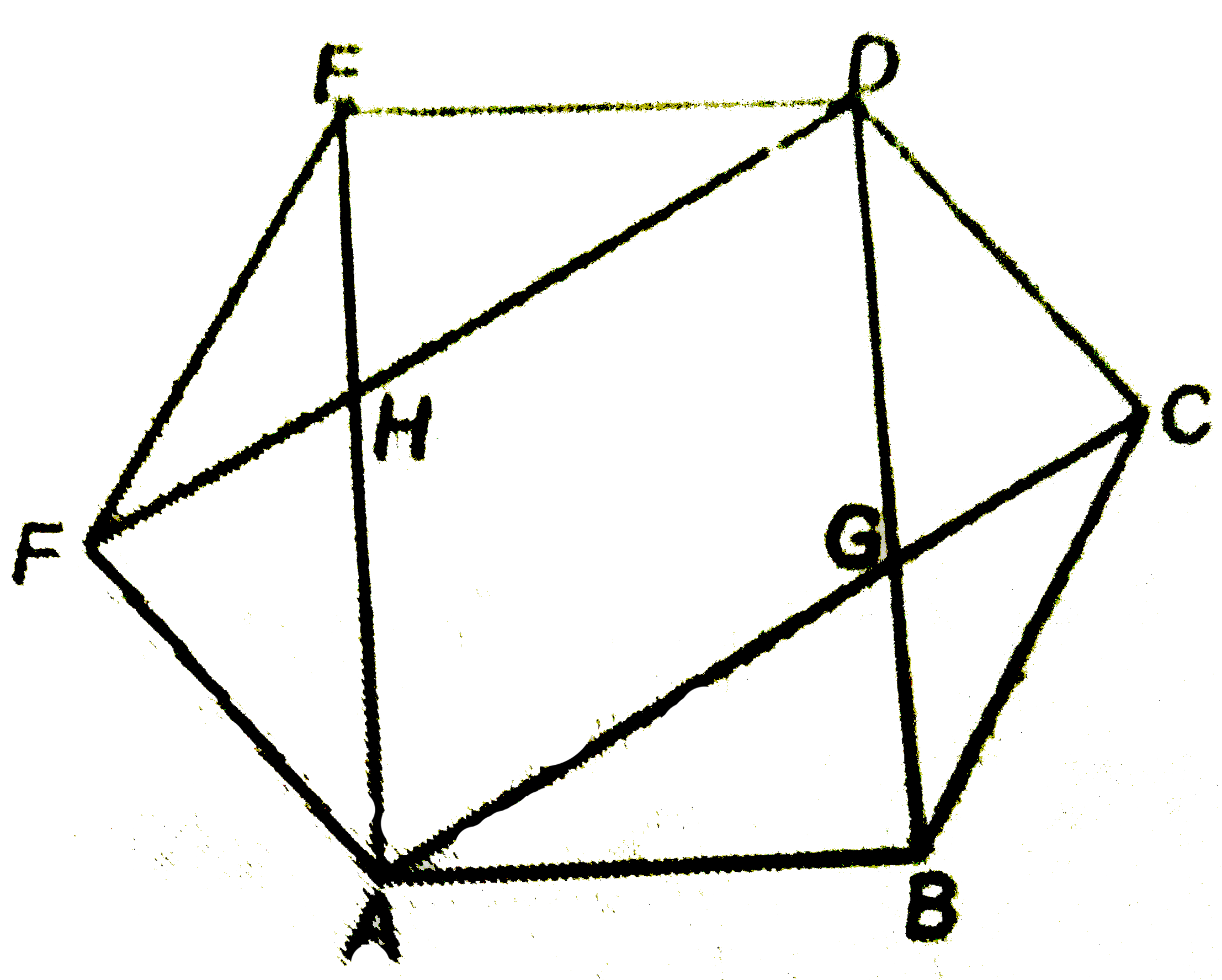
View SolutionIn the adjoining figure, ABCDEF is a regular hexagon. Prove that □ABDE,□ACDFand□AGDH are parallelograms.
View SolutionConsider the regular hexagon ABCDEF with centre at O (origin).
Q. AD+EB+FC is equal to
View SolutionIf ABCDEF is a regular hexagon then −−→AD+−−→EB+−−→FC equals :
View SolutionIf ABCDEF is a regualr hexagon, then −−→AC+−−→AD+−−→EA+−−→FA=
View SolutionIf ABCDEF is a regular hexagon with −−→AB=→a and −−→BC=→b, then −−→CE equals
View SolutionABCDEF is a regular hexagon , with the sides AB, AC, AD, AE and AF representing vectors 1 unit , 2 units , 3 units , 4 units and 5 units respetively . Find their resultant ?
View SolutionABCDEF is a regular hexagon of side a. At each vertex A,B and C a point charge +q is fixed and D,E,F a point charge −q is fixed. Intensity of electric field at a point lying on the line joining FC at a distance x away from the centre of hexagon (x>>>>a) is found to be √αaq2πε0x3 where α is an integer. Find α
View SolutionIn a regular hexagon ABCDEF, −−→AE
View SolutionIn the given figure, ABCDEF is a regular hexagon, which vectors are:
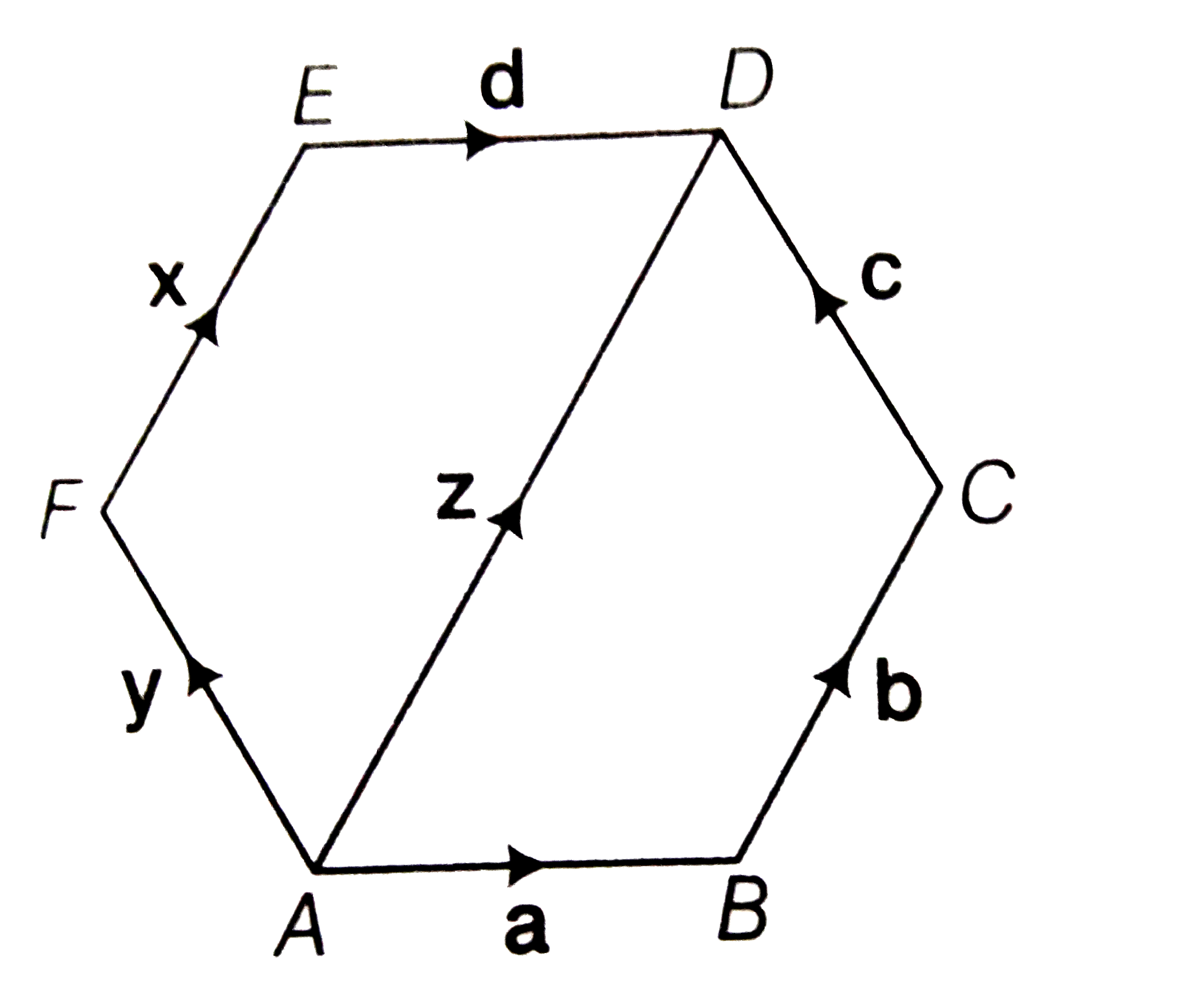
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
View Solution
