Match the following Column I to Column II

(A) 4a2+9b2+16c2=2(3ab+6bc+4ca)
(2a)2+(3b)2+(4c)2−(2a)(3b)(4c)−(2a)(4c)=0
12{(2a−3b)2+(3b−4c)2+(4c−2a)2}=0
⇒2a−3b=0 and 3b−4c=0
and 4c−2a=0⇒2a=3b
and 3b=4c and 4c=2a
⇒a=32b and b=43c and c=12a
⇒a=32b and b=43c and c=34b
So, a,b,c are 32b,b,34b
Reciprocal of the terms 23b,1b,43b.
which is in AP.
So, these a,b,c are in HP.
(B) 17a2+13b2+5c2=3ab+15bc+5ca
⇒34a2+26b2+10c2−6ab−30bc−10ca=0
⇒(3a−b)2+(5b−3c)2+(c−5a)2=0
⇒3a−b=0 and 5b−3c=0 and c−5a=0
⇒a1=b3=c5=λ [ say ]
∴a=λ,b=3λ,c=5λ
Hence, a,b,c are in AP.
(C ) a2+9b2+25c2=abc(15a+5b+3c)
(a)2+(3b)2+(5c)2−15bc−5ac−3ab=0
12{(a−3b)2+(3b−5c)2+(5c−a)2}=0
⇒a−3b=0 and 3b−5c=0 and 5c−a=0
⇒a=3b and 3b=5c and 5c=a
⇒a=3b and b=53c and c=a5
⇒a=3b and b=53c and c=35b
So, a,b,c are of the form 3b,b,3b5.
Reciprocal of 3b,b,3b5 are 13b,1b,53b, which are in AP.
[∴1b−13b=23b annd 53b−1b=23b]
(D) (a2+b2+c2)p2−2p(qb+bc+ca)+a2+b2+c2≤0
⇒(a2p2+b2−2abp)+(b2p2+c2−2pbc)+(c2p2+a2−2acp)≤0
⇒(ap−b)2+(bp−c)2+(cp−a)2≤0
⇒(ap−b)2+(bp−c)2+(cp−a)2=0
⇒ap−b=0 and bp−c=0 and cp−a=0
⇒p=ba and p=cb and p=ac
⇒ba=cb=ac
implies a,b,c are in GP.
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Matching Type Questions1videos
SEQUENCES AND SERIES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Statement I And Ii Type Questions)7videos
SEQUENCES AND SERIES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Single Integer Answer Type Questions)10videos
SEQUENCES AND SERIES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)12videos
SETS, RELATIONS AND FUNCTIONS
Similar Questions
Match the following Column I with Column II
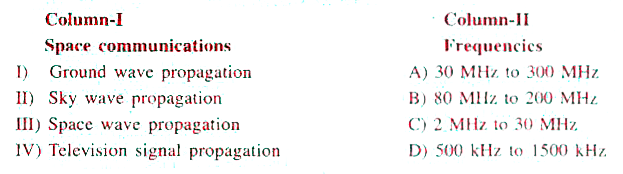
CodeView SolutionMatch the following Column I Column II A. Rhizopus 1. Ascomycetes B. Penicllium 2. Basidiomycetes C. Ustilago 3. Deuteromycetes D. Alternaria 4. Phycomycetes
View SolutionMatch the following (Column I with Column II).
 View Solution
View SolutionMatch the following Column I with column II:
 View Solution
View SolutionMatch the following (Column I with Column II)
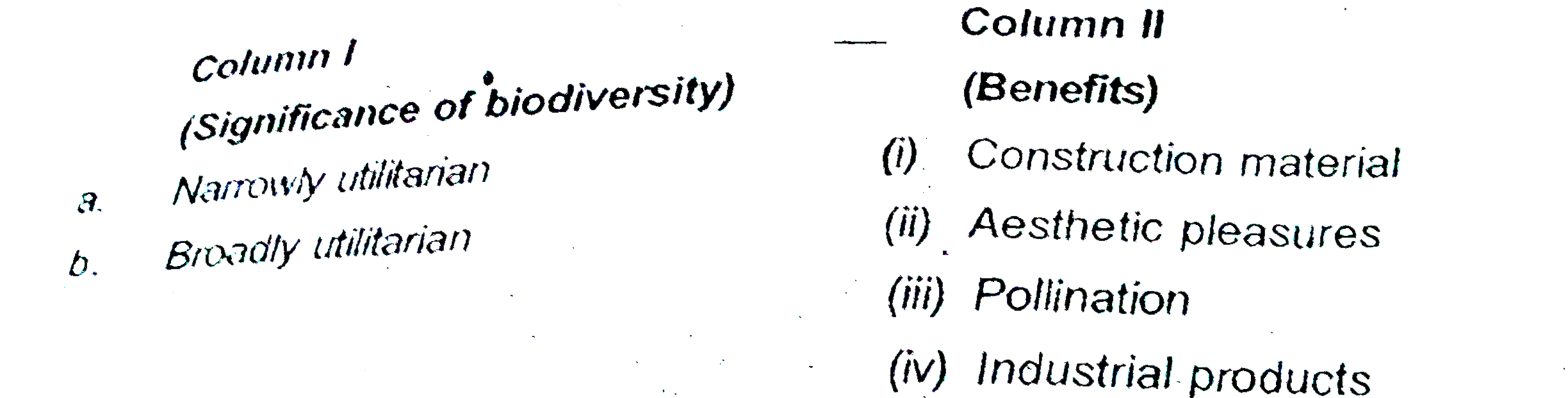 View Solution
View SolutionMatch the following (Column -I and Column II)
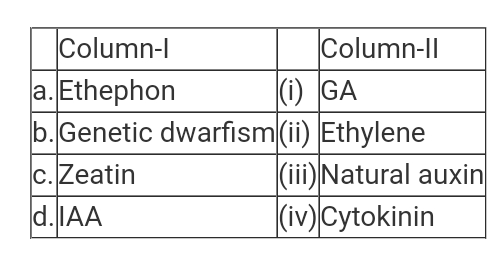 View Solution
View SolutionMatch the following column I with column II :
 View Solution
View SolutionMatch the following column I with column II and choose the option with the accurate matches.
 View Solution
View SolutionMatch the following column I with column II and choose the correct combination.
ColumnIColumnII(a)Earthworm(i)Gizzard(b)Cockroach(ii)Caecum(c)Frog(iii)Clitellum(d)Rat(iv)CloacaView SolutionA block of mass m is thrown upwards with some initial velocity up a rough inclined plane as shown

Match the following Column-I with Column-II
 View Solution
View Solution

