Find the cartesian coordinates of the points whose polar coordinates are
(5,π−tan−1(43))
The correct Answer is:(-3, 4)
To find the Cartesian coordinates of the point whose polar coordinates are given as (5,π−tan−1(43)), we will follow these steps:
Step 1: Identify the values of r and θ
From the polar coordinates, we have:
- r=5
- θ=π−tan−1(43)
Step 2: Calculate tan(θ)
Using the identity for tangent, we have:
tan(θ)=tan(π−tan−1(43))=−tan(tan−1(43))=−43
This means that:
cot(θ)=−34
Step 3: Determine the sides of the right triangle
From the cotangent value, we can identify the sides of the right triangle:
- Base (adjacent side) = -4 (since cotangent is negative in the second quadrant)
- Perpendicular (opposite side) = 3
Step 4: Calculate the hypotenuse
Using the Pythagorean theorem:
Hypotenuse=√(−4)2+32=√16+9=√25=5
Step 5: Calculate cos(θ) and sin(θ)
Now, we can find cos(θ) and sin(θ):
cos(θ)=BaseHypotenuse=−45
sin(θ)=PerpendicularHypotenuse=35
Step 6: Convert to Cartesian coordinates
Using the formulas:
x=rcos(θ)andy=rsin(θ)
Substituting the values:
x=5⋅(−45)=−4
y=5⋅(35)=3
Step 7: Write the final Cartesian coordinates
Thus, the Cartesian coordinates are:
(−4,3)
From the polar coordinates, we have:
- r=5
- θ=π−tan−1(43)
Using the identity for tangent, we have:
tan(θ)=tan(π−tan−1(43))=−tan(tan−1(43))=−43
This means that:
cot(θ)=−34
From the cotangent value, we can identify the sides of the right triangle:
- Base (adjacent side) = -4 (since cotangent is negative in the second quadrant)
- Perpendicular (opposite side) = 3
Using the Pythagorean theorem:
Hypotenuse=√(−4)2+32=√16+9=√25=5
Now, we can find cos(θ) and sin(θ):
cos(θ)=BaseHypotenuse=−45
sin(θ)=PerpendicularHypotenuse=35
Using the formulas:
x=rcos(θ)andy=rsin(θ)
Substituting the values:
x=5⋅(−45)=−4
y=5⋅(35)=3
Thus, the Cartesian coordinates are:
(−4,3)
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
The cartesian coordinates of the point whose polar coordinates are (13,π−tan−1(512)) is
View SolutionFind the Cartesian co-ordinates of point whose polar co-ordinates are (4,π3).
View SolutionFind the polar coordinates of the points whose cartesian coordinates are
(−3,4)
View SolutionFind the polar coordinates of the points whose cartesian coordinates are
(−2,−2)
View SolutionThe polar coordinates of the point whose cartesian coordinates are (-1, -1) is
View SolutionThe cartesian coordinates of the point Q in the figure is
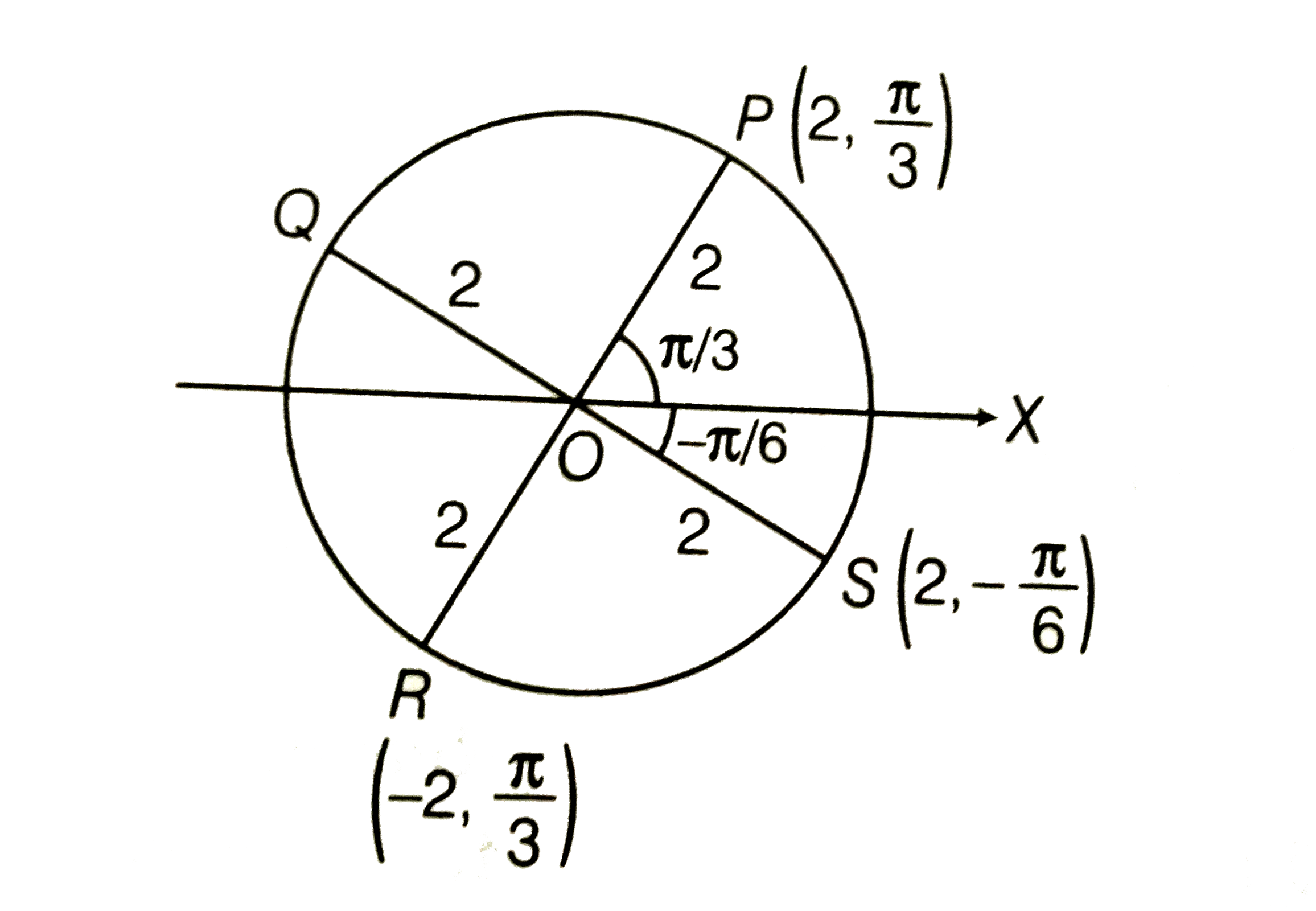
View SolutionThe Cartesian coordinates of point having polar coordinates(−2,2π3)will be
View SolutionConvert the following Cartesian coordinates to the cooresponding polar coordinates using positive r.
(i) (1,−1)
(ii) (−3,−4)
View SolutionFind the coor dinates of the centrod of a triangle whose coordinates are (3, -5, 7), (-1, 7, -6)
and (1, 1, 2).
View SolutionFind the distances of the point P(−4,3,5) from the coordinate axes.
View Solution
