The cartesian coordinates of the point whose polar coordinates are (13,π−tan−1(512)) is
(12, 5)
(-12, 5)
(-12, -5)
(12, -5)
The correct Answer is:B
To convert the polar coordinates (13,π−tan−1(512)) into Cartesian coordinates, we will follow these steps:
Step 1: Identify the polar coordinates
The polar coordinates are given as:
- r=13
- θ=π−tan−1(512)
Step 2: Determine the Cartesian coordinates formula
The Cartesian coordinates (x,y) can be found using the formulas:
- x=rcos(θ)
- y=rsin(θ)
Step 3: Analyze the angle θ
Since θ=π−tan−1(512), we need to understand the position of this angle:
- The angle tan−1(512) is in the first quadrant, which means that π−tan−1(512) is in the second quadrant.
- In the second quadrant, the cosine value is negative and the sine value is positive.
Step 4: Calculate cos(θ) and sin(θ)
Using the right triangle formed by the opposite side (perpendicular) and adjacent side (base):
- Opposite side = 5
- Adjacent side = 12
- Hypotenuse can be calculated using Pythagorean theorem:
Hypotenuse=√52+122=√25+144=√169=13
Now we can find:
- cos(θ)=−AdjacentHypotenuse=−1213
- sin(θ)=OppositeHypotenuse=513
Step 5: Substitute values into the Cartesian formulas
Now substituting the values of r, cos(θ), and sin(θ) into the Cartesian formulas:
- For x:
x=rcos(θ)=13⋅(−1213)=−12
- For y:
y=rsin(θ)=13⋅513=5
Step 6: Write the final Cartesian coordinates
Thus, the Cartesian coordinates are:
(x,y)=(−12,5)
Final Answer
The Cartesian coordinates of the point whose polar coordinates are (13,π−tan−1(512)) is (−12,5).
---
The polar coordinates are given as:
- r=13
- θ=π−tan−1(512)
The Cartesian coordinates (x,y) can be found using the formulas:
- x=rcos(θ)
- y=rsin(θ)
Since θ=π−tan−1(512), we need to understand the position of this angle:
- The angle tan−1(512) is in the first quadrant, which means that π−tan−1(512) is in the second quadrant.
- In the second quadrant, the cosine value is negative and the sine value is positive.
Using the right triangle formed by the opposite side (perpendicular) and adjacent side (base):
- Opposite side = 5
- Adjacent side = 12
- Hypotenuse can be calculated using Pythagorean theorem:
Hypotenuse=√52+122=√25+144=√169=13
- cos(θ)=−AdjacentHypotenuse=−1213
- sin(θ)=OppositeHypotenuse=513
Now substituting the values of r, cos(θ), and sin(θ) into the Cartesian formulas:
- For x:
x=rcos(θ)=13⋅(−1213)=−12
- For y:
y=rsin(θ)=13⋅513=5
Thus, the Cartesian coordinates are:
(x,y)=(−12,5)
The Cartesian coordinates of the point whose polar coordinates are (13,π−tan−1(512)) is (−12,5).
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 3
19 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
The equation of the perpendicular bisector of the segment joining the points whose coordinates are (1,4) and (-2,3) is
A3x−2y+5=0Bx−3y+2=0C3x+y−2=0Dx=3y+11=0
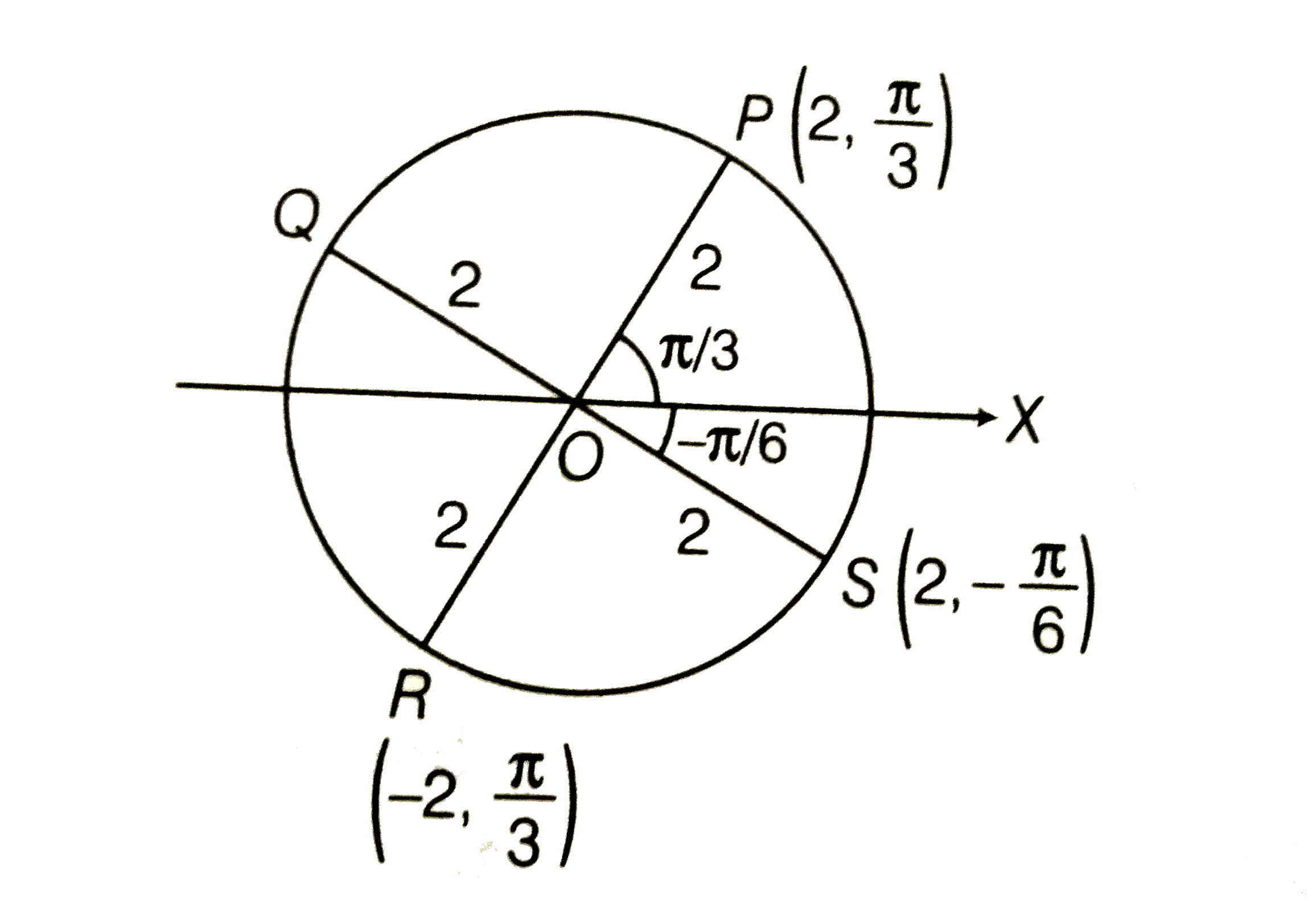
The cartesian coordinates of the point Q in the figure is
View SolutionFind the Cartesian co-ordinates of point whose polar co-ordinates are (4,π3).
View SolutionFind the polar coordinates of the points whose cartesian coordinates are
(−3,4)
View SolutionThe Cartesian coordinates of point having polar coordinates(−2,2π3)will be
View SolutionFind the polar coordinates of the points whose cartesian coordinates are
(−2,−2)
View SolutionConvert the following Cartesian coordinates to the cooresponding polar coordinates using positive r.
(i) (1,−1)
(ii) (−3,−4)
View SolutionWrite the coordinates of the points marked on the axes in Fig. 3.12.
View Solution
