The line segment joining to is doubled in length by having its length added to each end , then the ordinates of new ends are
The correct Answer is:
To solve the problem of finding the ordinates of the new ends of the line segment joining points A(6, 3) and B(-1, -4) after doubling its length, we can follow these steps:
Step 1: Calculate the Length of the Original Line Segment
The length of the line segment AB can be calculated using the distance formula:
Length=√(x2−x1)2+(y2−y1)2
Here, A(6,3) and B(−1,−4):
Length=√((−1)−6)2+((−4)−3)2=√(−7)2+(−7)2=√49+49=√98=7√2
Step 2: Determine the New Length After Doubling
Since we need to double the length of the segment, we multiply the original length by 2:
New Length=2×7√2=14√2
Step 3: Find the Midpoint of the Original Segment
The midpoint M of segment AB can be found using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
M=(6+(−1)2,3+(−4)2)=(52,−12)
Step 4: Calculate the Direction Vector from A to B
The direction vector →d from A to B is given by:
→d=(x2−x1,y2−y1)=(−1−6,−4−3)=(−7,−7)
Step 5: Normalize the Direction Vector
To normalize the direction vector, we divide by its length:
Length of →d=√(−7)2+(−7)2=7√2
The unit vector ^d is:
^d=(−1,−1) (normalized direction vector)
Step 6: Calculate the New Endpoints
To find the new endpoints, we need to move from the midpoint M in both directions along the direction vector scaled by half the new length:
New Length from Midpoint=14√22=7√2
The new coordinates of the endpoints can be calculated as:
1. New point C:
C=M+7√2⋅^d=(52−7,−12−7)=(52−142,−12−142)=(−92,−152)
2. New point D:
D=M−7√2⋅^d=(52+7,−12+7)=(52+142,−12+142)=(192,132)
Step 7: Identify the Ordinates
The ordinates of the new endpoints C and D are:
- For point C: y=−152
- For point D: y=132
Final Answer
The ordinates of the new ends are:
132 and −152
The length of the line segment AB can be calculated using the distance formula:
Length=√(x2−x1)2+(y2−y1)2
Here, A(6,3) and B(−1,−4):
Length=√((−1)−6)2+((−4)−3)2=√(−7)2+(−7)2=√49+49=√98=7√2
Since we need to double the length of the segment, we multiply the original length by 2:
New Length=2×7√2=14√2
The midpoint M of segment AB can be found using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
M=(6+(−1)2,3+(−4)2)=(52,−12)
The direction vector →d from A to B is given by:
→d=(x2−x1,y2−y1)=(−1−6,−4−3)=(−7,−7)
To normalize the direction vector, we divide by its length:
Length of →d=√(−7)2+(−7)2=7√2
The unit vector ^d is:
^d=(−1,−1) (normalized direction vector)
To find the new endpoints, we need to move from the midpoint M in both directions along the direction vector scaled by half the new length:
New Length from Midpoint=14√22=7√2
The new coordinates of the endpoints can be calculated as:
1. New point C:
C=M+7√2⋅^d=(52−7,−12−7)=(52−142,−12−142)=(−92,−152)
2. New point D:
D=M−7√2⋅^d=(52+7,−12+7)=(52+142,−12+142)=(192,132)
The ordinates of the new endpoints C and D are:
- For point C: y=−152
- For point D: y=132
The ordinates of the new ends are:
132 and −152
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
The line segment joining A(2,3)andB(−3,5) is extended through each end by a length equal to its original length. Find the coordinates of the new ends.
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
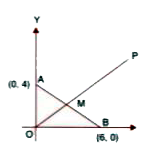
co-ordinates of M
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
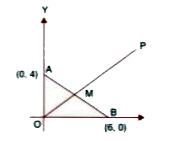
co-ordinates of P
View SolutionA line segment joining A(−1,53) and B(a, 5) is divided in the ratio 1: 3 at P, the point where the line segment AB intersects the y-axis.
Calculate the co-ordinates of 'P'.
View SolutionFind the ratio in which the line segment having the end points A(−1,−3,4) and B(4,2,−1) is divided by the xz−plane. Also, find the coordinates of the point of division.
View SolutionIf a point P lies on the line segment joining points A(−3,4)andB(−2,−6) such that 2AP=3BP
then, find the co-ordinates of point P.
View SolutionGiven a line segment AB joining the points A (-4, 6) and B (8, -3). Find :
(iii) the length of AB.
View SolutionDraw a line segment of length √3 cm.
View SolutionThe length of a line segment joining A(2, −3) and B is 10 units. If the abscissa of B is 10 units, then its ordinates can be (a) 3 or −9 (b) −3 or 9 (c) 6 or 27 (d) −6 or −27
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
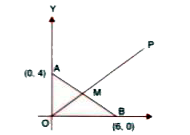
length of BP
View Solution
