A line segment joining A(−1,53) and B(a, 5) is divided in the ratio 1: 3 at P, the point where the line segment AB intersects the y-axis.
Calculate the co-ordinates of 'P'.
To find the coordinates of point P, where the line segment AB intersects the y-axis and divides the segment in the ratio 1:3, we can use the section formula. The coordinates of points A and B are given as A(-1, 5/3) and B(a, 5).
1. Identify the Coordinates:
- Point A has coordinates (-1, 5/3).
- Point B has coordinates (a, 5).
- Point P is the point where the line segment AB intersects the y-axis, so its x-coordinate is 0. We need to find its y-coordinate, which we will denote as y.
2. Use the Section Formula:
The section formula states that if a point P divides the line segment joining points A(x1, y1) and B(x2, y2) in the ratio m:n, then the coordinates of point P are given by:
P(mx2+nx1m+n,my2+ny1m+n)
In our case, m = 1, n = 3, and we have:
- x1=−1, y1=53
- x2=a, y2=5
3. Calculate the x-coordinate of P:
Since P lies on the y-axis, its x-coordinate is 0. Therefore, we set up the equation:
0=1⋅a+3⋅(−1)1+3
Simplifying this gives:
0=a−34
From this, we find:
a−3=0⟹a=3
4. Calculate the y-coordinate of P:
Now we can find the y-coordinate using the section formula:
y=1⋅5+3⋅531+3
Simplifying this:
y=5+54=104=52
5. Final Coordinates of P:
Therefore, the coordinates of point P are:
P(0,52)
Conclusion:
The coordinates of point P, where the line segment AB intersects the y-axis, are P(0,52).
- Point A has coordinates (-1, 5/3).
- Point B has coordinates (a, 5).
- Point P is the point where the line segment AB intersects the y-axis, so its x-coordinate is 0. We need to find its y-coordinate, which we will denote as y.
The section formula states that if a point P divides the line segment joining points A(x1, y1) and B(x2, y2) in the ratio m:n, then the coordinates of point P are given by:
P(mx2+nx1m+n,my2+ny1m+n)
In our case, m = 1, n = 3, and we have:
- x1=−1, y1=53
- x2=a, y2=5
Since P lies on the y-axis, its x-coordinate is 0. Therefore, we set up the equation:
0=1⋅a+3⋅(−1)1+3
Simplifying this gives:
0=a−34
From this, we find:
a−3=0⟹a=3
Now we can find the y-coordinate using the section formula:
y=1⋅5+3⋅531+3
Simplifying this:
y=5+54=104=52
Therefore, the coordinates of point P are:
P(0,52)
The coordinates of point P, where the line segment AB intersects the y-axis, are P(0,52).
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS17videos
SECTION AND MID-POINT FORMULA
- BOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (B)20videos
SECTION AND MID-POINT FORMULA
- BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C8videos
SAMPLE PAPER 5 (MATHEMATICS)
- BOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )20videos
SHARES AND DIVIDENDS
Similar Questions
A line segment joining A(−1,53) and B(a, 5) is divided in the ratio 1: 3 at P, the point where the line segment AB intersects the y-axis.
Calculate the value of a'.View SolutionIn what ratio is the line joining A(0, 3) and B(4, -1) divided by the x-axis ?
Write the co-ordinates of the point where AB intersects the x-axis.View SolutionThe co-ordinates of two points A and B are (-3, 4) and (2, -1). Find :
the co-ordinates of the point where the line AB intersects the y-axis.View SolutionIf P (9a-2,-b) divides line segment joining A (3a+1,-3) and B(8a,5) in the ratio 3:1, then find the values of a and b.
View SolutionThe line segment joining the points A(3,2) and B (5,1) is divided at the point P in the ratio 1:2 and it lies on the line 3x−18y+k=0. Find the value of k.
View SolutionThe line segment joining the points A (3,-4) and B (-2, 1) is divided in the ratio 1:3 at point P in it. Find the co-ordinates of P.
Also, find the equation of the line through P and perpendicular to the line 5x–3y=4.View SolutionThe mid - point of line segment AB (shown in the diagram) is (-3, 5), Find the co-ordinates of A and B.
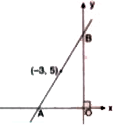 . View Solution
. View SolutionIn ΔABC, a point P on BC divided BC in the ratio 1:1. what is the line segment joining vertex A and P called ?
View SolutionA line perpendicular to the in segment joining the points (1,0) and (2,3) divides it in the ratio 1:n . Find the equation of the line.
View SolutionGiven a line segment AB joining the points A (-4, 6) and B (8, -3). Find :
(ii) find the coordinates of the point of intersection. Divided by y-axis.View Solution

