If R be circum-radius of aΔ, then circum-radius of a pedal Δ is
R
2R3
R3
R2
The correct Answer is:D
To find the circum-radius of the pedal triangle DEF in relation to the circum-radius R of triangle ABC, we can follow these steps:
Step 1: Understand the Geometry
We have a triangle ABC with circum-radius R. The pedal triangle DEF is formed by dropping perpendiculars from the vertices A,B,C to the opposite sides BC,CA,AB respectively.
Hint: Visualize the triangle and the pedal triangle by sketching it out. Label the points clearly.
Step 2: Identify the Orthocenter
The orthocenter H of triangle ABC is the point where the altitudes intersect. The pedal triangle DEF has its vertices at the feet of the altitudes from A,B,C.
Hint: Remember that the orthocenter is an important point in triangle geometry and affects the relationships between the triangles.
Step 3: Use the Cosine Rule
In triangle AFE (where F is the foot of the altitude from A), we can apply the cosine rule. Let a,b,c be the lengths of sides BC,CA,AB respectively.
Using the cosine rule in triangle AFE:
AF2=AB2+AE2−2⋅AB⋅AE⋅cos(A)
where AF=ha (the altitude from A).
Hint: Recall the cosine rule: c2=a2+b2−2abcos(C).
Step 4: Relate the Sides to the Circumradius
The circum-radius R of triangle ABC is given by:
R=abc4K
where K is the area of triangle ABC.
Hint: The circumradius is a function of the sides and area of the triangle.
Step 5: Find the Circumradius of the Pedal Triangle
The circumradius R′ of the pedal triangle DEF can be shown to be:
R′=R2
This is derived from the relationships established in the previous steps and the properties of the angles in the pedal triangle.
Hint: Look for relationships between the angles in triangle ABC and triangle DEF.
Conclusion
Thus, the circum-radius of the pedal triangle DEF is:
R′=R2
We have a triangle ABC with circum-radius R. The pedal triangle DEF is formed by dropping perpendiculars from the vertices A,B,C to the opposite sides BC,CA,AB respectively.
The orthocenter H of triangle ABC is the point where the altitudes intersect. The pedal triangle DEF has its vertices at the feet of the altitudes from A,B,C.
In triangle AFE (where F is the foot of the altitude from A), we can apply the cosine rule. Let a,b,c be the lengths of sides BC,CA,AB respectively.
AF2=AB2+AE2−2⋅AB⋅AE⋅cos(A)
where AF=ha (the altitude from A).
The circum-radius R of triangle ABC is given by:
R=abc4K
where K is the area of triangle ABC.
The circumradius R′ of the pedal triangle DEF can be shown to be:
R′=R2
This is derived from the relationships established in the previous steps and the properties of the angles in the pedal triangle.
Thus, the circum-radius of the pedal triangle DEF is:
R′=R2
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Video
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
The in-radius of pedal Δ of a ΔABC is
View SolutionIf R be the circum radius and r the in radius of a triangle ABC, show that R≥2r
View SolutionIn an acute angle ΔABC, let AD, BE and CF be the perpendicular from A, B and C upon the opposite sides of the triangle. (All symbols used have usual meaning in a tiangle.)
The circum-radius of the ΔDEF can be equal to
View SolutionFind the ratio of the circum-radius and the inradius of ΔABC, whose sides are in the ratio 4:5:6.
View SolutionConsider a triangle ABC, and that AA', BB', CC' be the perpendicular form A, B and C upon the sides opposite to them. These three perpendicualrs meets in H, called the orthocenter of the triangle.The triangle A'B'C' formed by the feet of the perpendicular is called the pedal triangle of ABC. (Assume ∠A,B,C≠90∘)
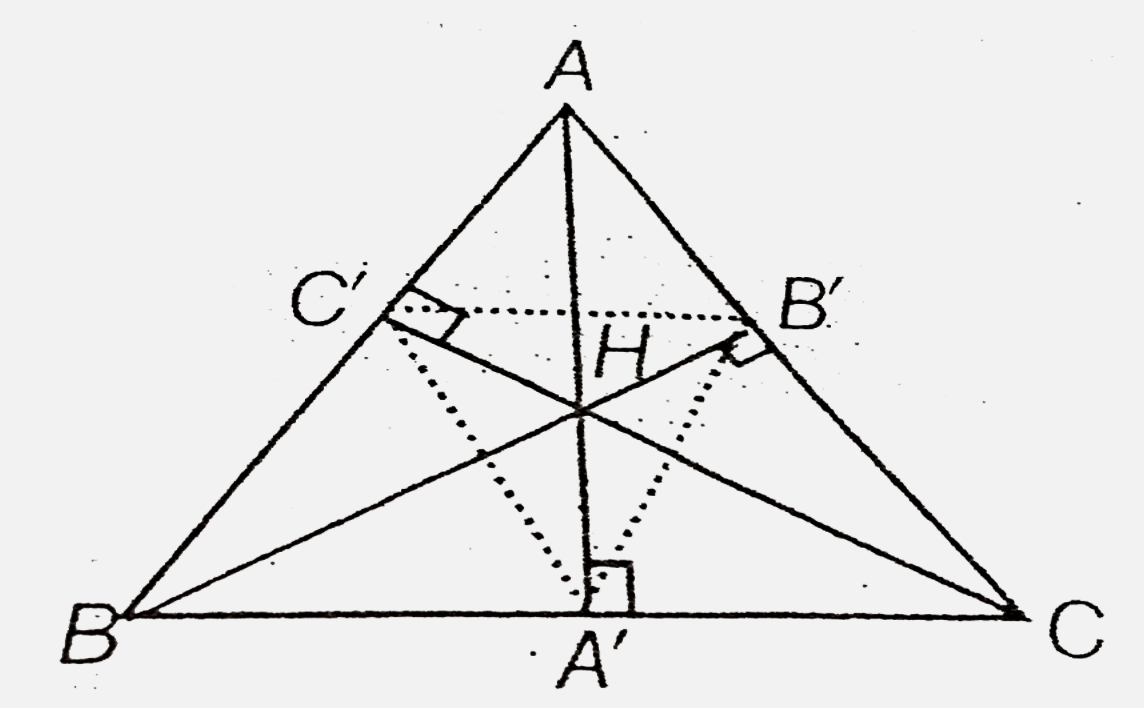
Suppose a triangle ABC has its sides 13, 14 and 15 cm. Then the circumradius of the pedal triangles is (in cm)
View SolutionIf circum-radius and in-radius of a triangle ABC be 10 and 3 units respectively , then a cot A +b cot B +c cot C is equal to
View Solutionif sum of two sides of a triangle is x and the product of those sides is y and third side is c such that x2−c2=y then circum radius of Δ is (A) y√3 (B) c√3 (C) 3y4 (D)3c4
View SolutionFind the Side of pedal triangle and Circum-Radius of pedal Triangle ?
View SolutionThe angle of elevation of the top of the tower observed from each of three points A,B , C on the ground, forming a triangle is the same angle α. If R is the circum-radius of the triangle ABC, then find the height of the tower
View SolutionIf R1 is the circumradius of the pedal triangle of a given triangle ABC, and R2 is the circumradius of the pedal triangle of the pedal triangle formed, and so on R3,R4..., then the value of ∞∑i=1Ri, where R (circumradius) of ΔABC is 5 is
View Solution