If the lengths of the side of a triangle are 3,4 and 5 units, then find the circum radius R.
To find the circumradius R of a triangle with sides a=3, b=4, and c=5, we can use two approaches. Let's go through the steps for both methods.
Method 1: Using the property of right triangles
1. Identify the triangle type:
We check if the triangle is a right triangle using the Pythagorean theorem:
a2+b2=c2
Substituting the values:
32+42=52⟹9+16=25⟹25=25
Since this holds true, the triangle is a right triangle.
2. Use the circumradius formula for right triangles:
For a right triangle, the circumradius R is given by:
R=c2
where c is the hypotenuse. Here, c=5:
R=52=2.5
Method 2: Using the general formula for circumradius
1. Calculate the area of the triangle:
The area A of a right triangle can be calculated using:
A=12×base×height
Here, we can take a=3 as the base and b=4 as the height:
A=12×3×4=6
2. Use the general formula for circumradius:
The circumradius R can also be calculated using the formula:
R=abc4A
Substituting the values a=3, b=4, c=5, and A=6:
R=3×4×54×6
Simplifying this:
R=6024=52=2.5
Final Answer:
Thus, the circumradius R of the triangle is 2.5 units.
---
We check if the triangle is a right triangle using the Pythagorean theorem:
a2+b2=c2
Substituting the values:
32+42=52⟹9+16=25⟹25=25
Since this holds true, the triangle is a right triangle.
For a right triangle, the circumradius R is given by:
R=c2
where c is the hypotenuse. Here, c=5:
R=52=2.5
The area A of a right triangle can be calculated using:
A=12×base×height
Here, we can take a=3 as the base and b=4 as the height:
A=12×3×4=6
The circumradius R can also be calculated using the formula:
R=abc4A
Substituting the values a=3, b=4, c=5, and A=6:
R=3×4×54×6
Simplifying this:
R=6024=52=2.5
Thus, the circumradius R of the triangle is 2.5 units.
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 4
10 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 5
7 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 2
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
If the lengths of the sides of a triangle are 8, 15 and 17 units, the R the circum-radius is :
View SolutionIf the sides of a triangle are 3,5 and 7, then find cos A
View SolutionIf the middle points of the sides of a triangle are (−2,3),(4,−3),and(4,5) , then find the centroid of the triangle.
View SolutionFind the length of the third side of the triangle.
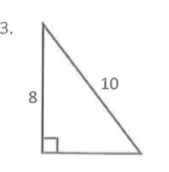
View SolutionFind the length of the third side of the triangle.
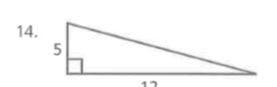
View SolutionIf the lengths of the sides of a triangle are 3,5,7, then its largest angle of the triangle is
View SolutionIf area of a triangle is 2 sq. units, then find the value of the product of the arithmetic mean of the lengths of the sides of a triangle and harmonic mean of the lengths of the altitudes of the triangle.
View SolutionIf area of a triangle is 2 sq. units, then find the value of the product of the arithmetic mean of the lengths of the sides of a triangle and harmonic mean of the lengths of the altitudes of the triangle.
View SolutionIf the sides of a triangle are in the ratio 3:7:8, then find R:r
View SolutionThe lengths of the sides of a triangle are in the ration 3:4:5 and its perimeter is 144cm. Find the area of the triangle and the height corresponding to the longest side.
View Solution
