If area of a triangle is 2 sq. units, then find the value of the product of the arithmetic mean of the lengths of the sides of a triangle and harmonic mean of the lengths of the altitudes of the triangle.
To solve the problem, we need to find the product of the arithmetic mean of the lengths of the sides of a triangle and the harmonic mean of the lengths of the altitudes of the triangle, given that the area of the triangle is 2 square units.
1. Define the sides of the triangle:
Let the lengths of the sides of the triangle be a, b, and c.
2. Calculate the Arithmetic Mean (AM):
The arithmetic mean of the lengths of the sides is given by:
AM=a+b+c3
3. Define the altitudes of the triangle:
Let the altitudes corresponding to sides a, b, and c be h1, h2, and h3 respectively.
4. Relate the area to the sides and altitudes:
The area A of the triangle can be expressed using the formula:
A=12×base×height
Thus, we have:
A=12×a×h1=12×b×h2=12×c×h3
Since the area A is given as 2 square units, we can write:
2=12×a×h1⟹a×h1=4
2=12×b×h2⟹b×h2=4
2=12×c×h3⟹c×h3=4
5. Find the sum of the reciprocals of the altitudes:
From the equations above, we can express the altitudes in terms of the sides:
h1=4a,h2=4b,h3=4c
Therefore, the sum of the reciprocals of the altitudes is:
1h1+1h2+1h3=a4+b4+c4=a+b+c4
6. Calculate the Harmonic Mean (HM):
The harmonic mean of the lengths of the altitudes is given by:
HM=31h1+1h2+1h3=3×4a+b+c=12a+b+c
7. Calculate the product of AM and HM:
Now we need to find the product of the arithmetic mean and harmonic mean:
Product=AM×HM=(a+b+c3)×(12a+b+c)
Simplifying this gives:
Product=123=4
Final Answer:
Thus, the value of the product of the arithmetic mean of the lengths of the sides of the triangle and the harmonic mean of the lengths of the altitudes of the triangle is 4.
Let the lengths of the sides of the triangle be a, b, and c.
The arithmetic mean of the lengths of the sides is given by:
AM=a+b+c3
Let the altitudes corresponding to sides a, b, and c be h1, h2, and h3 respectively.
The area A of the triangle can be expressed using the formula:
A=12×base×height
Thus, we have:
A=12×a×h1=12×b×h2=12×c×h3
Since the area A is given as 2 square units, we can write:
2=12×a×h1⟹a×h1=4
2=12×b×h2⟹b×h2=4
2=12×c×h3⟹c×h3=4
From the equations above, we can express the altitudes in terms of the sides:
h1=4a,h2=4b,h3=4c
Therefore, the sum of the reciprocals of the altitudes is:
1h1+1h2+1h3=a4+b4+c4=a+b+c4
The harmonic mean of the lengths of the altitudes is given by:
HM=31h1+1h2+1h3=3×4a+b+c=12a+b+c
Now we need to find the product of the arithmetic mean and harmonic mean:
Product=AM×HM=(a+b+c3)×(12a+b+c)
Simplifying this gives:
Product=123=4
Thus, the value of the product of the arithmetic mean of the lengths of the sides of the triangle and the harmonic mean of the lengths of the altitudes of the triangle is 4.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.112videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.28videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
The product of the arithmetic mean of the lengths of the sides of a triangle and harmonic mean of the lengths of the altitudes of the triangle is equal to: a. 1 b. 2 c. 3 d. 4
View SolutionFind the length of the third side of the triangle.
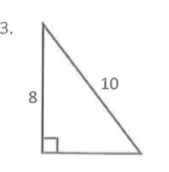 View Solution
View SolutionFind the length of the third side of the triangle.
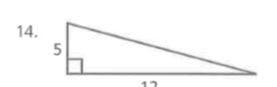 View Solution
View SolutionIf the lengths of the sides of a triangle are 8, 15 and 17 units, the R the circum-radius is :
View SolutionIf the sides of a triangle are 17,25and28, then find the greatest length of the altitude.
View SolutionIf the sides of a triangle are 17,25and28, then find the greatest length of the altitude.
View SolutionFind the length of side BC in the given triangle.
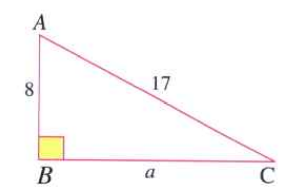 View Solution
View SolutionIf the lengths of the side of a triangle are 3,4 and 5 units, then find the circum radius R.
View SolutionThe lengths of the sides of a triangle are in the ratio 2:3:4. If the perimeter of the triangle is 63 cm, find the lengths of the sides of the triangle.
View SolutionIf the altitudes of a triangle are in A.P,then the sides of the triangle are in
View Solution

