Statement I :Among all the rectangles of the given perimeter, the square has the largest area. Also among all the rectangles of given area, the square has the least perimeter.
Statement II :For x>0,y>0,ifx+y= constant, then xy will be maximum for y=x and if xy=constant, then x+y will be minimum for y=x.
Statement I is true, Statement II is also true, Statement II is the correct explanation of statement I.
Statemetn I is true, Statement II is also true, Statement II is not correct explanation of Statement I
Statement I is true, Statement II is false
Statement I is false, Statement II is true
To solve the problem, we need to analyze the two statements provided and verify their correctness step-by-step.
Step 1: Analyze Statement I
Statement I: Among all the rectangles of a given perimeter, the square has the largest area. Also, among all the rectangles of a given area, the square has the least perimeter.
1. Given: Let the perimeter P of a rectangle be constant. The perimeter of a rectangle is given by:
P=2(x+y)
where x and y are the lengths of the sides of the rectangle.
2. Express y in terms of x:
y=P2−x
3. Area A of the rectangle:
A=x⋅y=x(P2−x)=P2x−x2
4. To find the maximum area, differentiate A with respect to x:
dAdx=P2−2x
5. Set the derivative to zero to find critical points:
P2−2x=0⟹x=P4
6. Substituting x back to find y:
y=P2−P4=P4
7. Thus, the rectangle with maximum area is a square with sides P4.
8. Now, consider the second part of Statement I: Among all rectangles of a given area A, the square has the least perimeter.
9. Let the area A be constant. The perimeter P of a rectangle is given by:
P=2(x+y)
10. Express y in terms of x:
y=Ax
11. Substituting y into the perimeter equation:
P=2(x+Ax)
12. To minimize P, differentiate with respect to x:
dPdx=2(1−Ax2)
13. Set the derivative to zero:
1−Ax2=0⟹x2=A⟹x=√A
14. Thus, y=A√A=√A. The rectangle with minimum perimeter is also a square.
Conclusion for Statement I:
Both parts of Statement I are correct.
---
Step 2: Analyze Statement II
Statement II: For x>0,y>0, if x+y=c (constant), then xy will be maximum for y=x and if xy=k (constant), then x+y will be minimum for y=x.
1. First part of Statement II: Given x+y=c, we want to maximize xy.
2. Express y in terms of x:
y=c−x
3. Area function:
A=x(c−x)=cx−x2
4. Differentiate A:
dAdx=c−2x
5. Set the derivative to zero:
c−2x=0⟹x=c2
6. Then y=c−x=c2. Thus, x=y maximizes xy.
7. Second part of Statement II: Given xy=k (constant), we want to minimize x+y.
8. Express y in terms of x:
y=kx
9. Minimize x+y:
P=x+kx
10. Differentiate P:
dPdx=1−kx2
11. Set the derivative to zero:
1−kx2=0⟹x2=k⟹x=√k
12. Then y=k√k=√k. Thus, x=y minimizes x+y.
Conclusion for Statement II:
Both parts of Statement II are correct.
---
Final Conclusion:
Both Statement I and Statement II are correct. Therefore, the answer is that both statements are true.
---
Statement I: Among all the rectangles of a given perimeter, the square has the largest area. Also, among all the rectangles of a given area, the square has the least perimeter.
P=2(x+y)
where x and y are the lengths of the sides of the rectangle.
y=P2−x
A=x⋅y=x(P2−x)=P2x−x2
dAdx=P2−2x
P2−2x=0⟹x=P4
y=P2−P4=P4
P=2(x+y)
y=Ax
P=2(x+Ax)
dPdx=2(1−Ax2)
1−Ax2=0⟹x2=A⟹x=√A
Both parts of Statement I are correct.
Statement II: For x>0,y>0, if x+y=c (constant), then xy will be maximum for y=x and if xy=k (constant), then x+y will be minimum for y=x.
y=c−x
A=x(c−x)=cx−x2
dAdx=c−2x
c−2x=0⟹x=c2
y=kx
P=x+kx
dPdx=1−kx2
1−kx2=0⟹x2=k⟹x=√k
Both parts of Statement II are correct.
Both Statement I and Statement II are correct. Therefore, the answer is that both statements are true.
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - EXAMPLE23videos
MONOTONICITY MAXIMA AND MINIMA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise For Session 17videos
MONOTONICITY MAXIMA AND MINIMA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)49videos
MATRICES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)2videos
PAIR OF STRAIGHT LINES
Similar Questions
Show that all the rectangles with a given perimeter, the square has the largest area.
View SolutionShow that all the rectangles with a given perimeter, the square has the largest area.
View SolutionShow that of all the rectangles of given area, the square has the smallest perimeter.
View SolutionShow that of all the rectangles inscribed in a given circle, the square has the maximum area.
View SolutionShow that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
View SolutionShow that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
View SolutionThe largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
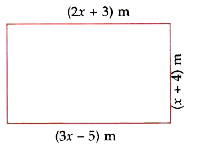
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
 View Solution
View SolutionFind the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12−x2.
View SolutionFind the area of the largest rectangle in the first quadrant with two sides on x-axis and y-axis and one vertex on the curve y=12−x2
View Solution

