In $△ A B C$ , D is the mid point of the side AB and E is centroid of $△ C D A$ . If $O E \cdot C D = 0$ , where O is the circumcentre of $△ A B C$ , using vectors prove that AB=AC.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem step by step using vectors, we will follow the instructions given in the video transcript.
1. Define the Points and Vectors:
Let $O$ be the circumcenter of triangle $A B C$ , and we can set $O$ as the origin. Thus, we have:
- $\to A = \to a$
- $\to B = \to b$
- $\to C = \to c$
2. Identify the Midpoint D:
Since $D$ is the midpoint of $A B$ , we can express $\to D$ as:
$\to D = \frac{\to A + \to B}{2} = \frac{\to a + \to b}{2}$
3. Find the Centroid E of Triangle CDA:
The centroid $E$ of triangle $C D A$ can be calculated using the formula for the centroid, which is the average of the position vectors of the vertices:
$\to E = \frac{\to C + \to D + \to A}{3}$
Substituting $\to D$ :
$\to E = \frac{\to C + \frac{\to A + \to B}{2} + \to A}{3} = \frac{\to C + \frac{2 \to A + \to B}{2}}{3} = \frac{\to C + \to A + \frac{\to B}{2}}{3}$
4. Use the Condition OE · CD = 0:
The condition given is $\to O E \cdot \to C D = 0$ . We can express $\to O E$ as:
$\to O E = \to E - \to O = \to E$
Since $O$ is the origin, we have:
$\to O E = \to E$
Now, $\to C D = \to D - \to C$ :
$\to C D = \frac{\to A + \to B}{2} - \to C$
5. Calculate the Dot Product:
The dot product $\to O E \cdot \to C D = 0$ implies:
$\to E \cdot (\frac{\to A + \to B}{2} - \to C) = 0$
Expanding this gives:
$⎛ ⎜ ⎝ \frac{\to C + \to A + \frac{\to B}{2}}{3} ⎞ ⎟ ⎠ \cdot (\frac{\to A + \to B}{2} - \to C) = 0$
6. Simplify and Rearrange:
After simplification, we will find that:
$4 \to A \cdot \to B = 4 \to C \cdot \to A$
Dividing by 4 gives:
$\to A \cdot \to B = \to C \cdot \to A$
7. Conclude that AB = AC:
The equality $\to A \cdot \to B = \to C \cdot \to A$ indicates that the lengths of the sides opposite to angles $B$ and $C$ are equal, which implies:
$A B = A C$

Updated on:7/8/2024

|

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

Knowledge Check

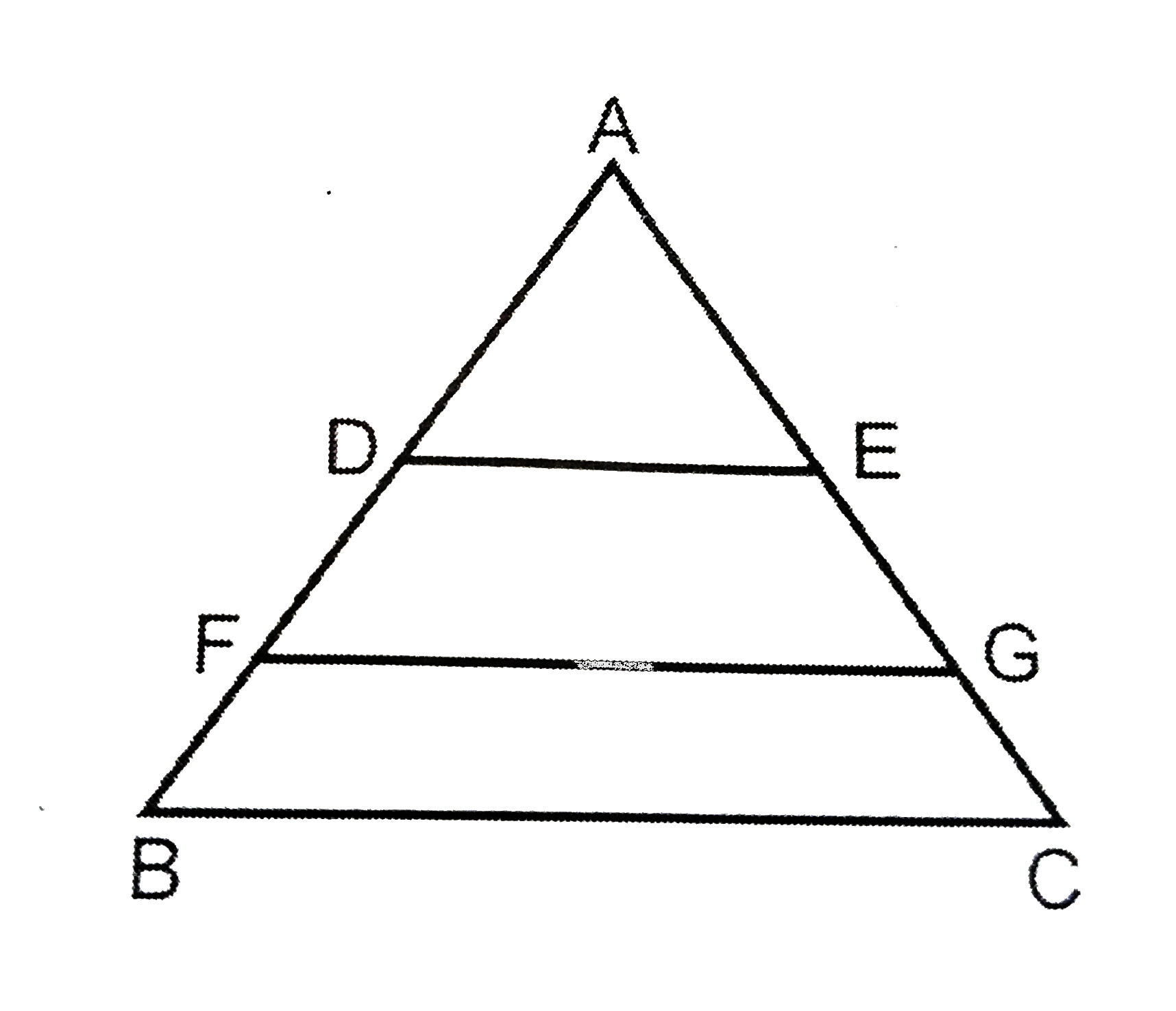
In $Δ A B C$ ,D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC, If BC=12,what is the length of FG?
A4
B6
C8
D9

ARIHANT MATHS ENGLISH-PRODUCT OF VECTORS-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile