a×(b×c) is coplanar with
b and c
a and c
a and b are unlike vectors
a, b and c
The correct Answer is:A
To determine which vectors are coplanar with the vector D=A×(B×C), we can use the properties of the scalar triple product. The scalar triple product of three vectors X,Y,Z is given by X⋅(Y×Z), and it is equal to zero if the vectors are coplanar.
1. Define the Vector D:
D=A×(B×C)
Using the vector triple product identity, we can express D as:
D=(A⋅C)B−(A⋅B)C
2. Check Option A: Vectors B and C:
To check if D is coplanar with B and C, we calculate the scalar triple product D⋅(B×C):
D⋅(B×C)=((A⋅C)B−(A⋅B)C)⋅(B×C)
Expanding this gives:
=(A⋅C)(B⋅(B×C))−(A⋅B)(C⋅(B×C))
Both terms are zero because B⋅(B×C)=0 and C⋅(B×C)=0. Thus:
D⋅(B×C)=0
Therefore, D is coplanar with B and C.
3. Check Option B: Vectors A and C:
We check if D is coplanar with A and C by calculating D⋅(A×C):
D⋅(A×C)=((A⋅C)B−(A⋅B)C)⋅(A×C)
This expands to:
=(A⋅C)(B⋅(A×C))−(A⋅B)(C⋅(A×C))
The first term is zero since B⋅(A×C) is not guaranteed to be zero, and the second term is zero because C⋅(A×C)=0. Thus, D is not coplanar with A and C.
4. Check Option C: Vectors A and B:
We check if D is coplanar with A and B:
D⋅(A×B)=((A⋅C)B−(A⋅B)C)⋅(A×B)
This expands to:
=(A⋅C)(B⋅(A×B))−(A⋅B)(C⋅(A×B))
The first term is zero, and the second term is not guaranteed to be zero. Thus, D is not coplanar with A and B.
5. Check Option D: Vectors A, B, and C:
Since we have already established that D is coplanar with B and C but not with A, it follows that D is not coplanar with all three vectors A,B,C.
Conclusion:
The only option that is correct is Option A: Vectors B and C.
D=A×(B×C)
Using the vector triple product identity, we can express D as:
D=(A⋅C)B−(A⋅B)C
To check if D is coplanar with B and C, we calculate the scalar triple product D⋅(B×C):
D⋅(B×C)=((A⋅C)B−(A⋅B)C)⋅(B×C)
Expanding this gives:
=(A⋅C)(B⋅(B×C))−(A⋅B)(C⋅(B×C))
Both terms are zero because B⋅(B×C)=0 and C⋅(B×C)=0. Thus:
D⋅(B×C)=0
Therefore, D is coplanar with B and C.
We check if D is coplanar with A and C by calculating D⋅(A×C):
D⋅(A×C)=((A⋅C)B−(A⋅B)C)⋅(A×C)
This expands to:
=(A⋅C)(B⋅(A×C))−(A⋅B)(C⋅(A×C))
The first term is zero since B⋅(A×C) is not guaranteed to be zero, and the second term is zero because C⋅(A×C)=0. Thus, D is not coplanar with A and C.
We check if D is coplanar with A and B:
D⋅(A×B)=((A⋅C)B−(A⋅B)C)⋅(A×B)
This expands to:
=(A⋅C)(B⋅(A×B))−(A⋅B)(C⋅(A×B))
The first term is zero, and the second term is not guaranteed to be zero. Thus, D is not coplanar with A and B.
Since we have already established that D is coplanar with B and C but not with A, it follows that D is not coplanar with all three vectors A,B,C.
The only option that is correct is Option A: Vectors B and C.
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (More Than One Correct Option Type Questions)
35 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Statement I And Ii Type Questions)
12 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 4
10 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
If a, b and c are any three non-zero vectors, then the component of a×(b×c) perpendicular to b is
View SolutionLet a, b and c are non-zero vectors such that they are not orthogonal pairwise and such that V1=a×(b×c)andV2=(a×b)×c,are collinear then which of the following holds goods?
Option1. a and b are orthogonal
Option 2. a and c are collinear
Option 3. b and c are orthogonal
Option 4. b=λ(a×c) when λ is a scalar
View Solution
Knowledge Check
In which of the following molecules −NO2 group is not coplanar with phenyl ring?
A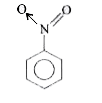 B
B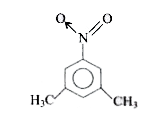 C
C D
D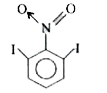
If a×(b×c)=0, then
View SolutionIf a=ˆi+2ˆj−2ˆk,b=2ˆi−ˆj+ˆkandc=ˆi+3ˆj−ˆk, then a×(b×c) is equal to
View SolutionIf →aand→b are othogonal unit vectors, then for a vector →r non - coplanar with →aand→b vector →r×→a is equal to
View SolutionLet a=αˆi+2ˆj−3ˆk,b=ˆi+2αˆj−2ˆkandc=2ˆi−αˆj+ˆk. Then the value of 6α, such that {(a×b)×(b×c)}×(c×a)=a, is
View SolutionVolume of parallelopiped formed by vectors a×b,b×candc×a is 36 sq.units. then the volumn formed by the vector a b and c is
View SolutionGiven, two vectors are ˆi−ˆj and ˆi+2ˆj, the unit vector coplanar with the two vectors and perpendicular to first is:
View SolutionIf a, b and c are non-collinear unit vectors also b, c are non-collinear and 2a×(b×c)=b+c, then
View Solution
