[Find by vector method the horizontal force and the force inclined at an angle of 60∘ to the vertical whose resultant is a vertical force P.]
P,2P
P,P√3
2P,P√3
None of these
The correct Answer is:D
To solve the problem of finding the horizontal force (F1) and the force inclined at an angle of 60 degrees to the vertical (F2) such that their resultant is a vertical force P, we can follow these steps:
1. Draw the Diagram:
- Draw a vertical line representing the vertical force P.
- Draw a horizontal force F1 to the right.
- Draw the force F2 inclined at 60 degrees to the vertical. This means that F2 makes a 30-degree angle with the horizontal.
2. Resolve the Forces:
- The vertical component of F2 can be expressed as:
F2cos(60∘)
- Since the resultant is a vertical force P, we can set up the equation:
P=F2cos(60∘)
3. Substitute the Value of Cosine:
- We know that cos(60∘)=12. Thus, we can rewrite the equation:
P=F2⋅12
4. Solve for F2:
- Rearranging the equation gives:
F2=2P
5. Find the Horizontal Force F1:
- The horizontal component of the force F2 can be expressed as:
F2sin(60∘)
- Since F1 is the horizontal force, we can write:
F1=F2sin(60∘)
6. Substitute the Value of Sine:
- We know that sin(60∘)=√32. Thus, we can substitute:
F1=(2P)⋅√32
7. Simplify the Expression for F1:
- This simplifies to:
F1=P√3
Final Answers:
- The horizontal force F1 is:
F1=P√3
- The force inclined at 60 degrees to the vertical F2 is:
F2=2P
- Draw a vertical line representing the vertical force P.
- Draw a horizontal force F1 to the right.
- Draw the force F2 inclined at 60 degrees to the vertical. This means that F2 makes a 30-degree angle with the horizontal.
- The vertical component of F2 can be expressed as:
F2cos(60∘)
- Since the resultant is a vertical force P, we can set up the equation:
P=F2cos(60∘)
- We know that cos(60∘)=12. Thus, we can rewrite the equation:
P=F2⋅12
- Rearranging the equation gives:
F2=2P
- The horizontal component of the force F2 can be expressed as:
F2sin(60∘)
- Since F1 is the horizontal force, we can write:
F1=F2sin(60∘)
- We know that sin(60∘)=√32. Thus, we can substitute:
F1=(2P)⋅√32
- This simplifies to:
F1=P√3
- The horizontal force F1 is:
F1=P√3
- The force inclined at 60 degrees to the vertical F2 is:
F2=2P
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (More Than One Correct Option Type Questions)
35 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Statement I And Ii Type Questions)
12 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 4
10 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
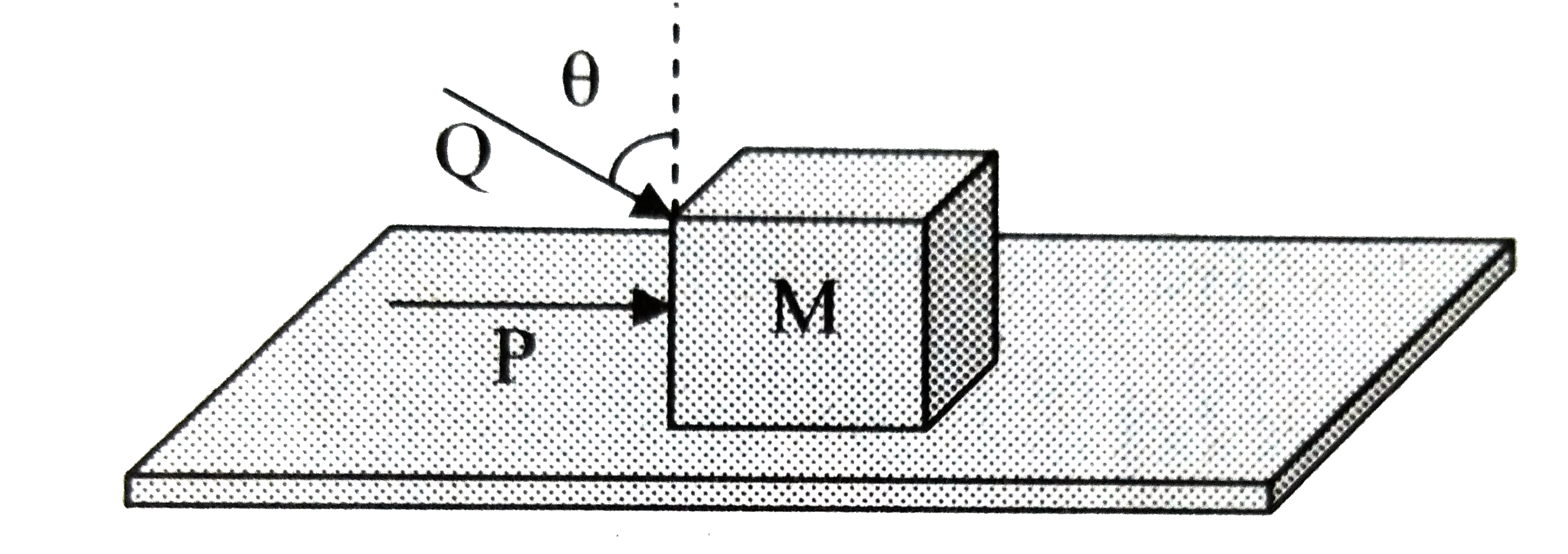
View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View Solution
A wedge of mass m, lying on a rough horizontal plane, is acted upon by a horizontal force F1 and another force F2, inclined at an angle θ to the vertical. The block is in equilibrium, then minimum coefficient of friction between it and te surface is
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionResolve horizontally and vertically a force f =8 N which makes an angle of 45∘ with the horizontal.
View Solution

