In the adjoining figure. AD and BE are two medians of ΔABC. IfDF||BE,then prove thatCF=14AC.
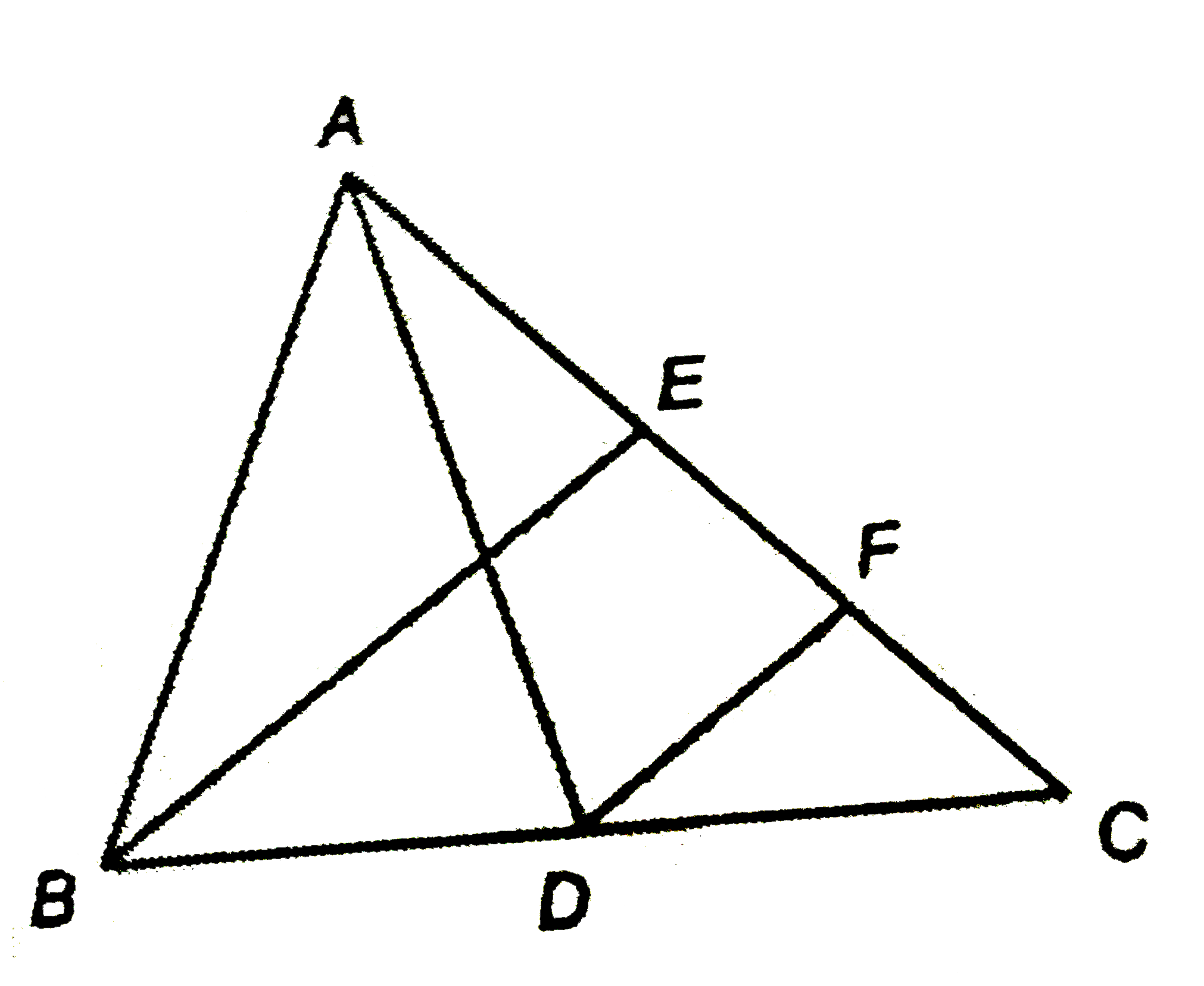
E is the mid-point of line AC.
∴CE=12AC ...(1)
In ΔABE,
Since, D is the mid-point of CB and DF||BE
∴F will be the mid-point of CE. (coverse of mid-point theorem)
⇒ CF=12CE
⇒ CF=12×12AC [from(1)]
⇒ CF=14AC
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise12videos
STATISTICS
Similar Questions
In the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
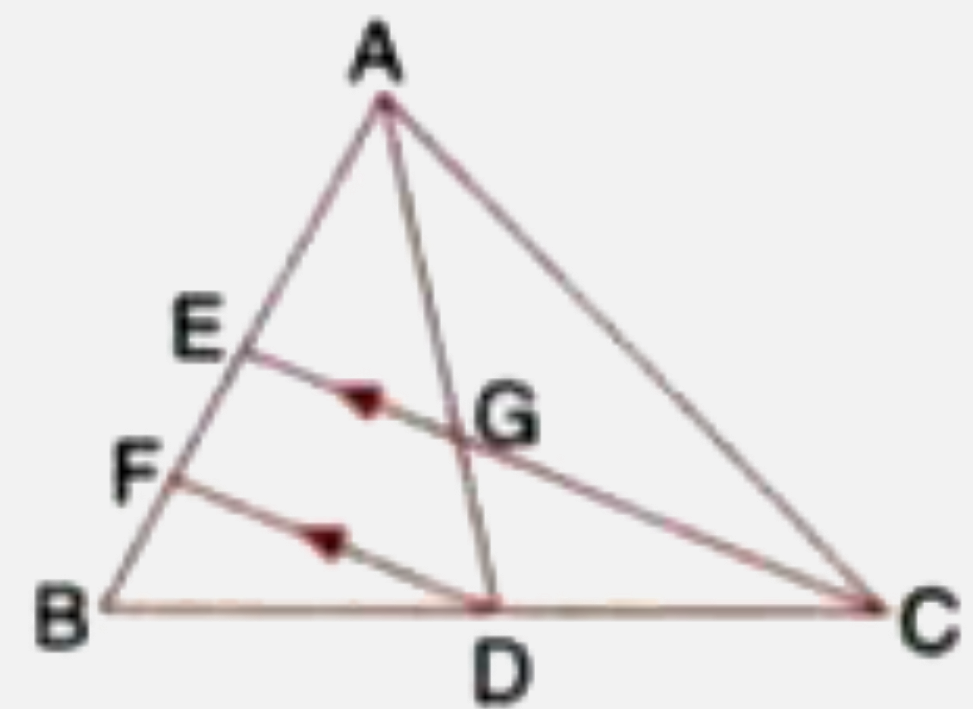
AG:GD=2:1.View SolutionIn the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :

EF=FBView SolutionFrom the adjoining figure, find the length of AC.
 View Solution
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)
 View Solution
View SolutionIn the adjoining figure, P is an interior point of ΔABC. Then prove that :
AB+BC+CA<2(PA+PB+PC)
 View Solution
View SolutionIn the given figure, AD and CE are medians and DF∣∣CE. Prove that : FB=14AB.
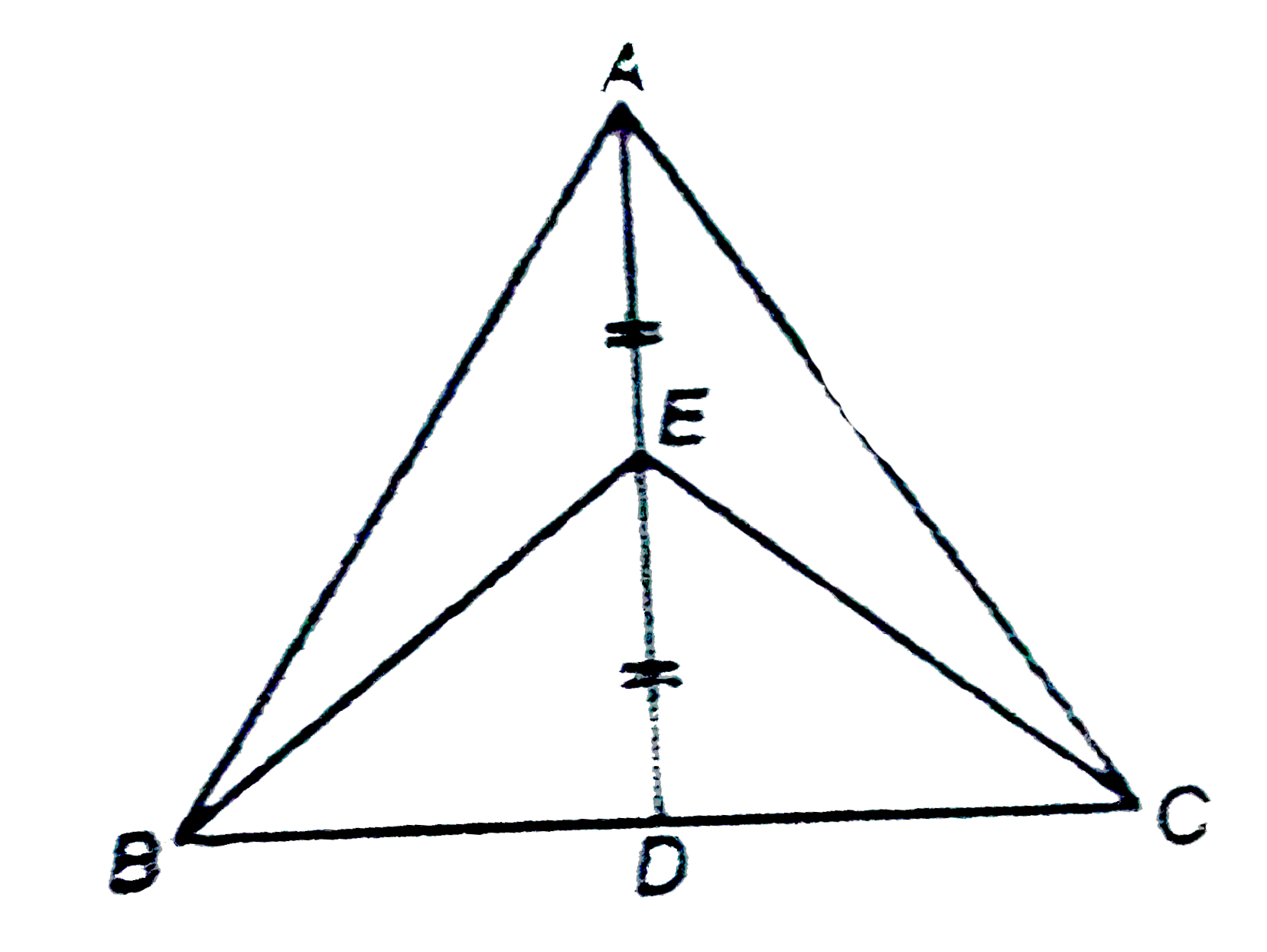
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
 View Solution
View SolutionIn the adjoining figure two medians AD and BE of a △ABC meet each other at O. prove that (i) △AOB~△DOE
View SolutionIn the following figure, BL = CM.

Prove that AD is a median of triangle ABC.View SolutionIn the adjoining figure, AD=DC and DB bisects ∠ADC. Prove that ΔADB≅ΔCDB.
 View Solution
View Solution

