The sun glasses have curved surfaces, but their power zero. Why?
To understand why sunglasses have curved surfaces but their power is zero, we can break down the explanation step by step.
Step 1: Understanding Lens Power
The power P of a lens is defined as the ability of the lens to converge or diverge light rays. It is given by the formula:
P=1F
where F is the focal length of the lens. A lens with zero power does not converge or diverge light rays.
Step 2: Lens Maker's Formula
The lens maker's formula relates the focal length of a lens to its radii of curvature and the refractive index. The formula is given by:
P=(n−1)(1R1−1R2)
where:
- n is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
Step 3: Equal Radii of Curvature
For sunglasses, the inner curvature (let's denote it as R1) is equal to the outer curvature (denote it as R2). Thus, we can write:
R1=R2
Step 4: Applying the Lens Maker's Formula
Substituting R1=R2 into the lens maker's formula, we get:
P=(n−1)(1R1−1R1)=(n−1)⋅0=0
Step 5: Conclusion
Since the power P is zero, this means that the sunglasses do not converge or diverge light rays. Therefore, even though they have curved surfaces, they are classified as zero power lenses.
Final Answer
Sunglasses have curved surfaces but their power is zero because the radii of curvature of both surfaces are equal, leading to a net power of zero according to the lens maker's formula.
---
The power P of a lens is defined as the ability of the lens to converge or diverge light rays. It is given by the formula:
P=1F
where F is the focal length of the lens. A lens with zero power does not converge or diverge light rays.
The lens maker's formula relates the focal length of a lens to its radii of curvature and the refractive index. The formula is given by:
P=(n−1)(1R1−1R2)
where:
- n is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
For sunglasses, the inner curvature (let's denote it as R1) is equal to the outer curvature (denote it as R2). Thus, we can write:
R1=R2
Substituting R1=R2 into the lens maker's formula, we get:
P=(n−1)(1R1−1R1)=(n−1)⋅0=0
Since the power P is zero, this means that the sunglasses do not converge or diverge light rays. Therefore, even though they have curved surfaces, they are classified as zero power lenses.
Sunglasses have curved surfaces but their power is zero because the radii of curvature of both surfaces are equal, leading to a net power of zero according to the lens maker's formula.
Similar Questions
Sun plants have
View SolutionStatement-I : Sun glasses have zero power even through their surfaces are curved.
and
Statement-II: Both surface of the sun glasses are curved in the same direction with same radii.
View SolutionWater on a clean glass surface, tends to spread out, while mercury on the same surface, tends to form drops. Why?
View SolutionThe edges of a surface are curves.
View SolutionA solid glass hemisphere of density d and radius R lies (with curved surface of hemisphere below the flat surface) at the bottom of a tank filled with water of density ρ such that the flat surface of hemisphere is H depth below the liquid surface. Weight of water + tank is W1 and that of hemisphere is'W2. W Then choose the incorrect options
View SolutionAssertion:Although the surfaces of goggle lens are curved, It does not have any power.
Reason: In case of goggles, both the curved surfaces have equal radii of curvature and have centre of curvature on the same side.
View SolutionAssertion:Although the surfaces of goggle lens are curved, It does not have any power.
Reason: In case of goggles, both the curved surfaces have equal radii of curvature and have centre of curvature on the same side.
View SolutionWhat should be the value of refractive index n of a glass rod placed in air, so that the light entering through the flat surface of the rod does not cross the curved surface of the rod?
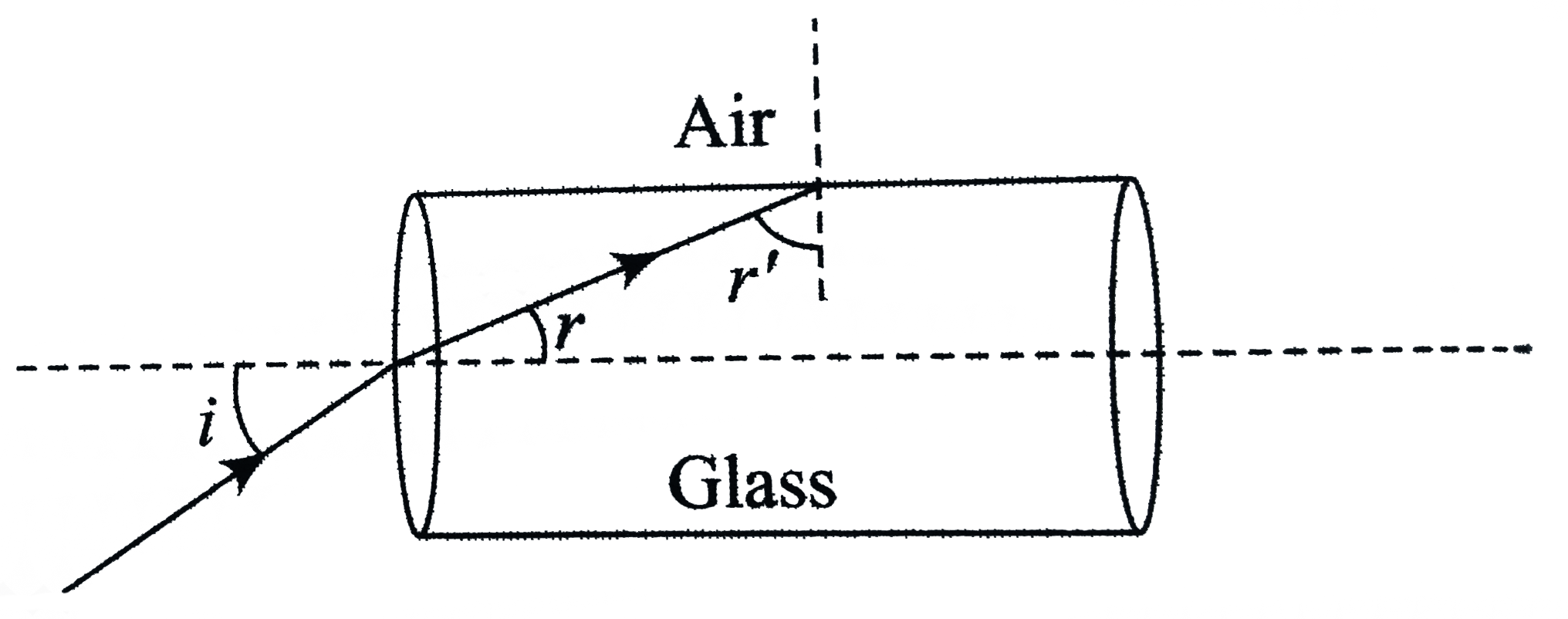
View SolutionProve that the surface area of a sphere is equal to the curved surface area of the circumscribed cylinder.
View SolutionA plano-concave lens is made of glass (R.l. = 1.5) and the radius of curvature of the curved face is 50 cm. The power of the lens is
View Solution