Statement-I : Sun glasses have zero power even through their surfaces are curved.
and
Statement-II: Both surface of the sun glasses are curved in the same direction with same radii.
Statement-I is true , Statement -II is true, Statement-II is correct explanation for Statement-I.
Statement - I is true, Statement -II is true: Statement -II is NOT a correct explanation for statement -I .
Statement-I is true, Statement-II is false.
statement-I is false, statement- II is true.
The correct Answer is:A
To solve the question, we need to analyze both statements regarding the sunglasses and their optical properties.
1. Understanding Statement I:
- Statement I claims that sunglasses have zero power despite their surfaces being curved.
- Power (P) of a lens is defined as the reciprocal of its focal length (F), given by the formula:
P=1F
- If the power is zero, it implies that the focal length is infinite (F = ∞).
2. Understanding Statement II:
- Statement II states that both surfaces of the sunglasses are curved in the same direction with the same radii.
- For a lens, the lens maker's formula is given by:
1F=(n−1)(1R1−1R2)
- Here, n is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the two surfaces.
3. Analyzing the Lens Maker's Formula:
- Since both surfaces are curved in the same direction and have the same radius of curvature, we can denote:
R1=RandR2=R
- Therefore, substituting into the lens maker's formula:
1F=(n−1)(1R−1R)=(n−1)⋅0=0
- This implies that 1F=0, hence F=∞.
4. Conclusion:
- Since the focal length is infinite, the power of the sunglasses is indeed zero.
- Therefore, both statements are true, and Statement II correctly explains Statement I.
Final Answer:
Both Statement I and Statement II are true, and Statement II provides the correct explanation for Statement I.
---
- Statement I claims that sunglasses have zero power despite their surfaces being curved.
- Power (P) of a lens is defined as the reciprocal of its focal length (F), given by the formula:
P=1F
- If the power is zero, it implies that the focal length is infinite (F = ∞).
- Statement II states that both surfaces of the sunglasses are curved in the same direction with the same radii.
- For a lens, the lens maker's formula is given by:
1F=(n−1)(1R1−1R2)
- Here, n is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the two surfaces.
- Since both surfaces are curved in the same direction and have the same radius of curvature, we can denote:
R1=RandR2=R
- Therefore, substituting into the lens maker's formula:
1F=(n−1)(1R−1R)=(n−1)⋅0=0
- This implies that 1F=0, hence F=∞.
- Since the focal length is infinite, the power of the sunglasses is indeed zero.
- Therefore, both statements are true, and Statement II correctly explains Statement I.
Both Statement I and Statement II are true, and Statement II provides the correct explanation for Statement I.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
47 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The sun glasses have curved surfaces, but their power zero. Why?
View SolutionStatement I: Surface tension has the same units as fore gradient.
Statement II: Surface tension is the force gradient along the surface of liquid.
View SolutionFind (i) the curved surface area and (ii) the total surface area of a hemisphere of radius 21 cm.
View SolutionStatement I: A body can have acceleration even if its velcity is zero at a given instant .
Statement II: A body is momentarily at rest when it reverses its direction of velocity.
View SolutionStatement I: Pulling is easier than pushing on a rough surface.
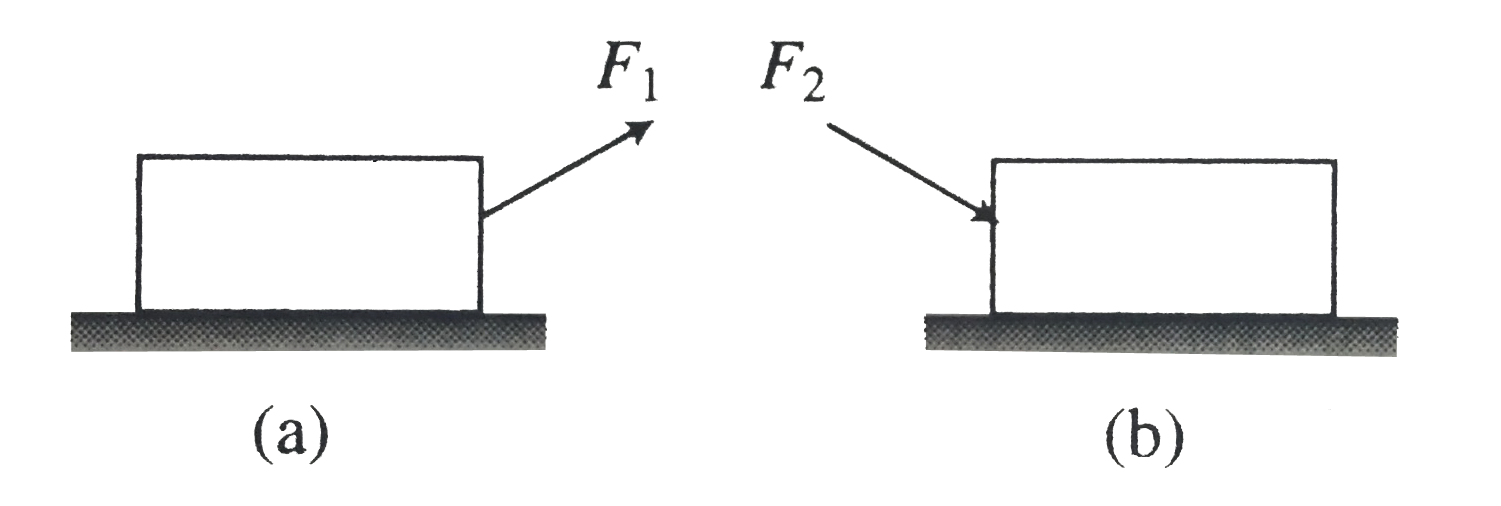
Statement II: Normal reaction is less in pulling than in pushing.
View SolutionWrite the negation of the following statements :
Both diagonals of a rectangle have the same length
View SolutionStatement-I A hyperbola and its conjugate hyperbola have the same asymptotes.
Statement-II The difference between the second degree curve and pair of asymptotes is constant.
View SolutionStatement-I: In practical application, power rating of resistance is not important.
Statement-II: Property of resistance remain same even at high temperature.
View SolutionWrite the negation of the following statement: Both the diagonals of a rectangle have the same length.
View SolutionStatement I: Glucose and fructose both reduce Schiff's reagent.
Statement II: Both have free carbonyl group.
View Solution
