(a) Under what conditions is the phenomenon of total internal reflection of light observed? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
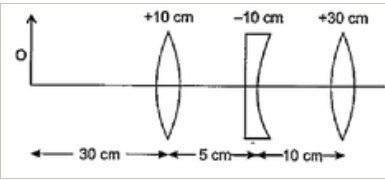
(b) Three lenses of focal lengths are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination.
(b) (i) Write a balanced equation showing nuclear fission of Uranium nucleus.
(ii) In a nuclear reactor, what is the function of :
(a) Cadmium rods? (b) Graphite rods?
(a) calculate = mass of nucleons - mass of nucleus
Binding energy = (in MeV).
(b) Learn the charateristics of X-rays and continuous X-rays.
Similar Questions
Knowledge Check
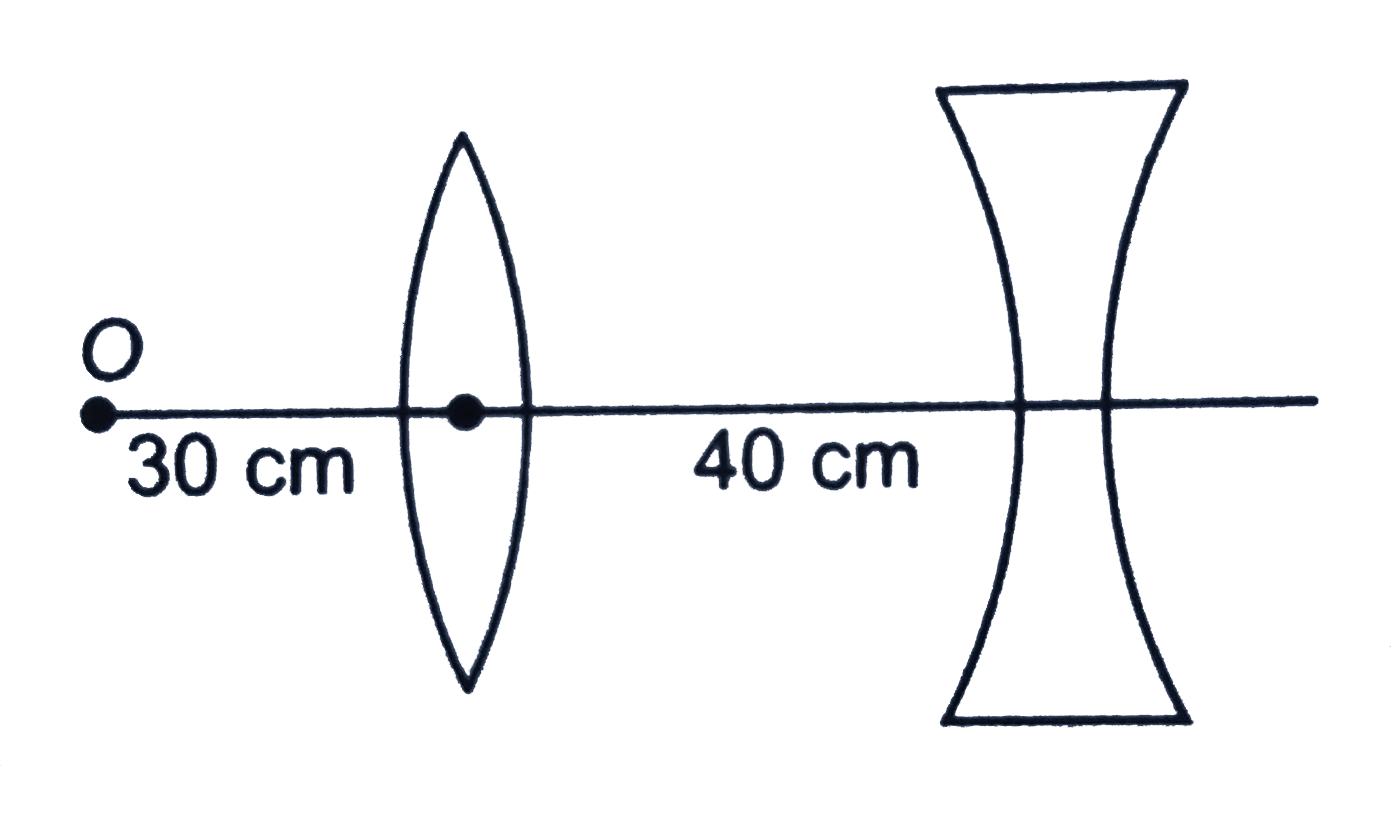
Two lenses of focal lengths 20cmand−40cm are held in contact. The image of an object at infinity will be formed by the combination at
A10cmB20cmC40 cmDinfinity
For total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionIf an observer sees the bottom of the vessel shown in Figure., at 8cm, find the refractive index of the medium in which the observer is present.

View SolutionTwo plano-convex lenses of focal lengths 20cm and 30cm are placed together to form a double convex lens. The final focal length will be
View SolutionFocal length of a convex lense in air is 20cm. and of concave lens 40cm. Find the position of final image.
View SolutionA thin equiconvex lens (μ=3/2) of focal length 10cm is cut and separated and a material of refractive index 3 is filled between them. What is the focal length of the combination?
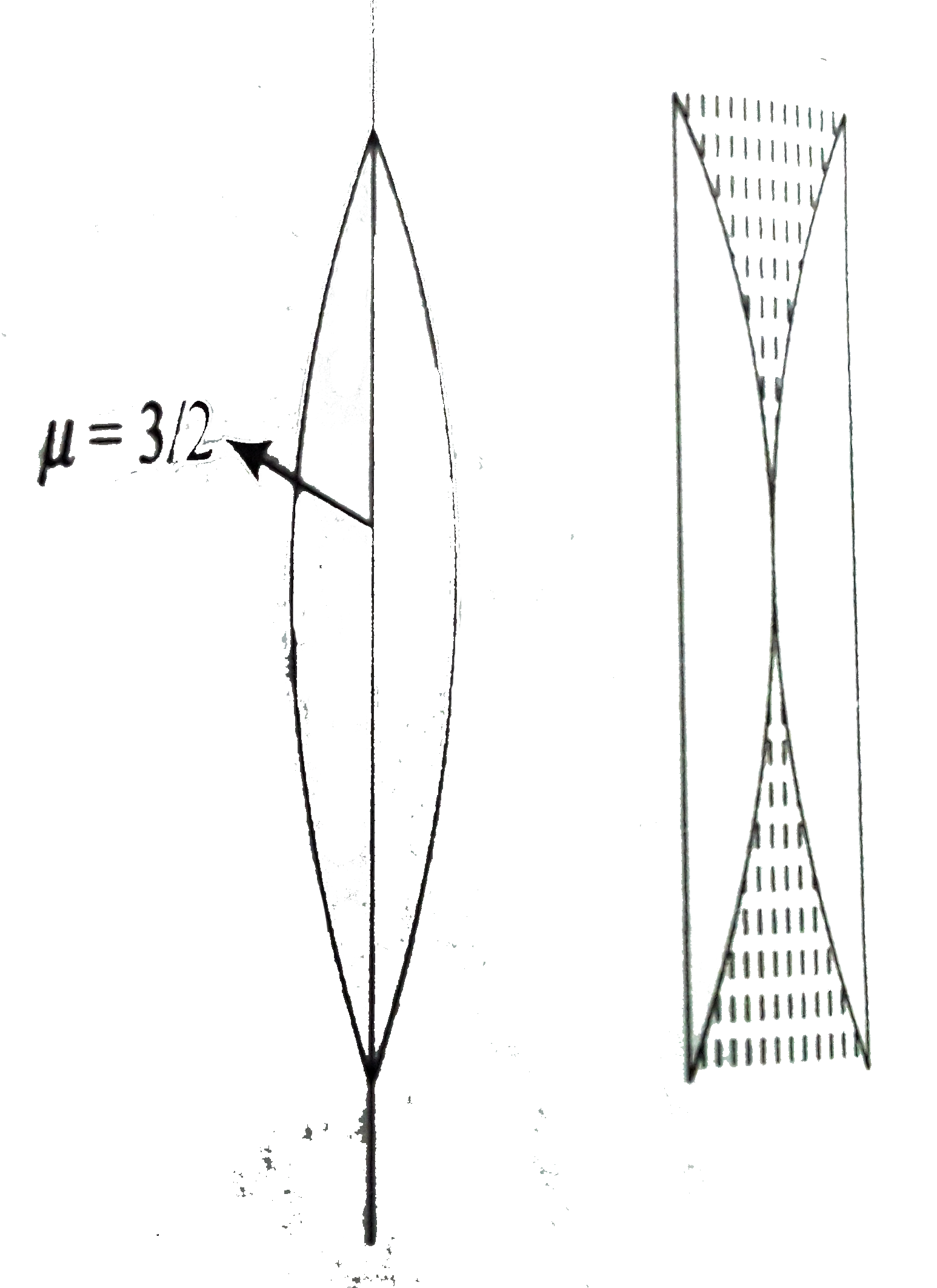
View SolutionA lens of focal length 12cm forms an upright image three times the size of a real object. Find the distance in cm between the object and image.
View SolutionAn illuminated point object O is kept 20 cm from a thin convex lens L1 of focal length 15 cm as shown below. A thin diverging lens L2 of focal length 25 cm is kept co - axial with the first lens and 35cm from it, as shown in figure below :
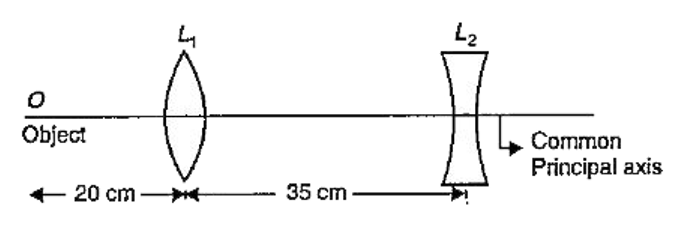
Find the position of the final image formed by this combination of lenses.
View Solution
