Two similar balls having equal positive charge q are suspanded by two insulating stings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two ?
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the Initial Setup
We have two similar balls, each carrying an equal positive charge q, suspended by insulating strings of equal length. They are separated by a distance d.
Step 2: Calculate the Initial Force
The electrostatic force F0 between the two charges in a vacuum can be calculated using Coulomb's law:
F0=14πϵ0q2d2
where ϵ0 is the permittivity of free space.
Step 3: Introduce the Plastic Sheet
When a plastic sheet is inserted between the two charged balls, the medium between them changes. The plastic sheet has a dielectric constant K (where K>1).
Step 4: Calculate the New Force with the Dielectric
The presence of the dielectric reduces the electrostatic force between the charges. The new force F can be expressed as:
F=14πϵq2d2
where ϵ (the permittivity of the medium with the dielectric) is given by:
ϵ=K⋅ϵ0
Thus, we can rewrite the force as:
F=14πKϵ0q2d2
Step 5: Relate the New Force to the Initial Force
From the above equations, we can relate the new force F to the initial force F0:
F=F0K
Since K>1, it follows that:
F<F0
Conclusion
The introduction of the plastic sheet decreases the electrostatic force between the two charged balls.
Summary of the Solution
1. Initial Force Calculation: F0=14πϵ0q2d2
2. Effect of Plastic Sheet: Introduces dielectric constant K.
3. New Force Calculation: F=F0K
4. Conclusion: The force decreases when the plastic sheet is inserted.
---
We have two similar balls, each carrying an equal positive charge q, suspended by insulating strings of equal length. They are separated by a distance d.
The electrostatic force F0 between the two charges in a vacuum can be calculated using Coulomb's law:
F0=14πϵ0q2d2
where ϵ0 is the permittivity of free space.
When a plastic sheet is inserted between the two charged balls, the medium between them changes. The plastic sheet has a dielectric constant K (where K>1).
The presence of the dielectric reduces the electrostatic force between the charges. The new force F can be expressed as:
F=14πϵq2d2
where ϵ (the permittivity of the medium with the dielectric) is given by:
ϵ=K⋅ϵ0
Thus, we can rewrite the force as:
F=14πKϵ0q2d2
From the above equations, we can relate the new force F to the initial force F0:
F=F0K
Since K>1, it follows that:
F<F0
The introduction of the plastic sheet decreases the electrostatic force between the two charged balls.
1. Initial Force Calculation: F0=14πϵ0q2d2
2. Effect of Plastic Sheet: Introduces dielectric constant K.
3. New Force Calculation: F=F0K
4. Conclusion: The force decreases when the plastic sheet is inserted.
Similar Questions
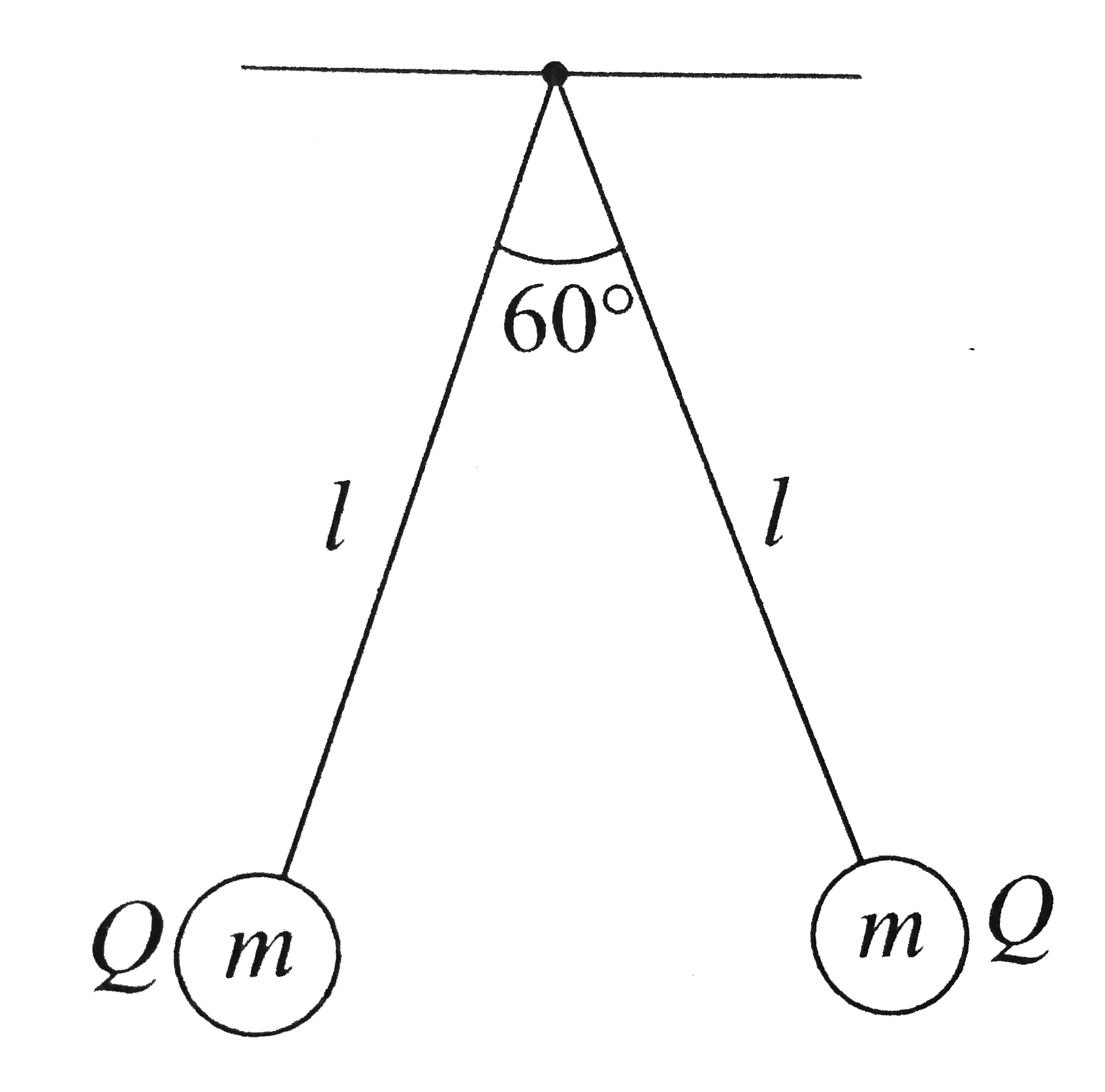
Two small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
View SolutionTwo small balls having equal positive charge Q C on each are suspended by two insulating strings of equal length L metre, from a hook fixed to a stand. The whole setup is taken into space where there is no gravity (state of weightlessness). Then the angle θ between the two strings is
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
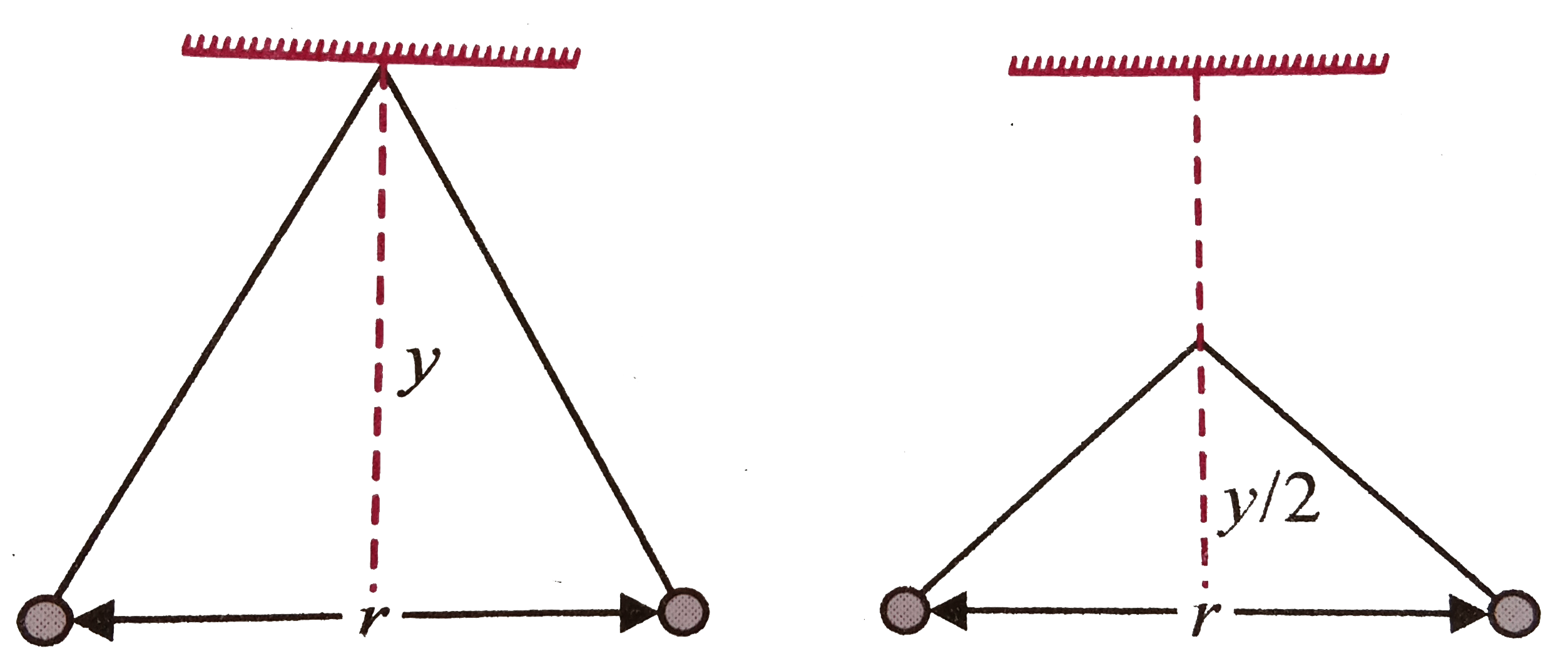
View SolutionTwo pitch balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become

View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View Solution
