Two small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
Q24π∈0L2
Q28π∈0L2
Q212π∈0L2
Q216π∈0L2
The correct Answer is:D
To solve the problem, we will analyze the forces acting on the two charged balls when they are in a state of weightlessness in space.
1. Understanding the Setup:
- We have two small balls, each with an equal positive charge Q, suspended by insulating strings of equal length L.
- The system is taken into space where there is no gravity (weightlessness).
2. Identifying Forces:
- In a gravitational field, the weight of each ball would exert a downward force mg (where m is the mass of the ball and g is the acceleration due to gravity).
- However, in the absence of gravity, the weight mg=0.
3. Electrostatic Force:
- The only force acting on the balls is the electrostatic force due to their charges.
- Since both balls have the same charge Q, they will repel each other with a force given by Coulomb's Law:
F=k⋅Q2r2
- Here, k is Coulomb's constant, r is the distance between the two charges.
4. Distance Between Charges:
- When the balls repel each other to the maximum extent, the distance r between them will be 2L (since each string has length L).
5. Calculating the Electrostatic Force:
- Substituting r=2L into the formula for electrostatic force:
F=k⋅Q2(2L)2=k⋅Q24L2
6. Tension in the Strings:
- In the state of weightlessness, the tension T in each string will equal the electrostatic force acting between the two charges:
T=k⋅Q24L2
7. Substituting the Value of k:
- The value of k is given by:
k=14πϵ0
- Therefore, substituting this into the equation for tension:
T=14πϵ0⋅Q24L2
- Simplifying this gives:
T=Q216πϵ0L2
8. Final Result:
- The tension in each string is:
T=Q216πϵ0L2
- We have two small balls, each with an equal positive charge Q, suspended by insulating strings of equal length L.
- The system is taken into space where there is no gravity (weightlessness).
- In a gravitational field, the weight of each ball would exert a downward force mg (where m is the mass of the ball and g is the acceleration due to gravity).
- However, in the absence of gravity, the weight mg=0.
- The only force acting on the balls is the electrostatic force due to their charges.
- Since both balls have the same charge Q, they will repel each other with a force given by Coulomb's Law:
F=k⋅Q2r2
- Here, k is Coulomb's constant, r is the distance between the two charges.
- When the balls repel each other to the maximum extent, the distance r between them will be 2L (since each string has length L).
- Substituting r=2L into the formula for electrostatic force:
F=k⋅Q2(2L)2=k⋅Q24L2
- In the state of weightlessness, the tension T in each string will equal the electrostatic force acting between the two charges:
T=k⋅Q24L2
- The value of k is given by:
k=14πϵ0
- Therefore, substituting this into the equation for tension:
T=14πϵ0⋅Q24L2
- Simplifying this gives:
T=Q216πϵ0L2
- The tension in each string is:
T=Q216πϵ0L2
Topper's Solved these Questions
Similar Questions
Two small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small balls having equal positive charge Q C on each are suspended by two insulating strings of equal length L metre, from a hook fixed to a stand. The whole setup is taken into space where there is no gravity (state of weightlessness). Then the angle θ between the two strings is
View SolutionTwo small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
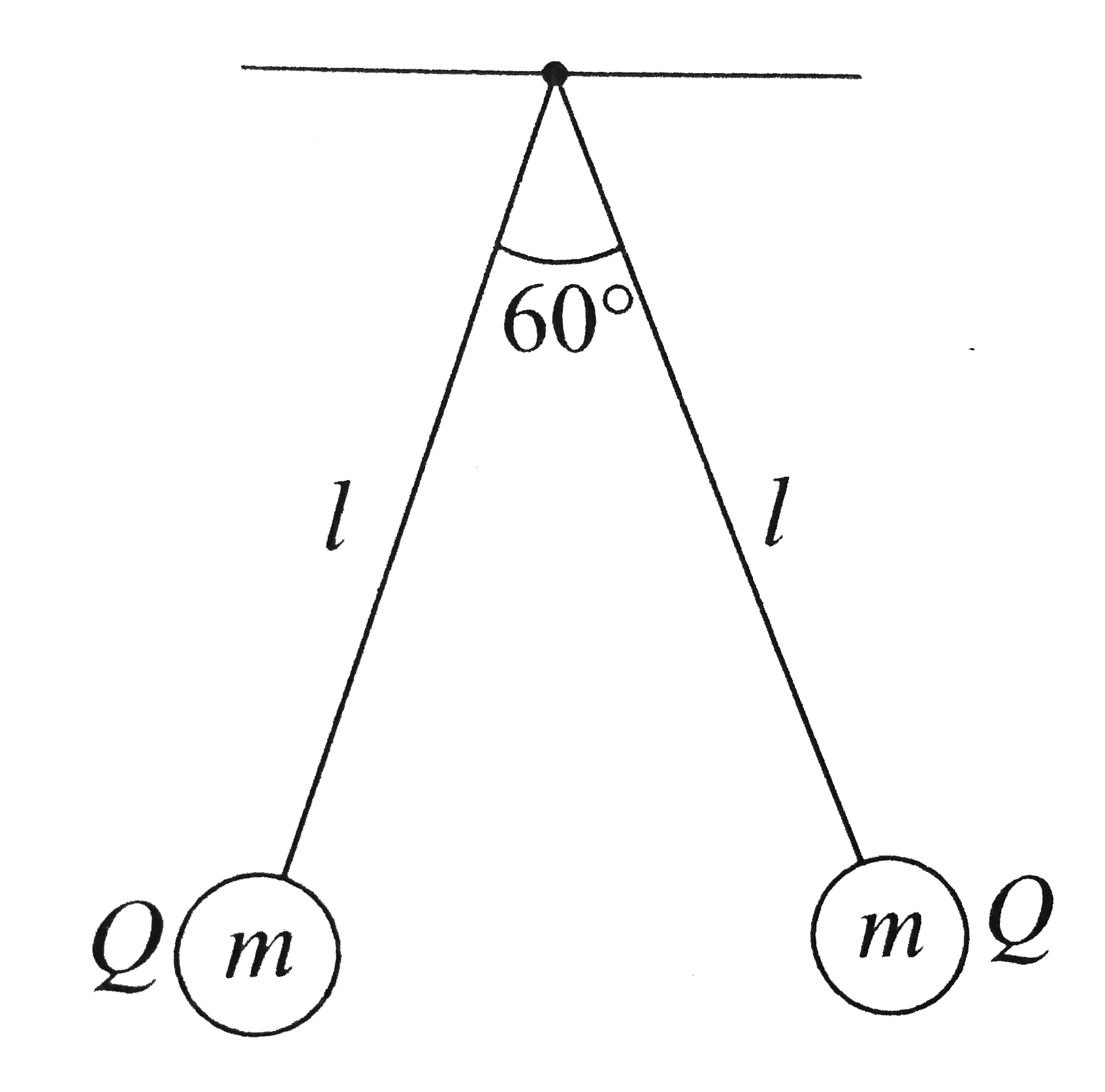 View Solution
View SolutionTwo similar balls having equal positive charge q are suspanded by two insulating stings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two ?
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View SolutionTwo small spherical balls each carrying a charge Q=10μC are suspended by two insulating threads of equal lengths 1cm each, from a point fixed in the ceiling. It is found that in equilibrium threads are sepreated by an angle 60∘ between them, as shown in figure. What is the tension in the threads
(Given 14πε0=9×109Nm/C2 )
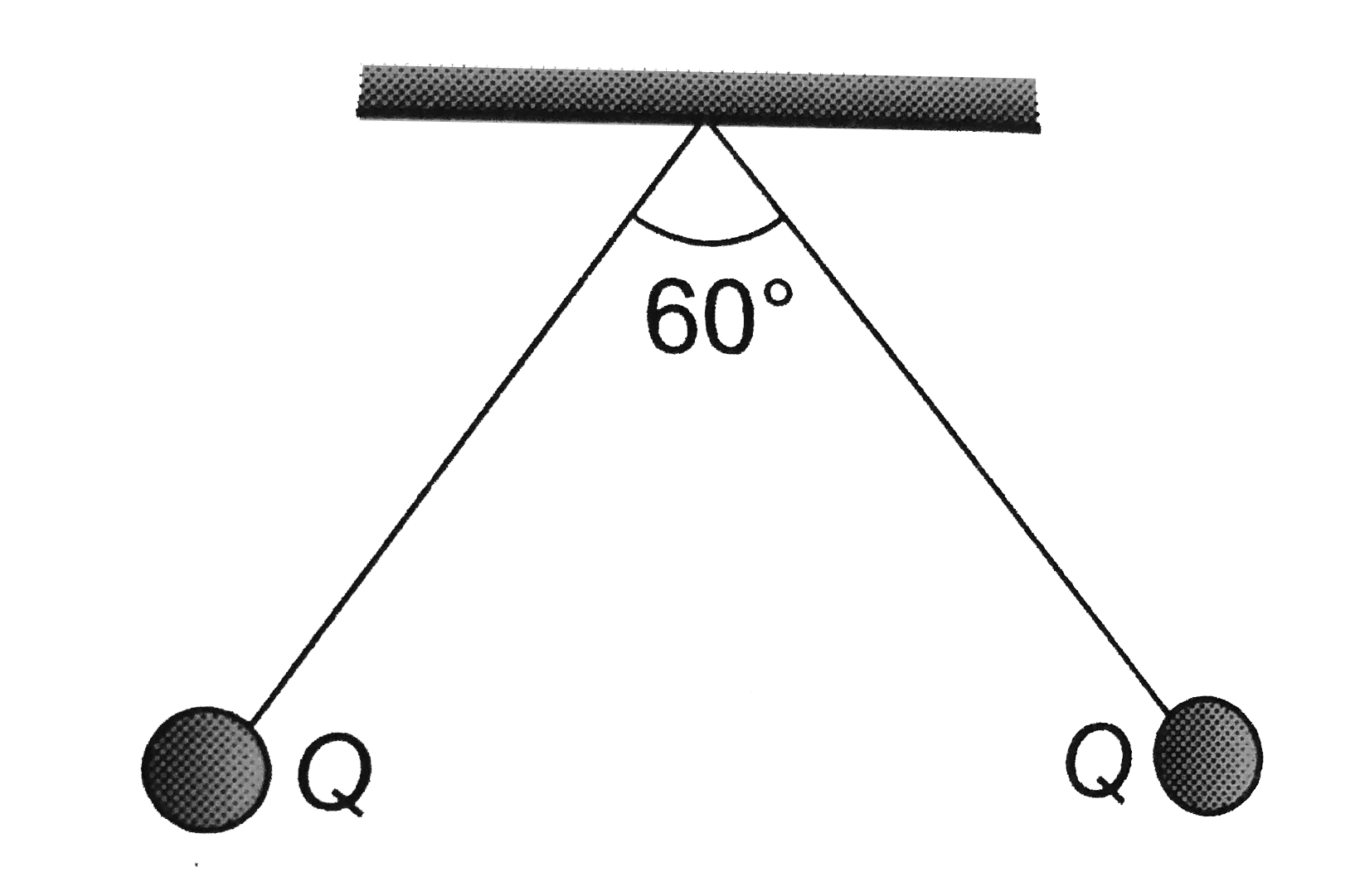 View Solution
View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
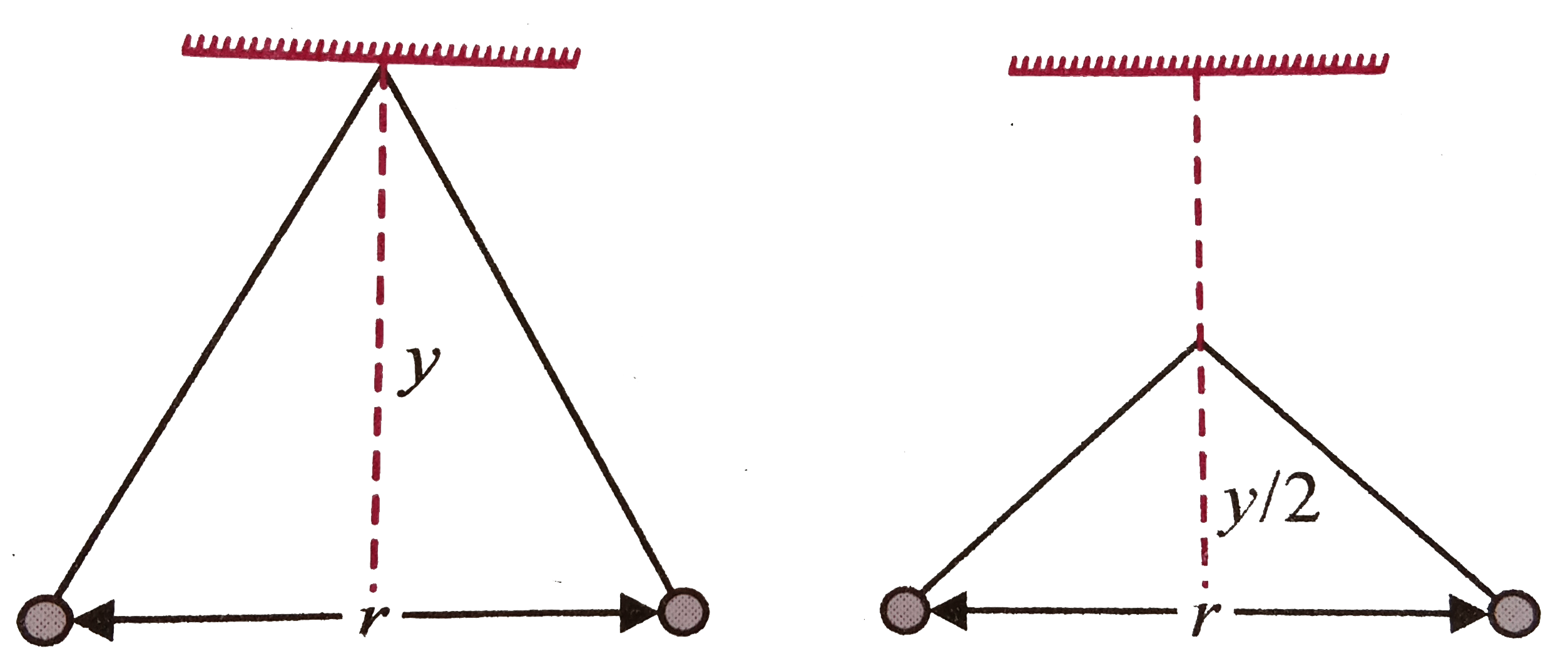 View Solution
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo charged particles having charge 2.0×10−8C. Each are joined by an isolating string of length 1m and the system is kept on a smooth horizontal task. The tension in the string.
View Solution

