When a lens of power P (in air) made of material of refractive index μ is immersed in liquid of refractive index μ0 Then the power of lens is:
μ−1μ−μ0P
μ−μ0μ−1P
μ−μ0μ−1. Pμ0
none of these
The correct Answer is:c
To solve the problem of finding the power of a lens when it is immersed in a liquid, we can follow these steps:
Step 1: Understand the Lens Maker's Formula
The lens maker's formula for a lens in air is given by:
1F=(μ−1)(1R1−1R2)
Where:
- F is the focal length of the lens.
- μ is the refractive index of the lens material.
- R1 and R2 are the radii of curvature of the lens surfaces.
Step 2: Calculate the Power of the Lens in Air
The power P of the lens is defined as:
P=1F
When the lens is in air (where the refractive index of air is approximately 1), we can express the power as:
P=(μ−1)(1R1−1R2)
Step 3: Calculate the Power of the Lens in Liquid
When the lens is immersed in a liquid with a refractive index μ0, the lens maker's formula modifies to:
1F′=(μμ0−1)(1R1−1R2)
Here, F′ is the new focal length of the lens in the liquid.
Step 4: Express the New Power of the Lens
The new power P′ of the lens in the liquid can be expressed as:
P′=1F′=(μμ0−1)(1R1−1R2)
Step 5: Relate the Two Powers
To relate the two powers P and P′, we can divide the equations for P′ and P:
P′P=(μμ0−1)(μ−1)
Rearranging gives:
P′=P⋅(μμ0−1)(μ−1)
Step 6: Substitute and Simplify
Substituting μμ0−1=μ−μ0μ0:
P′=P⋅(μ−μ0μ0)(μ−1)
This simplifies to:
P′=P⋅μ−μ0μ−1⋅1μ0
Final Result
Thus, the power of the lens when immersed in a liquid is given by:
P′=(μ−μ0)(μ−1)⋅μ0⋅P
The lens maker's formula for a lens in air is given by:
1F=(μ−1)(1R1−1R2)
Where:
- F is the focal length of the lens.
- μ is the refractive index of the lens material.
- R1 and R2 are the radii of curvature of the lens surfaces.
The power P of the lens is defined as:
P=1F
When the lens is in air (where the refractive index of air is approximately 1), we can express the power as:
P=(μ−1)(1R1−1R2)
When the lens is immersed in a liquid with a refractive index μ0, the lens maker's formula modifies to:
1F′=(μμ0−1)(1R1−1R2)
Here, F′ is the new focal length of the lens in the liquid.
The new power P′ of the lens in the liquid can be expressed as:
P′=1F′=(μμ0−1)(1R1−1R2)
To relate the two powers P and P′, we can divide the equations for P′ and P:
P′P=(μμ0−1)(μ−1)
Rearranging gives:
P′=P⋅(μμ0−1)(μ−1)
Substituting μμ0−1=μ−μ0μ0:
P′=P⋅(μ−μ0μ0)(μ−1)
This simplifies to:
P′=P⋅μ−μ0μ−1⋅1μ0
Thus, the power of the lens when immersed in a liquid is given by:
P′=(μ−μ0)(μ−1)⋅μ0⋅P
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
80 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
A double convex lens of refractive index m1 is immersed in a liquid of refractive index m2. This lens will act as:
View SolutionA converging lens has a focal length of 20cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, what will be its new foacl length ?
View Solution
Knowledge Check
A double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to
 Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
A transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
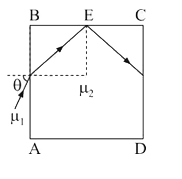
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View SolutionA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View SolutionA lens is made of flint glass (refractive index =1.5). When the lens is immersed in a liquid of refractive index 1.25 , the focal length:
View SolutionA biconcave lens made of a transparent material of refractive index 1.5 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason.
View Solution