Show that Irms=I0√2, where Irms is the root mean square value of alternating current and I0 the peak value.
Video Solution
Text Solution
Let the alternating current is I=I0sinωt
Mean square value of current,
I2=1T∫T0I2dt for a complete cycle
=1T∫T0I20sin2ωtdt=I20T∫T0(1−cos2ωt2)dt
=I202T[t−sin2ωt2ω]T0=I202T[T−0]=I202
Now by taking roots of mean square value of current
i.e, Irun=√I2=√I20/2=I0√2
where, Irms = root of mean square value,
I0 = peak value of current.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In the circuit shown, the value of currents I1,I2andI3 are
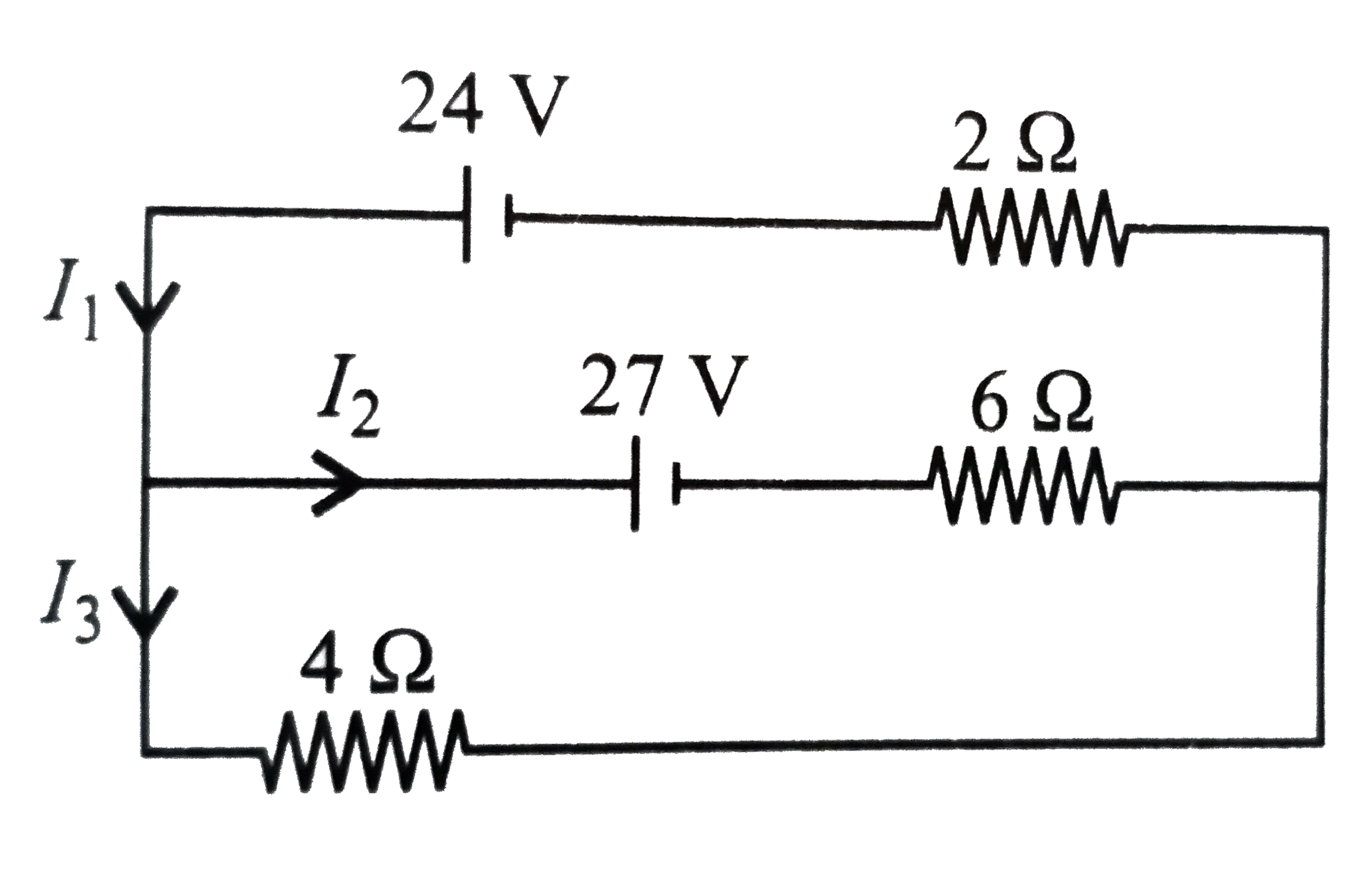 A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A - Question 2 - Select One
The rms value of current in an ac circuit is 25 A, then peak current is
A35.36mAB35.36AC3.536AD49.38A
The peak value of an alternating current is 10. A. Find its rms value
View SolutionThe peak value of Alternating current is 6amp, then r.m.s. value of current will be
View SolutionThe average value of alternating current I=I0sinωt in time interval [0,πω] is
View SolutionIf a=1+i√2, where i=√−1, then find the value of a1929.
View SolutionIf i=t2,0<t<T then r.m.s. value of current is
View SolutionIn an AC circuit, the rms value of the current Irms is related to the peak current I0 as
View Solution

