Which modulus determines the stretching of a coiled spring?
To determine which modulus governs the stretching of a coiled spring, we can follow these steps:
Step 1: Understand the Concept of Elasticity
Elasticity is the property of materials to return to their original shape after being deformed. When a force is applied to a material, it can either stretch, compress, or shear.
Hint: Elasticity is crucial for understanding how materials respond to forces.
Step 2: Identify the Relevant Moduli
There are several types of moduli in elasticity, including:
- Young's Modulus (tensile stress)
- Shear Modulus (rigidity)
- Bulk Modulus (volumetric stress)
Hint: Each modulus relates to a different type of deformation.
Step 3: Relate Modulus to the Type of Deformation
For a coiled spring, the deformation primarily involves twisting and stretching. The relevant modulus for this type of deformation is the shear modulus, also known as the modulus of rigidity.
Hint: Think about how a coiled spring behaves under tension or compression.
Step 4: Define Shear Modulus
The shear modulus (G) is defined as the ratio of shear stress to shear strain. It quantifies how much a material will deform under shear stress.
Hint: Remember that shear stress is the force applied parallel to the surface, while shear strain is the deformation resulting from that stress.
Step 5: Conclude the Answer
Since the stretching of a coiled spring is primarily determined by its ability to resist shear deformation, the modulus that determines the stretching of a coiled spring is the shear modulus.
Hint: Focus on how the spring's structure allows it to stretch and return to its original shape.
Final Answer
The modulus that determines the stretching of a coiled spring is the shear modulus (modulus of rigidity).
---
Elasticity is the property of materials to return to their original shape after being deformed. When a force is applied to a material, it can either stretch, compress, or shear.
There are several types of moduli in elasticity, including:
- Young's Modulus (tensile stress)
- Shear Modulus (rigidity)
- Bulk Modulus (volumetric stress)
For a coiled spring, the deformation primarily involves twisting and stretching. The relevant modulus for this type of deformation is the shear modulus, also known as the modulus of rigidity.
The shear modulus (G) is defined as the ratio of shear stress to shear strain. It quantifies how much a material will deform under shear stress.
Since the stretching of a coiled spring is primarily determined by its ability to resist shear deformation, the modulus that determines the stretching of a coiled spring is the shear modulus.
The modulus that determines the stretching of a coiled spring is the shear modulus (modulus of rigidity).
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)LONG ANSWER QUESTIONS
5 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)SHORT ANSWER QUESTIONS
20 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)
2 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
Read each of the statement below carefully and state, with reasons, if it is true or false.
(a) The modulus of elasticity of rubber is greater than that of steel.
(b) the stretching of a coil is determined by its shear modulus.
View SolutionA small trolley of mass 2.0 kg resting on a horizontal turntable is connected by a light spring to the centre of the table. When the turntable is set into rotation at a speed of 300 rev/min the length of the stretched spring is 40 cm. If the original length of the spring is 35 cm, determine the force constant of the spring.
View SolutionWhich type of strain is there, when a spiral spring is stretched by a force?
View SolutionA long spring when stretched by xcm, has a potential energy U. On increasing the stretching to nxcm, the potential energy stored in spring will be
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
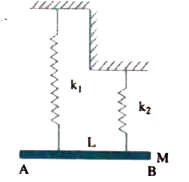
View SolutionA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png)
View SolutionA spring 40 mm long is stretched by the application of a force. If 10 N force required to stretch the spring through 1mm, then the work done in stretching the spring through 40 mm is
View SolutionTwo springs have their force constants in the ratio of 3:4. Both the springs are stretched by applying equal force F. If elongation in first spring is x then elogation is second spring is
View SolutionA heavy weight is suspended from a spring . A person raises the weight till the spring becomes slack . The done by him is W. The energy stored in the stretched spring was E . What will be the gain in gravitational potential energy?
View SolutionThe potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:-
View Solution
