Define stress, strain and Young's modulus of an elastic material. Describe an experiment for measuring the Young's modulus of a material in the form of a wire.
Step-by-Step Solution
Step 1: Define Stress
Stress is defined as the internal resistance offered by a material when subjected to an external force. It is mathematically expressed as:
Stress(σ)=FA
where F is the applied force and A is the cross-sectional area of the material. The unit of stress is Pascal (Pa).
Step 2: Define Strain
Strain is a measure of deformation representing the displacement between particles in a material body. It is defined as the ratio of the change in length to the original length of the material:
Strain(ϵ)=ΔLL
where ΔL is the change in length and L is the original length. Strain is a dimensionless quantity.
Step 3: Define Young's Modulus
Young's modulus (E) is a measure of the stiffness of an elastic material. It is defined as the ratio of stress to strain:
E=σϵ
Substituting the definitions of stress and strain, we get:
E=F/AΔL/L=F⋅LA⋅ΔL
The unit of Young's modulus is also Pascal (Pa).
Step 4: Describe the Experiment to Measure Young's Modulus
To measure Young's modulus of a material in the form of a wire, we can perform a tensile test. The steps are as follows:
1. Setup: Take a uniform wire of known length (L) and cross-sectional area (A). Attach one end of the wire to a fixed support and the other end to a weight hanger.
2. Apply Force: Gradually add known weights (F) to the weight hanger. Record the corresponding elongation (ΔL) of the wire for each weight applied.
3. Measure Changes: For each weight added, measure the change in length of the wire. This can be done using a ruler or a vernier caliper.
4. Calculate Stress and Strain:
- Calculate stress for each weight using σ=FA.
- Calculate strain using ϵ=ΔLL.
5. Plot the Graph: Plot a graph of stress (y-axis) versus strain (x-axis). The slope of the linear portion of the graph gives Young's modulus (E).
6. Calculate Young's Modulus: Use the formula:
E=F⋅LA⋅ΔL
to calculate Young's modulus for the wire.
Stress is defined as the internal resistance offered by a material when subjected to an external force. It is mathematically expressed as:
Stress(σ)=FA
where F is the applied force and A is the cross-sectional area of the material. The unit of stress is Pascal (Pa).
Strain is a measure of deformation representing the displacement between particles in a material body. It is defined as the ratio of the change in length to the original length of the material:
Strain(ϵ)=ΔLL
where ΔL is the change in length and L is the original length. Strain is a dimensionless quantity.
Young's modulus (E) is a measure of the stiffness of an elastic material. It is defined as the ratio of stress to strain:
E=σϵ
Substituting the definitions of stress and strain, we get:
E=F/AΔL/L=F⋅LA⋅ΔL
The unit of Young's modulus is also Pascal (Pa).
To measure Young's modulus of a material in the form of a wire, we can perform a tensile test. The steps are as follows:
- Calculate stress for each weight using σ=FA.
- Calculate strain using ϵ=ΔLL.
E=F⋅LA⋅ΔL
to calculate Young's modulus for the wire.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)SHORT ANSWER QUESTIONS
20 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)VERY SHORT ANSWER QUESTIONS
8 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
Knowledge Check
Young's modulus of a wire depends on
Adiameter of the wireBmass hanging from the wireClength of the wireDÂ material of the wire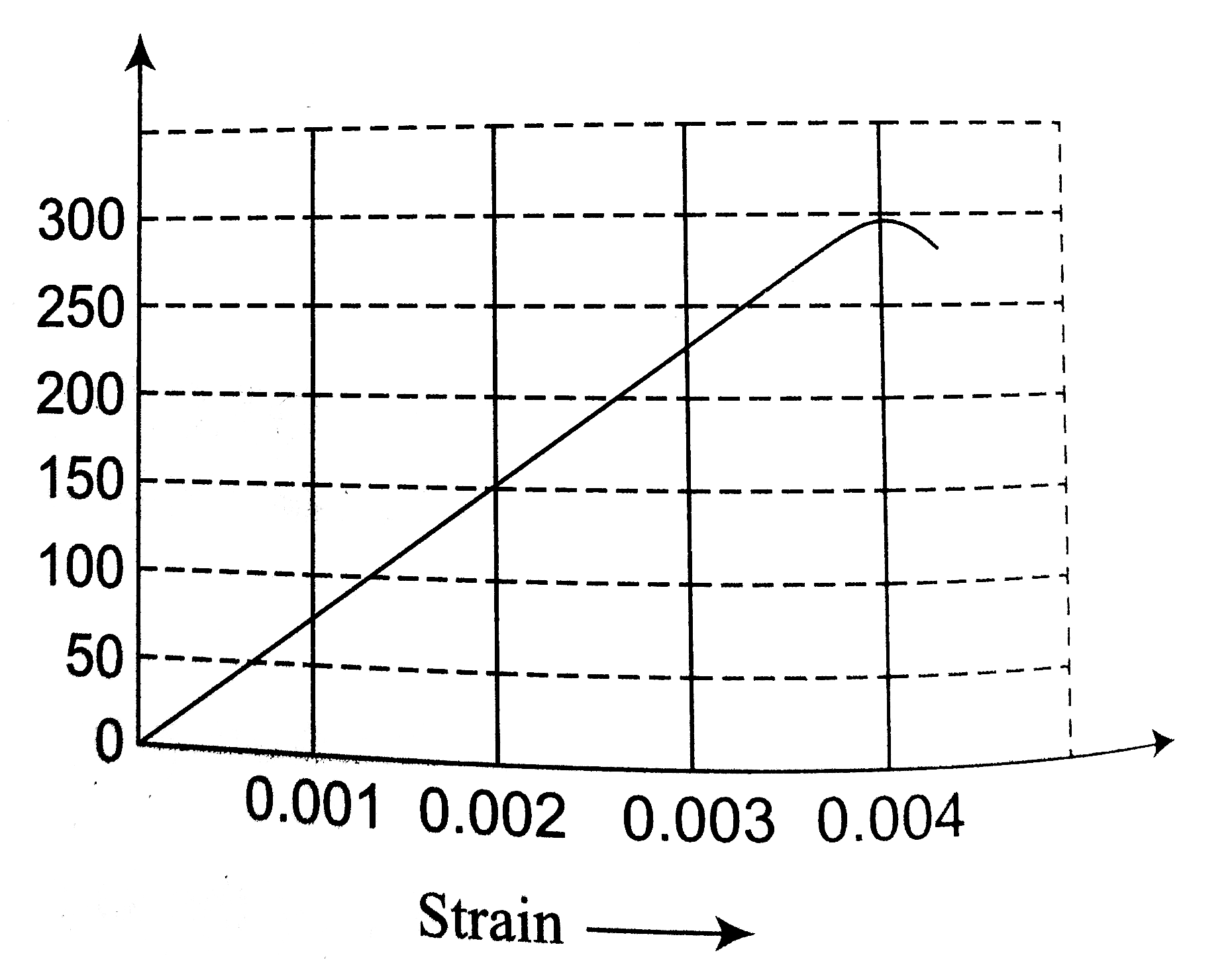
Figure shows the strain stress curve for a given material. The Young's modulus of the material isA5×109Nm−2B5×1010Nm−2C7.5×109Nm−2D7.5×1010Nm−2
With a rise of temperature, the Young’s modulus :
View SolutionYoung modulus of elasticity for a gas is
View SolutionFind the dimensions of stress, strain and modulus of elasticity.
View SolutionThe Young's modulus of a wire is numerically equal
View SolutionYoung's modulus for a perfectly rigid body is
View SolutionThe dimensional formula for young's modulus is
View Solution