The ride is circus rides along a circular track in a vertical plane. The minimum velocity at the highest point of the track will be
√(2gR)
√(5gR)
√(3gR)
√(gR)
The correct Answer is:d
To find the minimum velocity at the highest point of a circular track in a vertical plane, we can analyze the forces acting on the object at that point.
1. Identify Forces at the Highest Point:
At the highest point of the circular track, the forces acting on the object are:
- The gravitational force (weight) acting downwards: Fg=mg
- The centripetal force required to keep the object moving in a circular path, which is provided by the gravitational force at this point.
2. Centripetal Force Requirement:
The centripetal force needed to keep the object moving in a circular path is given by the formula:
Fc=mv2r
where:
- m is the mass of the object,
- v is the velocity at the highest point,
- r is the radius of the circular path.
3. Setting Forces Equal:
At the highest point, the gravitational force must provide the necessary centripetal force. Therefore, we set the two forces equal:
mg=mv2r
4. Cancel Mass:
Since m appears on both sides of the equation, we can cancel it out (assuming m≠0):
g=v2r
5. Rearranging the Equation:
To find the minimum velocity v at the highest point, we rearrange the equation:
v2=gr
Taking the square root of both sides gives:
v=√gr
Final Answer:
The minimum velocity at the highest point of the track is:
v=√gr
At the highest point of the circular track, the forces acting on the object are:
- The gravitational force (weight) acting downwards: Fg=mg
- The centripetal force required to keep the object moving in a circular path, which is provided by the gravitational force at this point.
The centripetal force needed to keep the object moving in a circular path is given by the formula:
Fc=mv2r
where:
- m is the mass of the object,
- v is the velocity at the highest point,
- r is the radius of the circular path.
At the highest point, the gravitational force must provide the necessary centripetal force. Therefore, we set the two forces equal:
mg=mv2r
Since m appears on both sides of the equation, we can cancel it out (assuming m≠0):
g=v2r
To find the minimum velocity v at the highest point, we rearrange the equation:
v2=gr
Taking the square root of both sides gives:
v=√gr
The minimum velocity at the highest point of the track is:
v=√gr
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION (ROTATIONAL MOTION AND MOMENT OF INERTIA )25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - GRAVITATION25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - MOTION IN FLUIDS25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
A player throws a ball vertically upwards with velocity u. At highest point,
A1. both the velocity and acceleration of the ball are zero.B2. the velocity of the ball is u but its accelerationC3. the velocity of the ball is zero but its acceleration is g.D4. the velocity of the ball is u but its acceleration is g. - Question 2 - Select One
A small block is shot into each of the four track as shown in Fig 15.7.1. Each of the track rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
A B
B C
C D
D
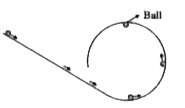
A ball of mass 100 g is made to loop-the-loop in a vertical circle as shown in Fig. 7.1.29. The radius of the circle is 0.5 m (i)-What is the critical velocity at the highest point of the track ? (ii) If the velocity of the ball at the highest point of the track is twice the critical velocity what is the force exerted by the ball against track?
 View Solution
View SolutionA particle tied to a string moves in a circular path in vertical plane. Its velocity at lowerst point is such that it just completes circle. Find the ratio of resultant force on particle at the lowerst point to that at highest point.
View SolutionA particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
View SolutionIs a train moving on a circular track, an inertial frame of reference ?
View SolutionA toy train moving around a circular track has rotatory motion.
View SolutionThe projectile has only vertical component of velocity at the highest point of its trajectory.
At the highest point, only one component of velocity is present.View Solution

